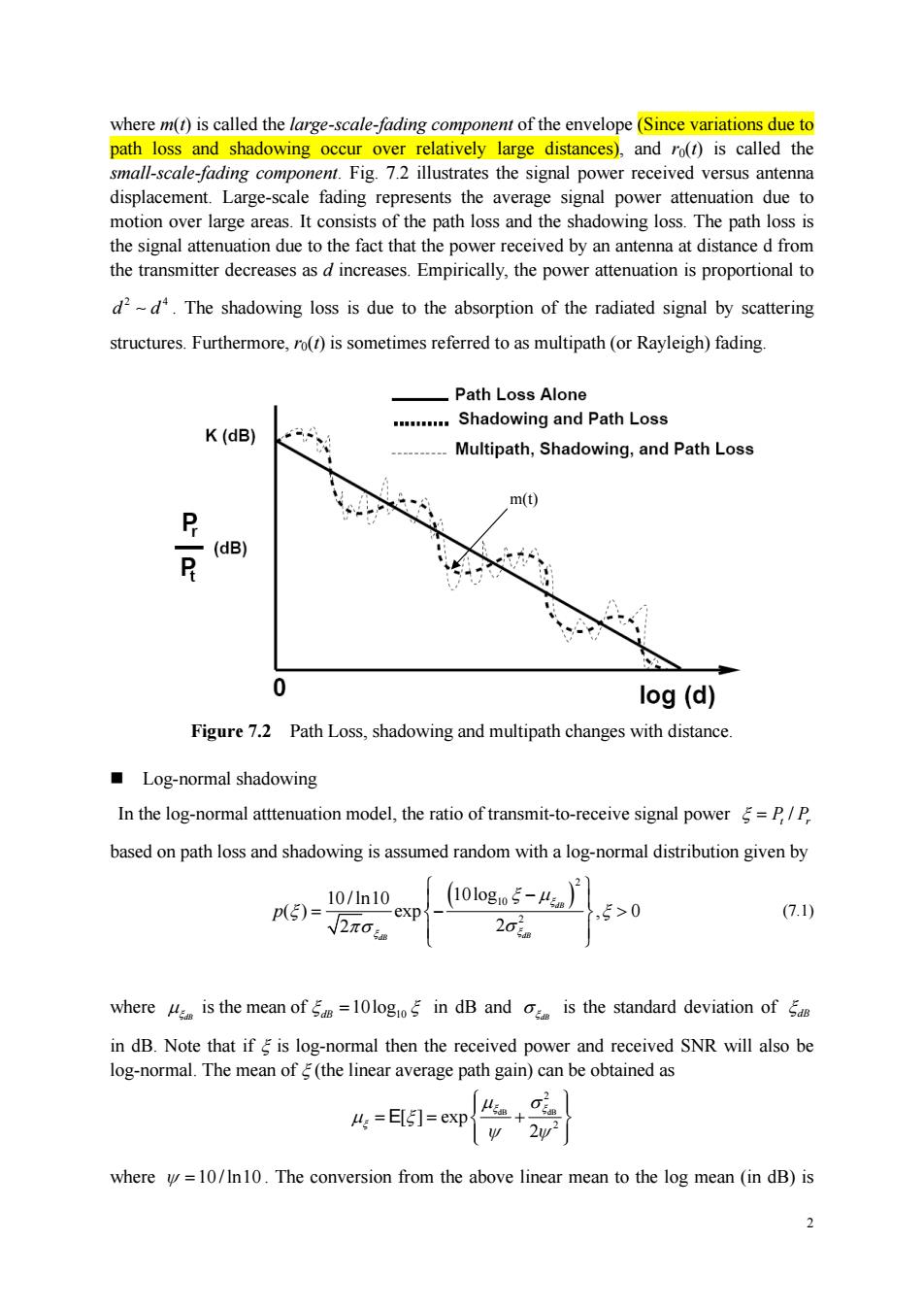
where m(t)is called the large-scale-fading component of the envelope(Since variations due to path loss and shadowing oc arge distances) and ro(t)is called the mall-scale-fadi ng component.Fig 72 illustrates the signal power received versus antenna displacement.Large-scale fading represents the average signal power attenuation due to motion over large areas.It consists of the path loss and the shadowing loss.The path loss is the signal attenuation due to the fact that the power received by an antenna at distance d from the transmitter decreases as d increases.Empirically,the power attenuation is proportional to d2-d.The shadowing loss is due to the absorption of the radiated signal by scattering structures.Furthermore,ro(r)is sometimes referred to as multipath(or Rayleigh)fading. Path Loss Alone .Shadowing and Path Loss K(dB) Multipath,Shadowing,and Path Loss m(0 公 (dB) 0 log (d) Figure 7.2 Path Loss,shadowing and multipath changes with distance. Log-normal shadowing In the log-normal atttenuation model,the ratio of transmit-to-receive signal power=P/P based on path loss and shadowing is assumed random with a log-normal distribution given by Pp(53=10/1n10 XD _(10g5-4l ,5>0 (7.1) where is the mean of=10log in dB and is the standard deviation of in dB.Note that if is log-normal then the received power and received SNR will also be log-normal.The mean of(the linear average path gain)can be btain where =10/In10.The conversion from the above linear mean to the log mean (in dB)is2 where m(t) is called the large-scale-fading component of the envelope (Since variations due to path loss and shadowing occur over relatively large distances), and r0(t) is called the small-scale-fading component. Fig. 7.2 illustrates the signal power received versus antenna displacement. Large-scale fading represents the average signal power attenuation due to motion over large areas. It consists of the path loss and the shadowing loss. The path loss is the signal attenuation due to the fact that the power received by an antenna at distance d from the transmitter decreases as d increases. Empirically, the power attenuation is proportional to 2 4 d d  . The shadowing loss is due to the absorption of the radiated signal by scattering structures. Furthermore, r0(t) is sometimes referred to as multipath (or Rayleigh) fading. Figure 7.2 Path Loss, shadowing and multipath changes with distance.  Log-normal shadowing In the log-normal atttenuation model, the ratio of transmit-to-receive signal power / P P t r   based on path loss and shadowing is assumed random with a log-normal distribution given by   2 10 2 10 / ln10 10log ( ) exp , 0 2 2 dB dB dB p                       (7.1) where 10 is the mean of 10log dB  dB    in dB and dB   is the standard deviation of dB  in dB. Note that if  is log-normal then the received power and received SNR will also be log-normal. The mean of  (the linear average path gain) can be obtained as dB dB 2 2 [ ] exp 2                    E where  10 / ln10 . The conversion from the above linear mean to the log mean (in dB) is m(t)