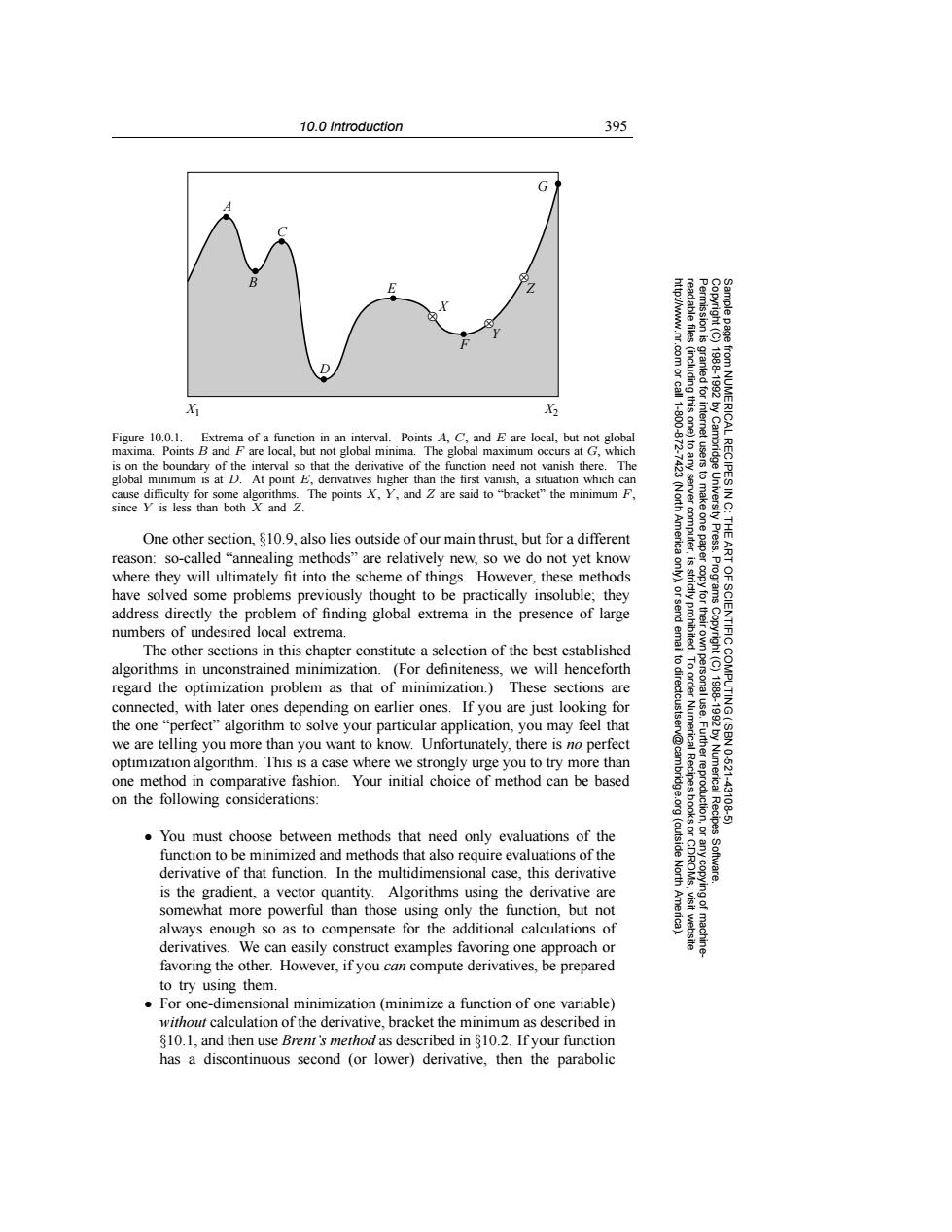
10.0 Introduction 395 G Z .com or call 19881992 3 11100 Figure 10.0.1.Extrema of a function in an interval.Points A,C,and E are local,but not global maxima.Points B and F are local,but not global minima.The global maximum occurs at G,which is on the boundary of the interval so that the derivative of the function need not vanish there.The global minimum is at D.At point E,derivatives higher than the first vanish,a situation which can server from NUMERICAL RECIPES IN C: cause difficulty for some algorithms.The points X,Y,and Z are said to "bracket"the minimum F, since Y is less than both X and Z. (Nort One other section,$10.9,also lies outside of our main thrust,but for a different America computer, UnN电.t reason:so-called "annealing methods"are relatively new,so we do not yet know where they will ultimately fit into the scheme of things.However,these methods have solved some problems previously thought to be practically insoluble;they address directly the problem of finding global extrema in the presence of large numbers of undesired local extrema. The other sections in this chapter constitute a selection of the best established algorithms in unconstrained minimization.(For definiteness,we will henceforth 可 regard the optimization problem as that of minimization.)These sections are connected,with later ones depending on earlier ones.If you are just looking for the one"perfect"algorithm to solve your particular application,you may feel that we are telling you more than you want to know.Unfortunately,there is no perfect optimization algorithm.This is a case where we strongly urge you to try more than one method in comparative fashion.Your initial choice of method can be based on the following considerations: Fuurrggroglrion Numerical Recipes 10-621 43106 You must choose between methods that need only evaluations of the (outside function to be minimized and methods that also require evaluations of the derivative of that function.In the multidimensional case,this derivative Software. is the gradient,a vector quantity.Algorithms using the derivative are ying of somewhat more powerful than those using only the function,but not always enough so as to compensate for the additional calculations of derivatives.We can easily construct examples favoring one approach or favoring the other.However,if you can compute derivatives,be prepared to try using them. For one-dimensional minimization (minimize a function of one variable) without calculation of the derivative,bracket the minimum as described in 810.1,and then use Brent's method as described in $10.2.If your function has a discontinuous second (or lower)derivative,then the parabolic10.0 Introduction 395 Permission is granted for internet users to make one paper copy for their own personal use. Further reproduction, or any copyin Copyright (C) 1988-1992 by Cambridge University Press. Programs Copyright (C) 1988-1992 by Numerical Recipes Software. Sample page from NUMERICAL RECIPES IN C: THE ART OF SCIENTIFIC COMPUTING (ISBN 0-521-43108-5) g of machine￾readable files (including this one) to any server computer, is strictly prohibited. To order Numerical Recipes books or CDROMs, visit website http://www.nr.com or call 1-800-872-7423 (North America only), or send email to directcustserv@cambridge.org (outside North America). G Z Y F X E D B A C X1 X2 ⊗ ⊗ ⊗ Figure 10.0.1. Extrema of a function in an interval. Points A, C, and E are local, but not global maxima. Points B and F are local, but not global minima. The global maximum occurs at G, which is on the boundary of the interval so that the derivative of the function need not vanish there. The global minimum is at D. At point E, derivatives higher than the first vanish, a situation which can cause difficulty for some algorithms. The points X, Y , and Z are said to “bracket” the minimum F, since Y is less than both X and Z. One other section, §10.9, also lies outside of our main thrust, but for a different reason: so-called “annealing methods” are relatively new, so we do not yet know where they will ultimately fit into the scheme of things. However, these methods have solved some problems previously thought to be practically insoluble; they address directly the problem of finding global extrema in the presence of large numbers of undesired local extrema. The other sections in this chapter constitute a selection of the best established algorithms in unconstrained minimization. (For definiteness, we will henceforth regard the optimization problem as that of minimization.) These sections are connected, with later ones depending on earlier ones. If you are just looking for the one “perfect” algorithm to solve your particular application, you may feel that we are telling you more than you want to know. Unfortunately, there is no perfect optimization algorithm. This is a case where we strongly urge you to try more than one method in comparative fashion. Your initial choice of method can be based on the following considerations: • You must choose between methods that need only evaluations of the function to be minimized and methods that also require evaluations of the derivative of that function. In the multidimensional case, this derivative is the gradient, a vector quantity. Algorithms using the derivative are somewhat more powerful than those using only the function, but not always enough so as to compensate for the additional calculations of derivatives. We can easily construct examples favoring one approach or favoring the other. However, if you can compute derivatives, be prepared to try using them. • For one-dimensional minimization (minimize a function of one variable) without calculation of the derivative, bracket the minimum as described in §10.1, and then use Brent’s method as described in §10.2. If your function has a discontinuous second (or lower) derivative, then the parabolic