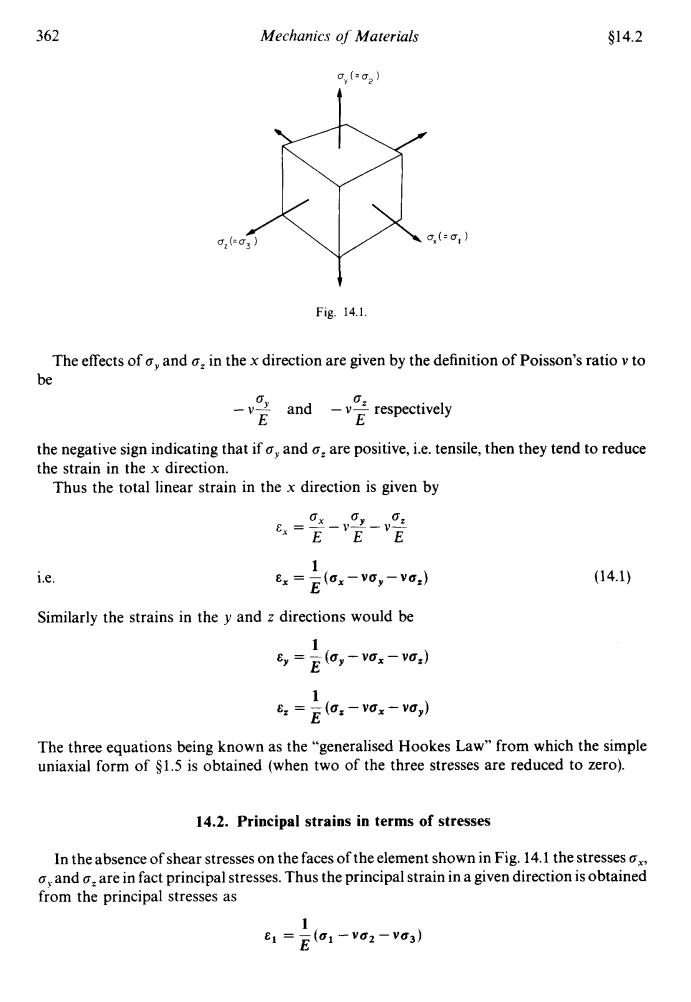
362 Mechanics of Materials S14.2 c(=g2） g,(=g,) Fig.14.1. The effects of and in the x direction are given by the definition of Poisson's ratio v to be and respectively E the negative sign indicating that if a,and o:are positive,i.e.tensile,then they tend to reduce the strain in the x direction. Thus the total linear strain in the x direction is given by 6-2--呢 1 i.e. 6x=E(ox-vo,-vo;) (14.1) Similarly the strains in the y and z directions would be 1 ,=Eo,-vox-vo,） 1 e:=E(:-vo,-vo,) The three equations being known as the "generalised Hookes Law"from which the simple uniaxial form of $1.5 is obtained (when two of the three stresses are reduced to zero). 14.2.Principal strains in terms of stresses In the absence of shear stresses on the faces of the element shown in Fig.14.1 the stresses ox o and o.are in fact principal stresses.Thus the principal strain in a given direction is obtained from the principal stresses as 1 6 =E(01-vo2-va3)362 Mechankr oj Materials g14.2 t Fig. 14.1 The effects of Q, and cZ in the x direction are given by the definition of Poisson’s ratio v to be Q 0 - v2 and - vP respectively E E the negative sign indicating that if Q, and Q, are positive, i.e. tensile, then they tend to reduce the strain in the x direction. Thus the total linear strain in the x direction is given by E, = -((6,-VfJy-V~,) 1 E Le. (14.1) Similarly the strains in the y and z directions would be 1 E E, = - (Qy - vox - va,) E, = -(a, 1 - vox - YOy) E The three equations being known as the “generalised Hookes Law” from which the simple uniaxial form of $1.5 is obtained (when two of the three stresses are reduced to zero). 14.2. Principal strains in terms of stresses In the absence of shear stresses on the faces of the element shown in Fig. 14.1 the stresses ox, CJ) and Q, are in fact principal stresses. Thus the principal strain in a given direction is obtained from the principal stresses as 1 E E1 = - (ul - vu2 - vu3)