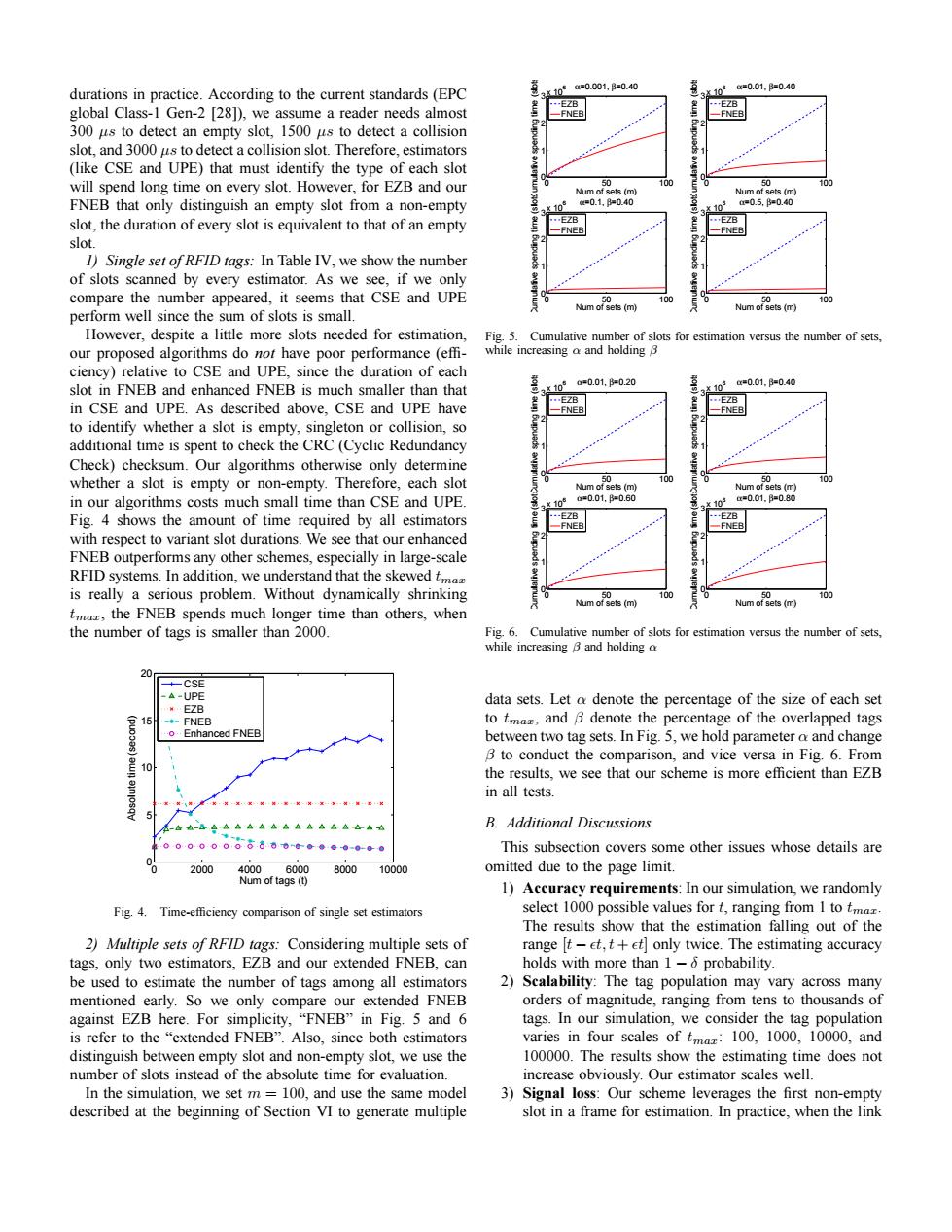
a=0.001,B=0.40 c=0.01,B=0.40 durations in practice.According to the current standards(EPC 310 EZB -EZB global Class-1 Gen-2 [28]),we assume a reader needs almost -FNEB 一FNEB 300 us to detect an empty slot,1500 us to detect a collision slot.and 3000 us to detect a collision slot.Therefore.estimators (like CSE and UPE)that must identify the type of each slot will spend long time on every slot.However,for EZB and our 50 00 00 Num of sets (m) Num of sets (m) FNEB that only distinguish an empty slot from a non-empty a=0.1,=040 10° a=0.5,=0.40 slot,the duration of every slot is equivalent to that of an empty EZB EZB -FNEB -FNEB slot. 1)Single set of RFID tags:In Table IV,we show the number of slots scanned by every estimator.As we see,if we only compare the number appeared,it seems that CSE and UPE Num(m) 100 mofes 100 perform well since the sum of slots is small. However,despite a little more slots needed for estimation, Fig.5. Cumulative number of slots for estimation versus the number of sets, our proposed algorithms do not have poor performance (effi- while increasing a and holding 3 ciency)relative to CSE and UPE,since the duration of each slot in FNEB and enhanced FNEB is much smaller than that a=0.01,=0.20 c=0.01,B=0.40 EZB EZB in CSE and UPE.As described above,CSE and UPE have FNEB FNEE to identify whether a slot is empty,singleton or collision,so additional time is spent to check the CRC(Cyclic Redundancy Check)checksum.Our algorithms otherwise only determine whether a slot is empty or non-empty.Therefore,each slot 50 100 50 00 Num of sets(m) Num of sets(m in our algorithms costs much small time than CSE and UPE. X10 a=0.01,B=0.60 X109 c=0.01,B=0.80 Fig.4 shows the amount of time required by all estimators -E7R --E78 FNEB with respect to variant slot durations.We see that our enhanced FNEB outperforms any other schemes,especially in large-scale RFID systems.In addition,we understand that the skewed tmaz is really a serious problem.Without dynamically shrinking Num of sets (m) 00 Num of ets (m) 100 tmaz,the FNEB spends much longer time than others,when the number of tags is smaller than 2000. Fig.6.Cumulative number of slots for estimation versus the number of sets, while increasing B and holding a CSE A-UPE data sets.Let a denote the percentage of the size of each set ￥EZB 615 FNEB to tmaz,and B denote the percentage of the overlapped tags oEnnanced FNEB between two tag sets.In Fig.5,we hold parameter a and change B to conduct the comparison,and vice versa in Fig.6.From 10 the results,we see that our scheme is more efficient than EZB in all tests. -△A-d合-A4A0-合4-46-合A心A4 B.Additional Discussions 00000006680-0●◆。。-00。 This subsection covers some other issues whose details are 2000 4000.6000 800010000 omitted due to the page limit. Num of tags(t) 1)Accuracy requirements:In our simulation,we randomly Fig.4.Time-efficiency comparison of single set estimators select 1000 possible values for t,ranging from I to tmar. The results show that the estimation falling out of the 2)Multiple sets of RFID tags:Considering multiple sets of range t-et,t+et only twice.The estimating accuracy tags,only two estimators,EZB and our extended FNEB,can holds with more than 1-o probability. be used to estimate the number of tags among all estimators 2) Scalability:The tag population may vary across many mentioned early.So we only compare our extended FNEB orders of magnitude,ranging from tens to thousands of against EZB here.For simplicity,"FNEB"in Fig.5 and 6 tags.In our simulation,we consider the tag population is refer to the "extended FNEB".Also,since both estimators varies in four scales of tmaz:100,1000,10000,and distinguish between empty slot and non-empty slot,we use the 100000.The results show the estimating time does not number of slots instead of the absolute time for evaluation. increase obviously.Our estimator scales well. In the simulation.we set m =100.and use the same model 3)Signal loss:Our scheme leverages the first non-empty described at the beginning of Section VI to generate multiple slot in a frame for estimation.In practice,when the linkdurations in practice. According to the current standards (EPC global Class-1 Gen-2 [28]), we assume a reader needs almost 300 µs to detect an empty slot, 1500 µs to detect a collision slot, and 3000 µs to detect a collision slot. Therefore, estimators (like CSE and UPE) that must identify the type of each slot will spend long time on every slot. However, for EZB and our FNEB that only distinguish an empty slot from a non-empty slot, the duration of every slot is equivalent to that of an empty slot. 1) Single set of RFID tags: In Table IV, we show the number of slots scanned by every estimator. As we see, if we only compare the number appeared, it seems that CSE and UPE perform well since the sum of slots is small. However, despite a little more slots needed for estimation, our proposed algorithms do not have poor performance (effi- ciency) relative to CSE and UPE, since the duration of each slot in FNEB and enhanced FNEB is much smaller than that in CSE and UPE. As described above, CSE and UPE have to identify whether a slot is empty, singleton or collision, so additional time is spent to check the CRC (Cyclic Redundancy Check) checksum. Our algorithms otherwise only determine whether a slot is empty or non-empty. Therefore, each slot in our algorithms costs much small time than CSE and UPE. Fig. 4 shows the amount of time required by all estimators with respect to variant slot durations. We see that our enhanced FNEB outperforms any other schemes, especially in large-scale RFID systems. In addition, we understand that the skewed tmax is really a serious problem. Without dynamically shrinking tmax, the FNEB spends much longer time than others, when the number of tags is smaller than 2000. 0 2000 4000 6000 8000 10000 0 5 10 15 20 Num of tags (t) Absolute time (second) CSE UPE EZB FNEB Enhanced FNEB Fig. 4. Time-efficiency comparison of single set estimators 2) Multiple sets of RFID tags: Considering multiple sets of tags, only two estimators, EZB and our extended FNEB, can be used to estimate the number of tags among all estimators mentioned early. So we only compare our extended FNEB against EZB here. For simplicity, “FNEB” in Fig. 5 and 6 is refer to the “extended FNEB”. Also, since both estimators distinguish between empty slot and non-empty slot, we use the number of slots instead of the absolute time for evaluation. In the simulation, we set m = 100, and use the same model described at the beginning of Section VI to generate multiple 0 50 100 0 1 2 3 x 106 Num of sets (m) Cumulative spending time (slots) α=0.001, β=0.40 EZB FNEB 0 50 100 0 1 2 3 x 106 Num of sets (m) Cumulative spending time (slots) α=0.01, β=0.40 EZB FNEB 0 50 100 0 1 2 3 x 106 Num of sets (m) Cumulative spending time (slots) α=0.1, β=0.40 EZB FNEB 0 50 100 0 1 2 3 x 106 Num of sets (m) Cumulative spending time (slots) α=0.5, β=0.40 EZB FNEB Fig. 5. Cumulative number of slots for estimation versus the number of sets, while increasing α and holding β 0 50 100 0 1 2 3 x 106 Num of sets (m) Cumulative spending time (slots) α=0.01, β=0.20 EZB FNEB 0 50 100 0 1 2 3 x 106 Num of sets (m) Cumulative spending time (slots) α=0.01, β=0.40 EZB FNEB 0 50 100 0 1 2 3 x 106 Num of sets (m) Cumulative spending time (slots) α=0.01, β=0.60 EZB FNEB 0 50 100 0 1 2 3 x 106 Num of sets (m) Cumulative spending time (slots) α=0.01, β=0.80 EZB FNEB Fig. 6. Cumulative number of slots for estimation versus the number of sets, while increasing β and holding α data sets. Let α denote the percentage of the size of each set to tmax, and β denote the percentage of the overlapped tags between two tag sets. In Fig. 5, we hold parameter α and change β to conduct the comparison, and vice versa in Fig. 6. From the results, we see that our scheme is more efficient than EZB in all tests. B. Additional Discussions This subsection covers some other issues whose details are omitted due to the page limit. 1) Accuracy requirements: In our simulation, we randomly select 1000 possible values for t, ranging from 1 to tmax. The results show that the estimation falling out of the range [t − ǫt, t + ǫt] only twice. The estimating accuracy holds with more than 1 − δ probability. 2) Scalability: The tag population may vary across many orders of magnitude, ranging from tens to thousands of tags. In our simulation, we consider the tag population varies in four scales of tmax: 100, 1000, 10000, and 100000. The results show the estimating time does not increase obviously. Our estimator scales well. 3) Signal loss: Our scheme leverages the first non-empty slot in a frame for estimation. In practice, when the link