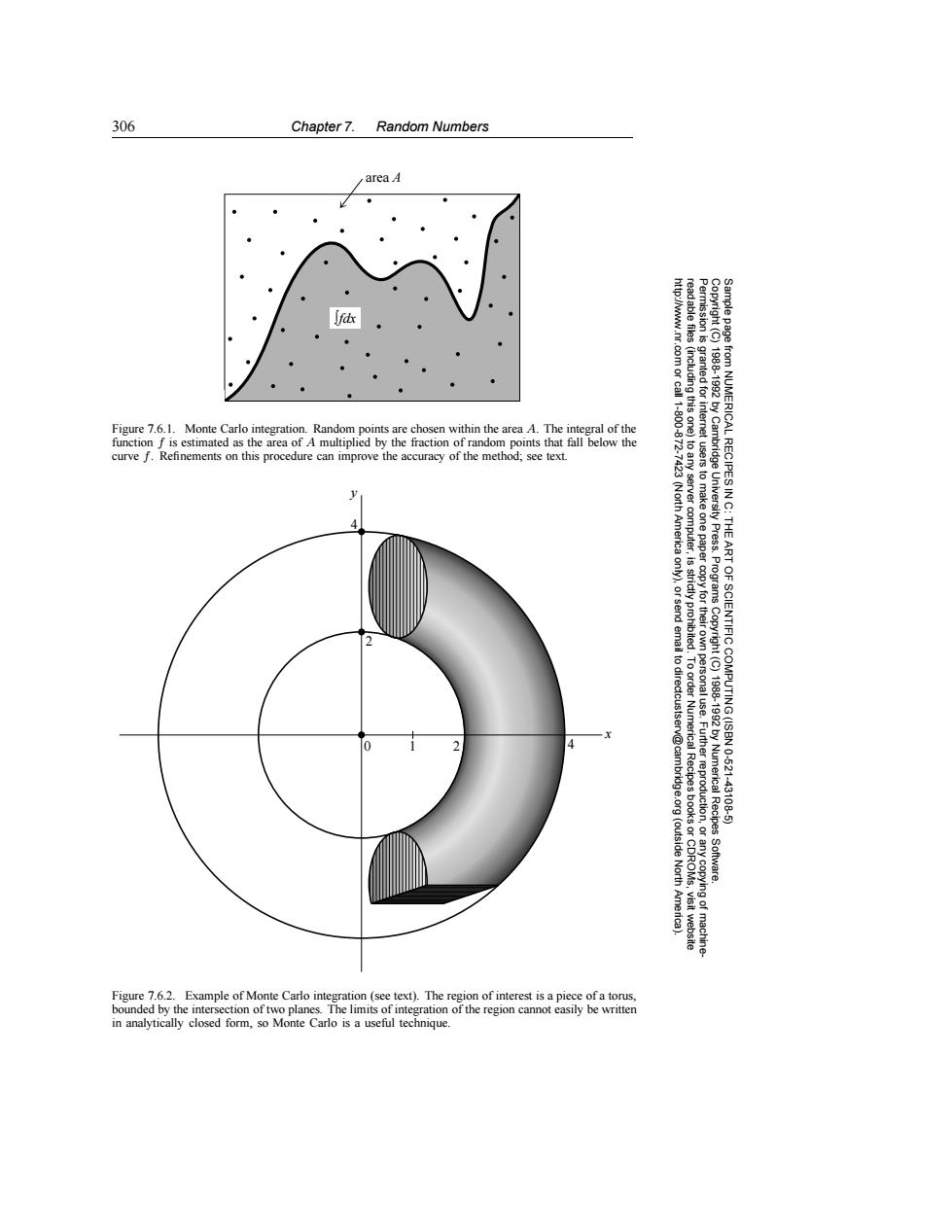
306 Chapter 7. Random Numbers area A http://www.nr.com or call 1-800 readable files (including this one) Figure 7.6.1.Monte Carlo integration.Random points are chosen within the area A.The integral of the function f is estimated as the area of A multiplied by the fraction of random points that fall below the 1872 curve f. Refinements on this procedure can improve the accuracy of the method;see text. 7423(North America Permission is granted for internet users to make one paper copy for their only),orsend email to directcustserv@cambridge.org(outside North America). Copyright (C)1988-1992 by Cambridge University Press.Programs Copyright(C)1988-1992 by Numerical Recipes Sample page from NUMERICAL RECIPES IN C:THE ART OF SCIENTIFIC COMPUTING(ISBN 0-521-43108-5) 4 Software. Figure 7.6.2.Example of Monte Carlo integration (see text).The region of interest is a piece of a torus, bounded by the intersection of two planes.The limits of integration of the region cannot easily be written in analytically closed form,so Monte Carlo is a useful technique.306 Chapter 7. Random Numbers Permission is granted for internet users to make one paper copy for their own personal use. Further reproduction, or any copyin Copyright (C) 1988-1992 by Cambridge University Press. Programs Copyright (C) 1988-1992 by Numerical Recipes Software. Sample page from NUMERICAL RECIPES IN C: THE ART OF SCIENTIFIC COMPUTING (ISBN 0-521-43108-5) g of machine￾readable files (including this one) to any server computer, is strictly prohibited. To order Numerical Recipes books or CDROMs, visit website http://www.nr.com or call 1-800-872-7423 (North America only), or send email to directcustserv@cambridge.org (outside North America). area A ∫fdx Figure 7.6.1. Monte Carlo integration. Random points are chosen within the area A. The integral of the function f is estimated as the area of A multiplied by the fraction of random points that fall below the curve f. Refinements on this procedure can improve the accuracy of the method; see text. 0 2 4 2 4 y x 1 Figure 7.6.2. Example of Monte Carlo integration (see text). The region of interest is a piece of a torus, bounded by the intersection of two planes. The limits of integration of the region cannot easily be written in analytically closed form, so Monte Carlo is a useful technique