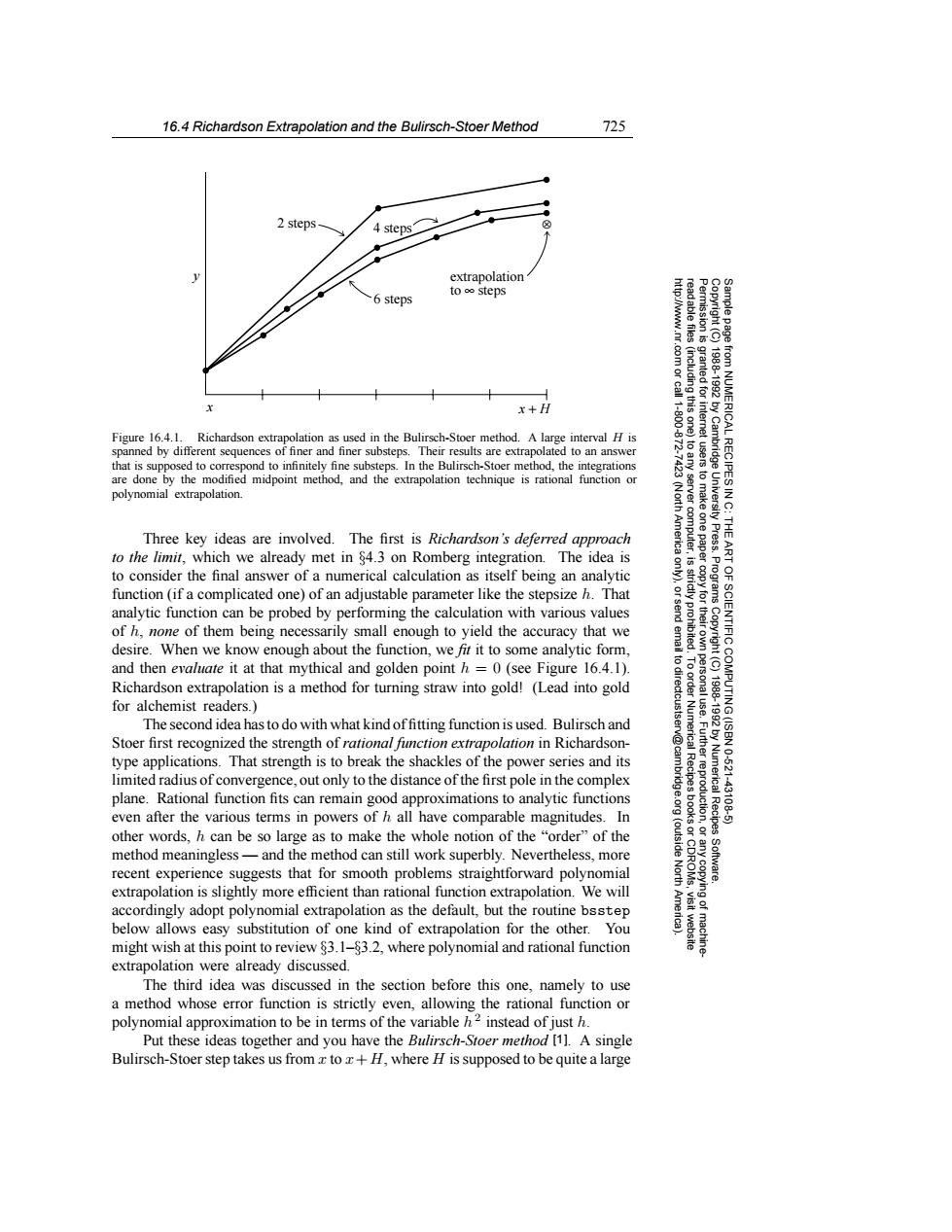
16.4 Richardson Extrapolation and the Bulirsch-Stoer Method 725 2 steps. 4 steps extrapolation to oo steps 6 steps http://www.nr read able files 83g granted for 19881992 x+H 1100 Figure 16.4.1.Richardson extrapolation as used in the Bulirsch-Stoer method.A large interval H is spanned by different sequences of finer and finer substeps.Their results are extrapolated to an answer that is supposed to correspond to infinitely fine substeps.In the Bulirsch-Stoer method,the integrations are done by the modified midpoint method,and the extrapolation technique is rational function or polynomial extrapolation. a后0 (Nort server Three key ideas are involved.The first is Richardson's deferred approach Americ computer, to the limit,which we already met in 84.3 on Romberg integration.The idea is to consider the final answer of a numerical calculation as itself being an analytic function(if a complicated one)of an adjustable parameter like the stepsize h.That analytic function can be probed by performing the calculation with various values of h,none of them being necessarily small enough to yield the accuracy that we desire.When we know enough about the function,we fit it to some analytic form, and then evaluate it at that mythical and golden point h=0(see Figure 16.4.1). 可 Richardson extrapolation is a method for turning straw into gold!(Lead into gold for alchemist readers. OF SCIENTIFIC COMPUTING (ISBN The second idea has to do with what kind offitting function is used.Bulirsch and Stoer first recognized the strength of rational function extrapolation in Richardson- type applications.That strength is to break the shackles of the power series and its Numerical Recipes 10-6211 limited radius of convergence,out only to the distance of the first pole in the complex plane.Rational function fits can remain good approximations to analytic functions uction, 43106 even after the various terms in powers of h all have comparable magnitudes.In other words.h can be so large as to make the whole notion of the "order"of the (outside method meaningless-and the method can still work superbly.Nevertheless,more recent experience suggests that for smooth problems straightforward polynomial North Software. extrapolation is slightly more efficient than rational function extrapolation.We will accordingly adopt polynomial extrapolation as the default,but the routine bsstep below allows easy substitution of one kind of extrapolation for the other.You might wish at this point to review 83.1-83.2,where polynomial and rational function extrapolation were already discussed. The third idea was discussed in the section before this one,namely to use a method whose error function is strictly even,allowing the rational function or polynomial approximation to be in terms of the variable h2 instead of just h. Put these ideas together and you have the Bulirsch-Stoer method [11.A single Bulirsch-Stoer step takes us from x to +H,where H is supposed to be quite a large16.4 Richardson Extrapolation and the Bulirsch-Stoer Method 725 Permission is granted for internet users to make one paper copy for their own personal use. Further reproduction, or any copyin Copyright (C) 1988-1992 by Cambridge University Press. Programs Copyright (C) 1988-1992 by Numerical Recipes Software. Sample page from NUMERICAL RECIPES IN C: THE ART OF SCIENTIFIC COMPUTING (ISBN 0-521-43108-5) g of machine￾readable files (including this one) to any server computer, is strictly prohibited. To order Numerical Recipes books or CDROMs, visit website http://www.nr.com or call 1-800-872-7423 (North America only), or send email to directcustserv@cambridge.org (outside North America). 6 steps 2 steps 4 steps ⊗ extrapolation to ∞ steps x x + H y Figure 16.4.1. Richardson extrapolation as used in the Bulirsch-Stoer method. A large interval H is spanned by different sequences of finer and finer substeps. Their results are extrapolated to an answer that is supposed to correspond to infinitely fine substeps. In the Bulirsch-Stoer method, the integrations are done by the modified midpoint method, and the extrapolation technique is rational function or polynomial extrapolation. Three key ideas are involved. The first is Richardson’s deferred approach to the limit, which we already met in §4.3 on Romberg integration. The idea is to consider the final answer of a numerical calculation as itself being an analytic function (if a complicated one) of an adjustable parameter like the stepsize h. That analytic function can be probed by performing the calculation with various values of h, none of them being necessarily small enough to yield the accuracy that we desire. When we know enough about the function, we fit it to some analytic form, and then evaluate it at that mythical and golden point h = 0 (see Figure 16.4.1). Richardson extrapolation is a method for turning straw into gold! (Lead into gold for alchemist readers.) The second idea has to do with what kind of fitting function is used. Bulirsch and Stoer first recognized the strength of rational function extrapolation in Richardson￾type applications. That strength is to break the shackles of the power series and its limited radius of convergence, out only to the distance of the first pole in the complex plane. Rational function fits can remain good approximations to analytic functions even after the various terms in powers of h all have comparable magnitudes. In other words, h can be so large as to make the whole notion of the “order” of the method meaningless — and the method can still work superbly. Nevertheless, more recent experience suggests that for smooth problems straightforward polynomial extrapolation is slightly more efficient than rational function extrapolation. We will accordingly adopt polynomial extrapolation as the default, but the routine bsstep below allows easy substitution of one kind of extrapolation for the other. You might wish at this point to review §3.1–§3.2, where polynomial and rational function extrapolation were already discussed. The third idea was discussed in the section before this one, namely to use a method whose error function is strictly even, allowing the rational function or polynomial approximation to be in terms of the variable h2 instead of just h. Put these ideas together and you have the Bulirsch-Stoer method [1]. A single Bulirsch-Stoer step takes us from x to x+H, where H is supposed to be quite a large