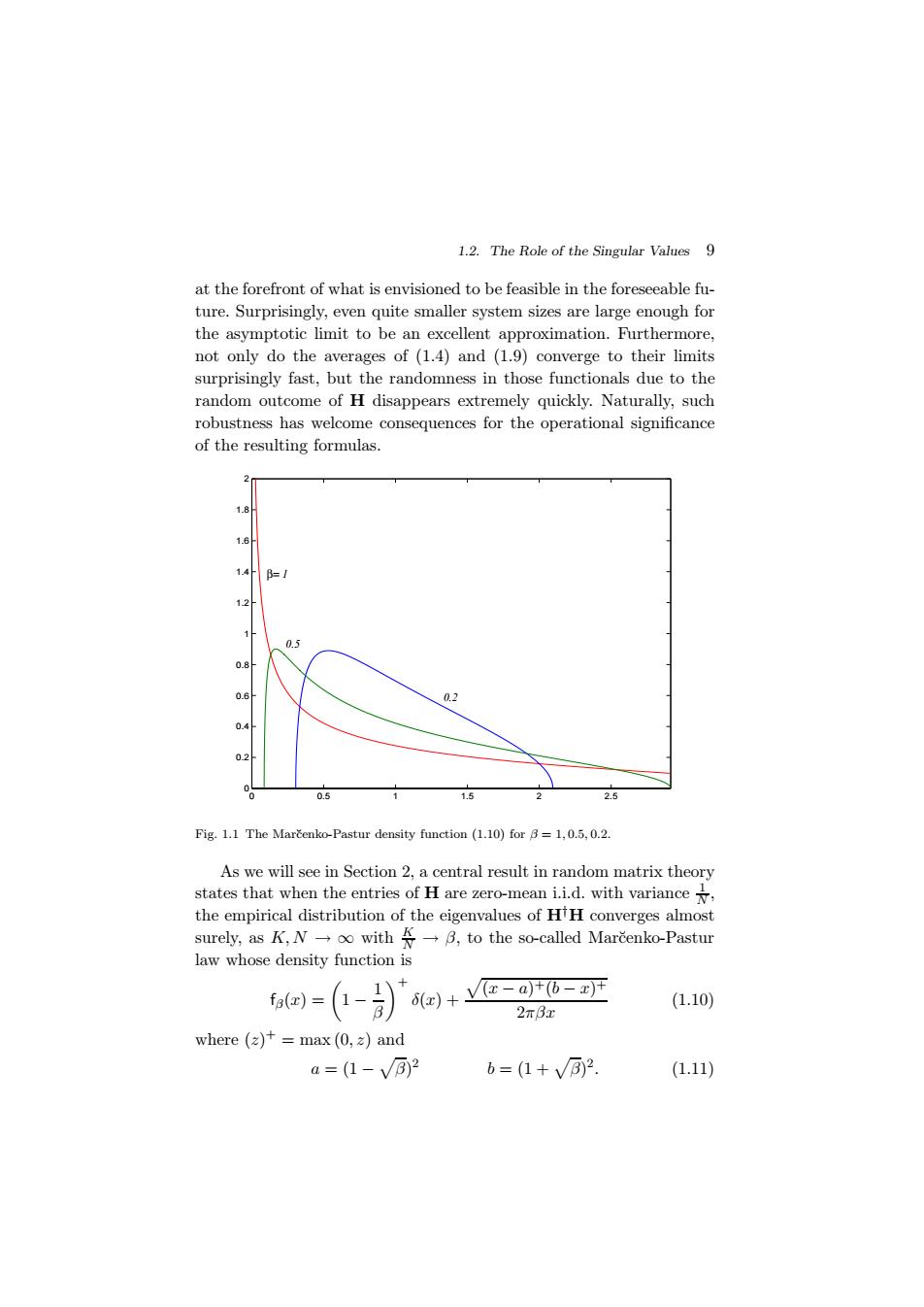
1.2.The Role of the Singular Values 9 at the forefront of what is envisioned to be feasible in the foreseeable fu- ture.Surprisingly,even quite smaller system sizes are large enough for the asymptotic limit to be an excellent approximation.Furthermore, not only do the averages of (1.4)and (1.9)converge to their limits surprisingly fast,but the randomness in those functionals due to the random outcome of H disappears extremely quickly.Naturally,such robustness has welcome consequences for the operational significance of the resulting formulas. 1.8 14 B=1 0.5 0 0.2 0.5 1.5 2.5 Fig.1.1 The Marcenko-Pastur density function (1.10)for B=1,0.5,0.2. As we will see in Section 2,a central result in random matrix theory states that when the entries of H are zero-mean i.i.d.with variance y, the empirical distribution of the eigenvalues of HH converges almost surely,asK,V一oo with→3，to the so-called Mar心enko-Pastur law whose density function is =(-动) x)+-Ot6-开 (1.10) 2π3x where (z)+=max(0,z)and a=(1-VE2 b=(1+V2. (1.11)1.2. The Role of the Singular Values 9 at the forefront of what is envisioned to be feasible in the foreseeable fu￾ture. Surprisingly, even quite smaller system sizes are large enough for the asymptotic limit to be an excellent approximation. Furthermore, not only do the averages of (1.4) and (1.9) converge to their limits surprisingly fast, but the randomness in those functionals due to the random outcome of H disappears extremely quickly. Naturally, such robustness has welcome consequences for the operational significance of the resulting formulas. 0 0.5 1 1.5 2 2.5 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 β= 0.2 0.5 1 Fig. 1.1 The Mar˘cenko-Pastur density function (1.10) for β = 1, 0.5, 0.2. As we will see in Section 2, a central result in random matrix theory states that when the entries of H are zero-mean i.i.d. with variance 1 N , the empirical distribution of the eigenvalues of H†H converges almost surely, as K, N → ∞ with K N → β, to the so-called Mar˘cenko-Pastur law whose density function is fβ(x) = 1 − 1 β + δ(x) + (x − a)+(b − x)+ 2πβx (1.10) where (z)+ = max (0, z) and a = (1 − β) 2 b = (1 + β) 2. (1.11)