正在加载图片...
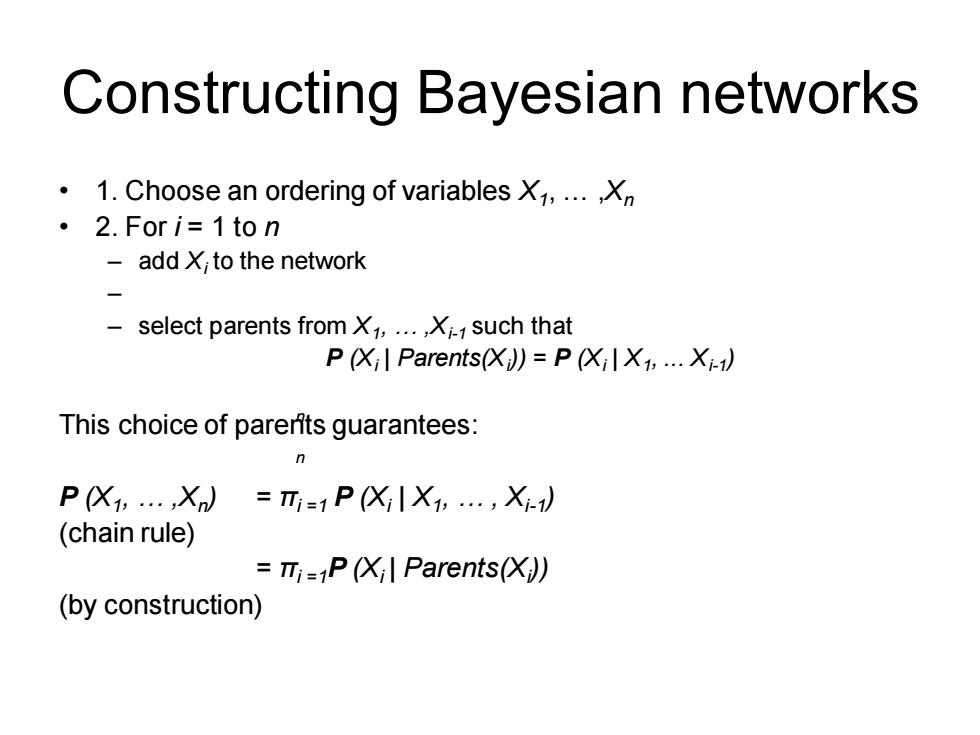
Constructing Bayesian networks 1.Choose an ordering of variables X1,...,Xn 2.For i=1 to n add X;to the network select parents from X1,...,X such that P(Xil Parents(X))=P(XilX1,...Xi-1) This choice of parerits guarantees: P (X1....Xn)=Ti=1P(XilX1:....Xi-1) (chain rule) =mi=P(Xil Parents(X》 (by construction) Constructing Bayesian networks • 1. Choose an ordering of variables X1 , … ,Xn • 2. For i = 1 to n – add Xi to the network – – select parents from X1 , … ,Xi-1 such that P (Xi | Parents(Xi )) = P (Xi | X1 , ... Xi-1 ) This choice of parents guarantees: P (X1 , … ,Xn ) = πi =1 P (Xi | X1 , … , Xi-1 ) (chain rule) = πi =1P (Xi | Parents(Xi )) (by construction) n n