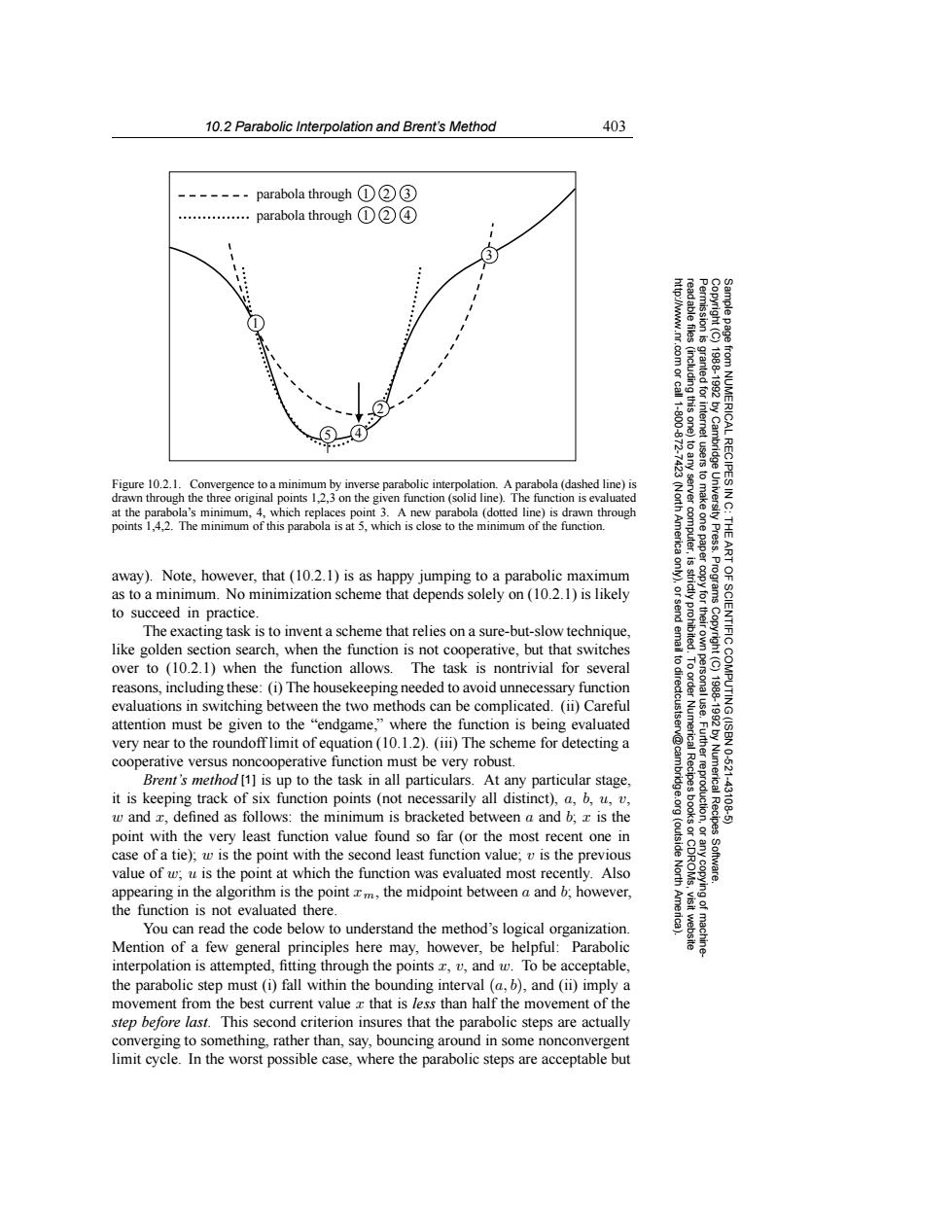
10.2 Parabolic Interpolation and Brent's Method 403 ------parabola through①②③ 。。。。。:。。。。。et parabola through①②④ .com or call (including this one) 19881992 5 111800-672 Figure 10.2.1.Convergence to aminimum by inverse parabolic interpolation.A parabola(dashed line)is server from NUMERICAL RECIPES IN C: drawn through the three original points 1,2,3 on the given function (solid line).The function is evaluated (Nort at the parabola's minimum,4,which replaces point 3.A new parabola (dotted line)is drawn through points 1,4,2.The minimum of this parabola is at 5,which is close to the minimum of the function. America computer, away).Note,however,that(10.2.1)is as happy jumping to a parabolic maximum as to a minimum.No minimization scheme that depends solely on(10.2.1)is likely to succeed in practice. The exacting task is to invent a scheme that relies on a sure-but-slow technique, OF SCIENTIFIC like golden section search,when the function is not cooperative,but that switches over to (10.2.1)when the function allows.The task is nontrivial for several reasons,including these:(i)The housekeeping needed to avoid unnecessary function evaluations in switching between the two methods can be complicated.(ii)Careful attention must be given to the "endgame,"where the function is being evaluated very near to the roundofflimit of equation(10.1.2).(iii)The scheme for detecting a cooperative versus noncooperative function must be very robust. Brent's method [1]is up to the task in all particulars.At any particular stage, it is keeping track of six function points (not necessarily all distinct),a,b,u,v, Fuurggoglrion Numerical Recipes 10-521 4310 w and z.defined as follows:the minimum is bracketed between a and b:z is the point with the very least function value found so far(or the most recent one in (outside g case of a tie);w is the point with the second least function value;v is the previous value of w:u is the point at which the function was evaluated most recently.Also North Software. appearing in the algorithm is the point xm,the midpoint between a and b;however, the function is not evaluated there. You can read the code below to understand the method's logical organization. Mention of a few general principles here may,however,be helpful:Parabolic interpolation is attempted,fitting through the points v,and w.To be acceptable, the parabolic step must (i)fall within the bounding interval (a,b),and(ii)imply a movement from the best current value that is less than half the movement of the step before last.This second criterion insures that the parabolic steps are actually converging to something,rather than,say,bouncing around in some nonconvergent limit cycle.In the worst possible case,where the parabolic steps are acceptable but10.2 Parabolic Interpolation and Brent’s Method 403 Permission is granted for internet users to make one paper copy for their own personal use. Further reproduction, or any copyin Copyright (C) 1988-1992 by Cambridge University Press. Programs Copyright (C) 1988-1992 by Numerical Recipes Software. Sample page from NUMERICAL RECIPES IN C: THE ART OF SCIENTIFIC COMPUTING (ISBN 0-521-43108-5) g of machine￾readable files (including this one) to any server computer, is strictly prohibited. To order Numerical Recipes books or CDROMs, visit website http://www.nr.com or call 1-800-872-7423 (North America only), or send email to directcustserv@cambridge.org (outside North America). 1 4 2 3 parabola through 1 2 3 parabola through 1 2 4 5 Figure 10.2.1. Convergence to a minimum by inverse parabolic interpolation. A parabola (dashed line) is drawn through the three original points 1,2,3 on the given function (solid line). The function is evaluated at the parabola’s minimum, 4, which replaces point 3. A new parabola (dotted line) is drawn through points 1,4,2. The minimum of this parabola is at 5, which is close to the minimum of the function. away). Note, however, that (10.2.1) is as happy jumping to a parabolic maximum as to a minimum. No minimization scheme that depends solely on (10.2.1) is likely to succeed in practice. The exacting task is to invent a scheme that relies on a sure-but-slow technique, like golden section search, when the function is not cooperative, but that switches over to (10.2.1) when the function allows. The task is nontrivial for several reasons, including these: (i) The housekeeping needed to avoid unnecessary function evaluations in switching between the two methods can be complicated. (ii) Careful attention must be given to the “endgame,” where the function is being evaluated very near to the roundoff limit of equation (10.1.2). (iii) The scheme for detecting a cooperative versus noncooperative function must be very robust. Brent’s method [1] is up to the task in all particulars. At any particular stage, it is keeping track of six function points (not necessarily all distinct), a, b, u, v, w and x, defined as follows: the minimum is bracketed between a and b; x is the point with the very least function value found so far (or the most recent one in case of a tie); w is the point with the second least function value; v is the previous value of w; u is the point at which the function was evaluated most recently. Also appearing in the algorithm is the point xm, the midpoint between a and b; however, the function is not evaluated there. You can read the code below to understand the method’s logical organization. Mention of a few general principles here may, however, be helpful: Parabolic interpolation is attempted, fitting through the points x, v, and w. To be acceptable, the parabolic step must (i) fall within the bounding interval (a, b), and (ii) imply a movement from the best current value x that is less than half the movement of the step before last. This second criterion insures that the parabolic steps are actually converging to something, rather than, say, bouncing around in some nonconvergent limit cycle. In the worst possible case, where the parabolic steps are acceptable but