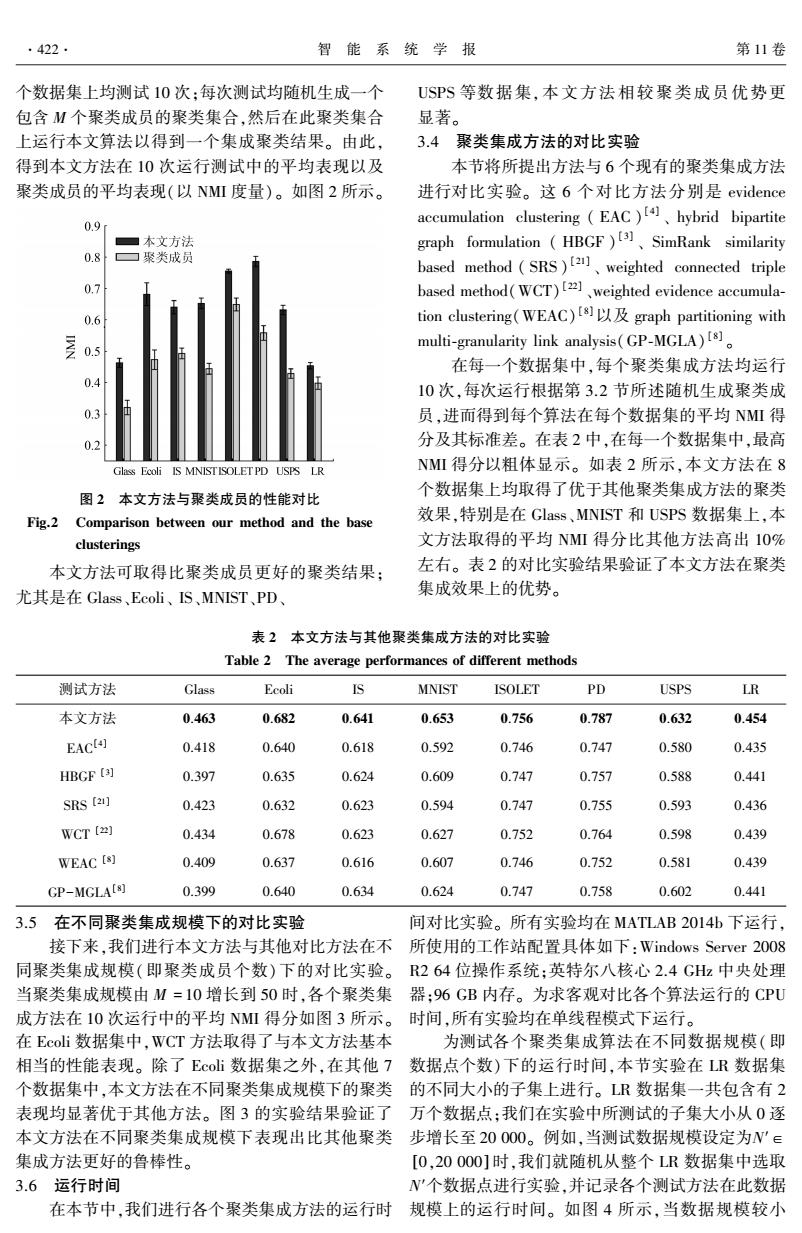
.422 智能系统学报 第11卷 个数据集上均测试10次：每次测试均随机生成一个 USPS等数据集，本文方法相较聚类成员优势更 包含M个聚类成员的聚类集合，然后在此聚类集合 显著。 上运行本文算法以得到一个集成聚类结果。由此， 3.4聚类集成方法的对比实验 得到本文方法在10次运行测试中的平均表现以及 本节将所提出方法与6个现有的聚类集成方法 聚类成员的平均表现（以NMI度量）。如图2所示。 进行对比实验。这6个对比方法分别是evidence accumulation clustering (EAC)hybrid bipartite 0.9 本文方法 graph formulation (HBGF)SimRank similarity 0.8 口聚类成员 based method (SRS)weighted connected triple 0.7 based method(WCT)[2],weighted evidence accumula- 0.6 tion clustering(WEAC)sgraph partitioning with multi-granularity link analysis(GP-MGLA)[8] 0.5 在每一个数据集中，每个聚类集成方法均运行 0.4 10次，每次运行根据第3.2节所述随机生成聚类成 0.3 员，进而得到每个算法在每个数据集的平均NMI得 0.2 分及其标准差。在表2中，在每一个数据集中，最高 Glass Ecoli IS MNISTISOLETPD USPS LR NM得分以粗体显示。如表2所示，本文方法在8 个数据集上均取得了优于其他聚类集成方法的聚类 图2本文方法与聚类成员的性能对比 Fig.2 Comparison between our method and the base 效果，特别是在Glass、MNIST和USPS数据集上，本 clusterings 文方法取得的平均NMI得分比其他方法高出10% 本文方法可取得比聚类成员更好的聚类结果： 左右。表2的对比实验结果验证了本文方法在聚类 尤其是在Glass、Ecoli、IS、MNIST、PD、 集成效果上的优势。 表2本文方法与其他聚类集成方法的对比实验 Table 2 The average performances of different methods 测试方法 Glass Ecoli IS MNIST ISOLET PD USPS LR 本文方法 0.463 0.682 0.641 0.653 0.756 0.787 0.632 0.454 EACt4] 0.418 0.640 0.618 0.592 0.746 0.747 0.580 0.435 HBGF ( 0.397 0.635 0.624 0.609 0.747 0.757 0.588 0.441 SRS [21] 0.423 0.632 0.623 0.594 0.747 0.755 0.593 0.436 WCT [z) 0.434 0.678 0.623 0.627 0.752 0.764 0.598 0.439 WEAC [s] 0.409 0.637 0.616 0.607 0.746 0.752 0.581 0.439 GP-MGLA[8) 0.399 0.640 0.634 0.624 0.747 0.758 0.602 0.441 3.5在不同聚类集成规模下的对比实验 间对比实验。所有实验均在MATLAB2014h下运行， 接下来，我们进行本文方法与其他对比方法在不所使用的工作站配置具体如下：Windows Server2008 同聚类集成规模（即聚类成员个数）下的对比实验。R264位操作系统：英特尔八核心2.4GHz中央处理 当聚类集成规模由M=10增长到50时，各个聚类集器：96GB内存。为求客观对比各个算法运行的CPU 成方法在10次运行中的平均NM得分如图3所示。时间，所有实验均在单线程模式下运行。 在Ecoli数据集中，WCT方法取得了与本文方法基本 为测试各个聚类集成算法在不同数据规模（即 相当的性能表现。除了Ecoi数据集之外，在其他7数据点个数)下的运行时间，本节实验在LR数据集 个数据集中，本文方法在不同聚类集成规模下的聚类的不同大小的子集上进行。LR数据集一共包含有2 表现均显著优于其他方法。图3的实验结果验证了万个数据点：我们在实验中所测试的子集大小从0逐 本文方法在不同聚类集成规模下表现出比其他聚类步增长至20000。例如，当测试数据规模设定为W'∈ 集成方法更好的鲁棒性。 [0,20000]时，我们就随机从整个LR数据集中选取 3.6运行时间 N'个数据点进行实验，并记录各个测试方法在此数据 在本节中，我们进行各个聚类集成方法的运行时规模上的运行时间。如图4所示，当数据规模较小个数据集上均测试 １０ 次；每次测试均随机生成一个 包含 Ｍ 个聚类成员的聚类集合，然后在此聚类集合 上运行本文算法以得到一个集成聚类结果。 由此， 得到本文方法在 １０ 次运行测试中的平均表现以及 聚类成员的平均表现（以 ＮＭＩ 度量）。 如图 ２ 所示。 图 ２ 本文方法与聚类成员的性能对比 Ｆｉｇ．２ Ｃｏｍｐａｒｉｓｏｎ ｂｅｔｗｅｅｎ ｏｕｒ ｍｅｔｈｏｄ ａｎｄ ｔｈｅ ｂａｓｅ ｃｌｕｓｔｅｒｉｎｇｓ 本文方法可取得比聚类成员更好的聚类结果； 尤其是在 Ｇｌａｓｓ、Ｅｃｏｌｉ、 ＩＳ、ＭＮＩＳＴ、ＰＤ、 ＵＳＰＳ 等数据集，本文方法相较聚类成员优势更 显著。 ３．４ 聚类集成方法的对比实验 本节将所提出方法与 ６ 个现有的聚类集成方法 进行对比实验。 这 ６ 个对比方法分别是 ｅｖｉｄｅｎｃｅ ａｃｃｕｍｕｌａｔｉｏｎ ｃｌｕｓｔｅｒｉｎｇ （ ＥＡＣ ） ［４］ 、 ｈｙｂｒｉｄ ｂｉｐａｒｔｉｔｅ ｇｒａｐｈ ｆｏｒｍｕｌａｔｉｏｎ （ ＨＢＧＦ ） ［３］ 、 ＳｉｍＲａｎｋ ｓｉｍｉｌａｒｉｔｙ ｂａｓｅｄ ｍｅｔｈｏｄ （ ＳＲＳ ） ［２１］ 、 ｗｅｉｇｈｔｅｄ ｃｏｎｎｅｃｔｅｄ ｔｒｉｐｌｅ ｂａｓｅｄ ｍｅｔｈｏｄ（ＷＣＴ） ［２２］ 、ｗｅｉｇｈｔｅｄ ｅｖｉｄｅｎｃｅ ａｃｃｕｍｕｌａ⁃ ｔｉｏｎ ｃｌｕｓｔｅｒｉｎｇ（ＷＥＡＣ） ［８］以及 ｇｒａｐｈ ｐａｒｔｉｔｉｏｎｉｎｇ ｗｉｔｈ ｍｕｌｔｉ⁃ｇｒａｎｕｌａｒｉｔｙ ｌｉｎｋ ａｎａｌｙｓｉｓ（ＧＰ⁃ＭＧＬＡ） ［８］ 。 在每一个数据集中，每个聚类集成方法均运行 １０ 次，每次运行根据第 ３．２ 节所述随机生成聚类成 员，进而得到每个算法在每个数据集的平均 ＮＭＩ 得 分及其标准差。 在表 ２ 中，在每一个数据集中，最高 ＮＭＩ 得分以粗体显示。 如表 ２ 所示，本文方法在 ８ 个数据集上均取得了优于其他聚类集成方法的聚类 效果，特别是在 Ｇｌａｓｓ、ＭＮＩＳＴ 和 ＵＳＰＳ 数据集上，本 文方法取得的平均 ＮＭＩ 得分比其他方法高出 １０％ 左右。 表 ２ 的对比实验结果验证了本文方法在聚类 集成效果上的优势。 表 ２ 本文方法与其他聚类集成方法的对比实验 Ｔａｂｌｅ ２ Ｔｈｅ ａｖｅｒａｇｅ ｐｅｒｆｏｒｍａｎｃｅｓ ｏｆ ｄｉｆｆｅｒｅｎｔ ｍｅｔｈｏｄｓ 测试方法 Ｇｌａｓｓ Ｅｃｏｌｉ ＩＳ ＭＮＩＳＴ ＩＳＯＬＥＴ ＰＤ ＵＳＰＳ ＬＲ 本文方法 ０．４６３ ０．６８２ ０．６４１ ０．６５３ ０．７５６ ０．７８７ ０．６３２ ０．４５４ ＥＡＣ ［４］ ０．４１８ ０．６４０ ０．６１８ ０．５９２ ０．７４６ ０．７４７ ０．５８０ ０．４３５ ＨＢＧＦ ［３］ ０．３９７ ０．６３５ ０．６２４ ０．６０９ ０．７４７ ０．７５７ ０．５８８ ０．４４１ ＳＲＳ ［２１］ ０．４２３ ０．６３２ ０．６２３ ０．５９４ ０．７４７ ０．７５５ ０．５９３ ０．４３６ ＷＣＴ ［２２］ ０．４３４ ０．６７８ ０．６２３ ０．６２７ ０．７５２ ０．７６４ ０．５９８ ０．４３９ ＷＥＡＣ ［８］ ０．４０９ ０．６３７ ０．６１６ ０．６０７ ０．７４６ ０．７５２ ０．５８１ ０．４３９ ＧＰ－ＭＧＬＡ ［８］ ０．３９９ ０．６４０ ０．６３４ ０．６２４ ０．７４７ ０．７５８ ０．６０２ ０．４４１ ３．５ 在不同聚类集成规模下的对比实验 接下来，我们进行本文方法与其他对比方法在不 同聚类集成规模（即聚类成员个数）下的对比实验。 当聚类集成规模由 Ｍ ＝ １０ 增长到 ５０ 时，各个聚类集 成方法在 １０ 次运行中的平均 ＮＭＩ 得分如图 ３ 所示。 在 Ｅｃｏｌｉ 数据集中，ＷＣＴ 方法取得了与本文方法基本 相当的性能表现。 除了 Ｅｃｏｌｉ 数据集之外，在其他 ７ 个数据集中，本文方法在不同聚类集成规模下的聚类 表现均显著优于其他方法。 图 ３ 的实验结果验证了 本文方法在不同聚类集成规模下表现出比其他聚类 集成方法更好的鲁棒性。 ３．６ 运行时间 在本节中，我们进行各个聚类集成方法的运行时 间对比实验。 所有实验均在 ＭＡＴＬＡＢ ２０１４ｂ 下运行， 所使用的工作站配置具体如下：Ｗｉｎｄｏｗｓ Ｓｅｒｖｅｒ ２００８ Ｒ２ ６４ 位操作系统；英特尔八核心 ２．４ ＧＨｚ 中央处理 器；９６ ＧＢ 内存。 为求客观对比各个算法运行的 ＣＰＵ 时间，所有实验均在单线程模式下运行。 为测试各个聚类集成算法在不同数据规模（即 数据点个数）下的运行时间，本节实验在 ＬＲ 数据集 的不同大小的子集上进行。 ＬＲ 数据集一共包含有 ２ 万个数据点；我们在实验中所测试的子集大小从 ０ 逐 步增长至 ２０ ０００。 例如，当测试数据规模设定为Ｎ′∈ [０，２０ ０００] 时，我们就随机从整个 ＬＲ 数据集中选取 Ｎ′个数据点进行实验，并记录各个测试方法在此数据 规模上的运行时间。 如图 ４ 所示，当数据规模较小 ·４２２· 智 能 系 统 学 报 第 １１ 卷