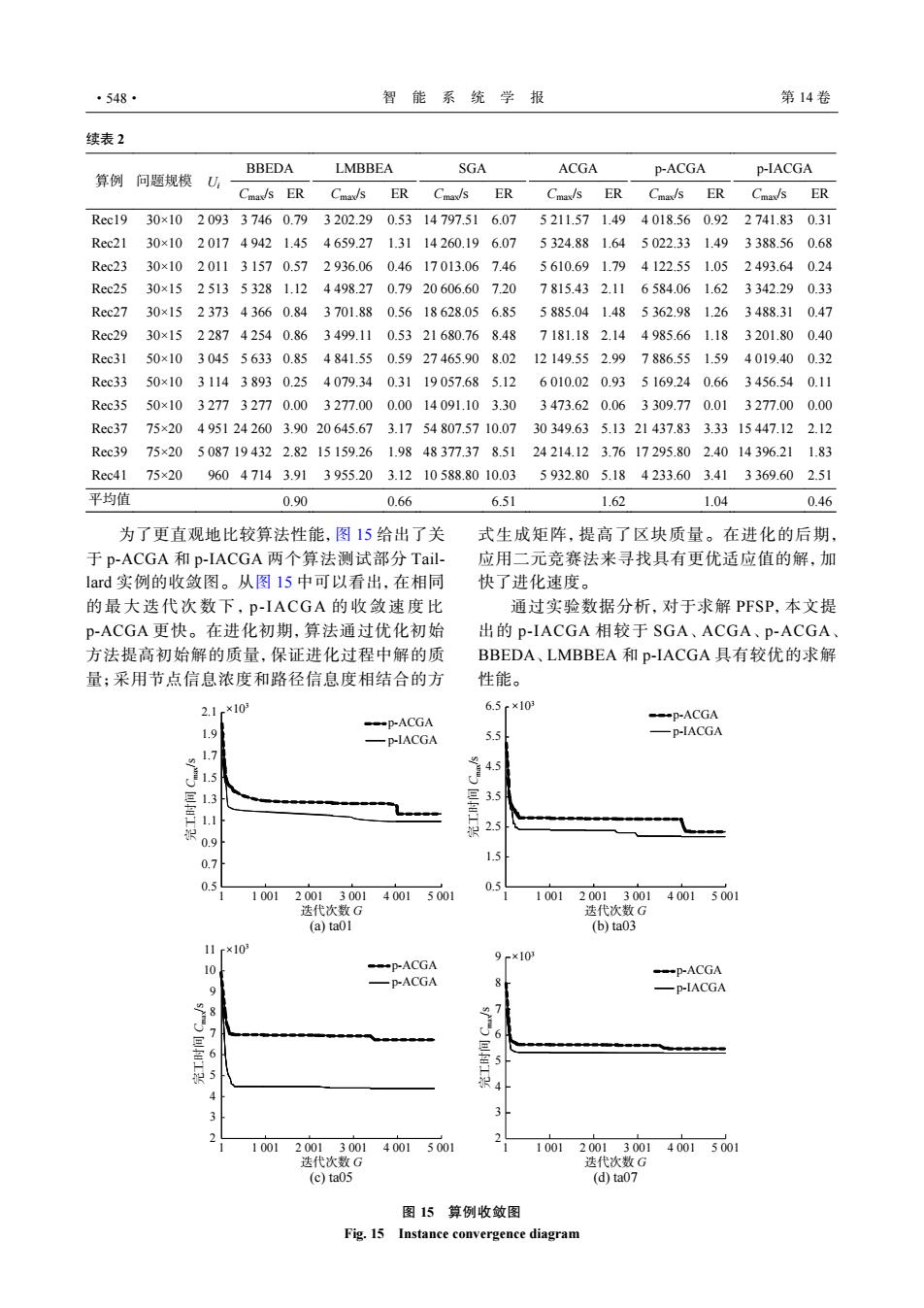
·548· 智能系统学报 第14卷 续表2 BBEDA LMBBEA SGA ACGA P-ACGA P-IACGA 算例问题规模 U Cma/s ER Cmad/s ER Cmax/s ER Cmad/s ER Cmax/s ER Cmay/s ER Rec1930×10209337460.793202.290.5314797.516.075211.571.494018.560.922741.830.31 Rec21 30×10201749421.45 4659.271.3114260.196.07 5324.881.64 5022.331.49 3388.560.68 Rec2330x10 201131570.572936.060.4617013.067.46 5610.691.79 4122.551.05 2493.640.24 Rec2530×15251353281.124498.270.7920606.607.20 7815.432.116584.061.62 3342.290.33 Rec2730×15237343660.843701.880.5618628.056.855885.041.485362.981.26 3488.310.47 Rec2930×15228742540.863499.110.5321680.768.487181.182.144985.661.18 3201.800.40 Rec3150×10304556330.854841.550.5927465.908.0212149.552.997886.551.59 4019.400.32 Rec3350×10311438930.254079.340.3119057.685.126010.020.935169.240.66 3456.540.11 Rec3550×10327732770.003277.000.0014091.103.303473.620.063309.770.01 3277.000.00 Rec3775×204951242603.9020645.673.1754807.5710.0730349.635.1321437.833.3315447.122.12 Rec39 75×205087194322.8215159.261.9848377.378.5124214.123.7617295.802.4014396.211.83 Rec4175×2096047143.913955.203.1210588.8010.03 5932.805.184233.603.413369.602.51 平均值 0.90 0.66 6.51 1.62 1.04 0.46 为了更直观地比较算法性能，图15给出了关 式生成矩阵，提高了区块质量。在进化的后期 于p-ACGA和p-IACGA两个算法测试部分Tail- 应用二元竞赛法来寻找具有更优适应值的解，加 lard实例的收敛图。从图l5中可以看出，在相同 快了进化速度。 的最大迭代次数下，p-IACGA的收敛速度比 通过实验数据分析，对于求解PFSP,本文提 p-ACGA更快。在进化初期，算法通过优化初始 出的p-IACGA相较于SGA、ACGA、P-ACGA、 方法提高初始解的质量，保证进化过程中解的质 BBEDA、LMBBEA和p-IACGA具有较优的求解 量；采用节点信息浓度和路径信息度相结合的方 性能。 2.1r×10 6.5r×10 -p-ACGA --p-ACGA 1.9 P-IACGA 5.5 一p-IACGA 4.5 3.5 2.5 0.9 07 1.5 0.5 0.5 10012001300140015001 10012001300140015001 迭代次数G 迭代次数G (a)ta0l (b)ta03 11r×10 9-×10 10 p-ACGA p-ACGA -p-ACGA 9 -D-IACGA 6 100120013001 40015001 1001.2001300140015001 迭代次数G 迭代次数G (c)ta05 (d)ta07 图15算例收敛图 Fig.15 Instance convergence diagram为了更直观地比较算法性能，图 15 给出了关 于 p-ACGA 和 p-IACGA 两个算法测试部分 Tail￾lard 实例的收敛图。从图 15 中可以看出，在相同 的最大迭代次数下， p-IACGA 的收敛速度比 p-ACGA 更快。在进化初期，算法通过优化初始 方法提高初始解的质量，保证进化过程中解的质 量；采用节点信息浓度和路径信息度相结合的方 式生成矩阵，提高了区块质量。在进化的后期， 应用二元竞赛法来寻找具有更优适应值的解，加 快了进化速度。 通过实验数据分析，对于求解 PFSP，本文提 出的 p-IACGA 相较于 SGA、ACGA、p-ACGA、 BBEDA、LMBBEA 和 p-IACGA 具有较优的求解 性能。 0.5 0.7 0.9 1.1 1.3 1.5 1.7 1.9 2.1 ×103 ×103 ×103 ×103 1 1 001 2 001 3 001 4 001 5 001 完工时间 Cmax/s 迭代次数 G (a) ta01 (c) ta05 (d) ta07 (b) ta03 p-ACGA p-IACGA 0.5 1.5 2.5 3.5 4.5 5.5 6.5 1 1 001 2 001 3 001 4 001 5 001 完工时间 Cmax/s 迭代次数 G p-ACGA p-IACGA 2 3 4 5 6 7 8 9 10 11 1 1 001 2 001 3 001 4 001 5 001 完工时间 Cmax/s 迭代次数 G p-ACGA p-ACGA 2 3 4 5 6 7 8 9 1 1 001 2 001 3 001 4 001 5 001 完工时间 Cmax/s 迭代次数 G p-ACGA p-IACGA 图 15 算例收敛图 Fig. 15 Instance convergence diagram 续表 2 算例 问题规模 Ui BBEDA LMBBEA SGA ACGA p-ACGA p-IACGA Cmax/s ER Cmax/s ER Cmax/s ER Cmax/s ER Cmax/s ER Cmax/s ER Rec19 30×10 2 093 3 746 0.79 3 202.29 0.53 14 797.51 6.07 5 211.57 1.49 4 018.56 0.92 2 741.83 0.31 Rec21 30×10 2 017 4 942 1.45 4 659.27 1.31 14 260.19 6.07 5 324.88 1.64 5 022.33 1.49 3 388.56 0.68 Rec23 30×10 2 011 3 157 0.57 2 936.06 0.46 17 013.06 7.46 5 610.69 1.79 4 122.55 1.05 2 493.64 0.24 Rec25 30×15 2 513 5 328 1.12 4 498.27 0.79 20 606.60 7.20 7 815.43 2.11 6 584.06 1.62 3 342.29 0.33 Rec27 30×15 2 373 4 366 0.84 3 701.88 0.56 18 628.05 6.85 5 885.04 1.48 5 362.98 1.26 3 488.31 0.47 Rec29 30×15 2 287 4 254 0.86 3 499.11 0.53 21 680.76 8.48 7 181.18 2.14 4 985.66 1.18 3 201.80 0.40 Rec31 50×10 3 045 5 633 0.85 4 841.55 0.59 27 465.90 8.02 12 149.55 2.99 7 886.55 1.59 4 019.40 0.32 Rec33 50×10 3 114 3 893 0.25 4 079.34 0.31 19 057.68 5.12 6 010.02 0.93 5 169.24 0.66 3 456.54 0.11 Rec35 50×10 3 277 3 277 0.00 3 277.00 0.00 14 091.10 3.30 3 473.62 0.06 3 309.77 0.01 3 277.00 0.00 Rec37 75×20 4 951 24 260 3.90 20 645.67 3.17 54 807.57 10.07 30 349.63 5.13 21 437.83 3.33 15 447.12 2.12 Rec39 75×20 5 087 19 432 2.82 15 159.26 1.98 48 377.37 8.51 24 214.12 3.76 17 295.80 2.40 14 396.21 1.83 Rec41 75×20 960 4 714 3.91 3 955.20 3.12 10 588.80 10.03 5 932.80 5.18 4 233.60 3.41 3 369.60 2.51 平均值 0.90 0.66 6.51 1.62 1.04 0.46 ·548· 智 能 系 统 学 报 第 14 卷