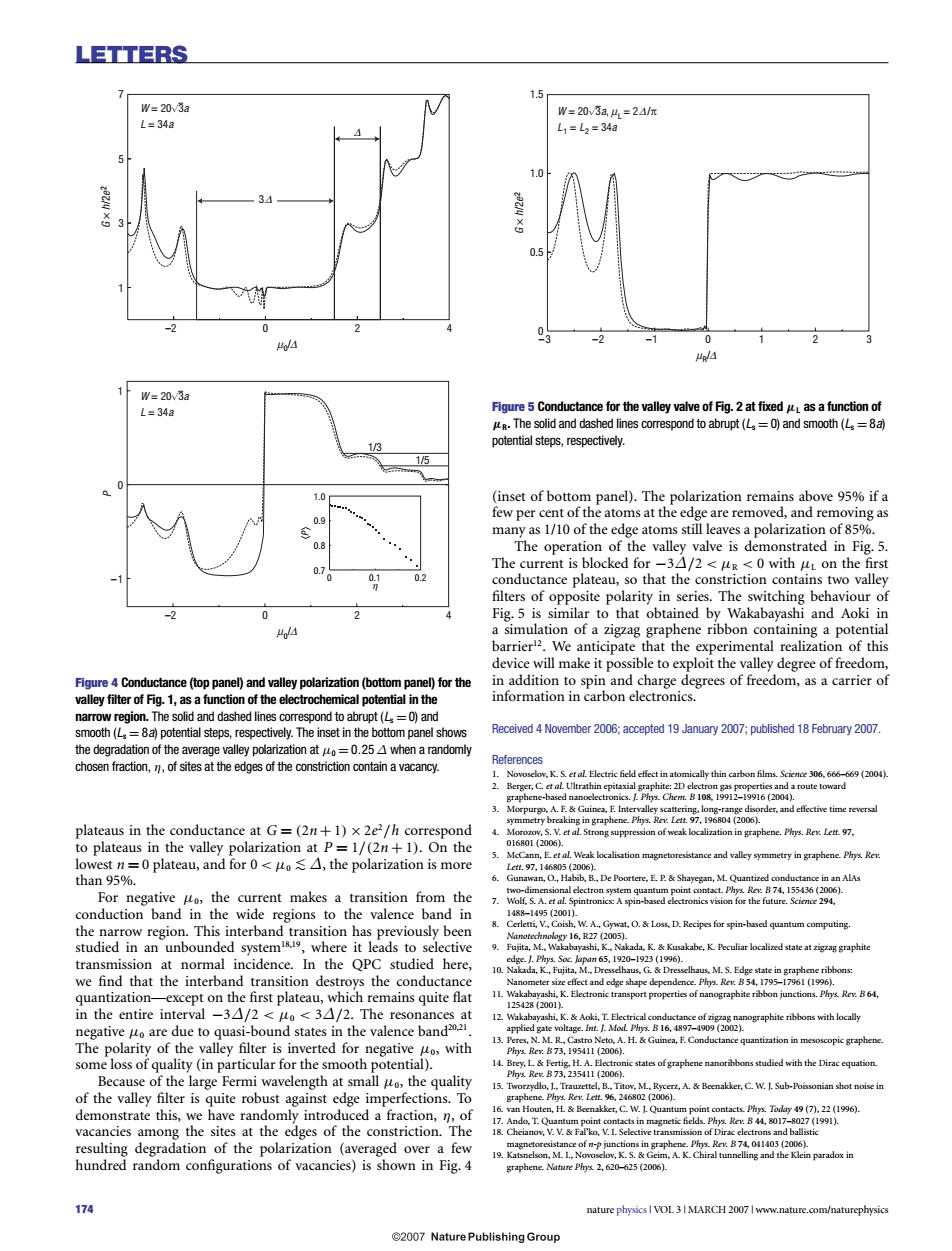
LETTERS 1.5 W=20v3a W=20v3a4=24/m L=34a L1=L2=34a 10 34 0.5 -2 0 HplA 1 W=20v3a L=34a Figure 5 Conductance for the valley valve of Fig.2 at fixed as a function of The solid and dashed lines correspond to abrupt(L=0)and smooth(L=8a) 13 potential steps,respectively. 1.0 (inset of bottom panel).The polarization remains above 95%if a 0.9 few per cent of the atoms at the edge are removed,and removing as many as 1/10 of the edge atoms still leaves a polarization of 85%. 0.8 The operation of the valley valve is demonstrated in Fig.5. 07 The current is blocked for-34/2<ug<0 with uL on the first 0 0.2 conductance plateau,so that the constriction contains two valley filters of opposite polarity in series.The switching behaviour of Fig.5 is similar to that obtained by Wakabayashi and Aoki in 4 a simulation of a zigzag graphene ribbon containing a potential barrier2.We anticipate that the experimental realization of this device will make it possible to exploit the valley degree of freedom, Figure 4 Conductance(top panel)and valley polarization (bottom panel)for the in addition to spin and charge degrees of freedom,as a carrier of valley filter of Fig.1,as a function of the electrochemical potential in the information in carbon electronics. narrow region.The solid and dashed lines correspond to abrupt(L0)and smooth(L=8a)potential steps,respectively.The inset in the bottom panel shows Received 4 November 2006:accepted 19 January 2007;published 18 February 2007. the degradation of the average valley polarization at o=0.25 A when a randomly chosen fraction,n,of sites at the edges of the constriction contain a vacancy. References 2.Berger,C.epitaxial graphite:2D electron gas properties and aroute toward graphene-based nanoelectronics.J.Phrys.Chent.B 108,19912-19916(2004). 3.Morpurgo.A.E&Guinea,E Intervalley scattering.long-range disorder,and effective time reversal plateaus in the conductance at G=(2n+1)x 2e2/h correspond S.V.et al Strong suppre to plateaus in the valley polarization at P=1/(2n+1).On the 016801(2006) 5. MeCann,E et al.Weak localisation magn resistance and valley symmetry in graphene.Phys.Rev. lowest n=0 plateau,and for0<uo≤△，the polarization is more Lctt.97.146805（20061. than 95%. 6. an.O..Habib.B..De Po n.M.Quantized conductance in an AlAs t Phys.RB74,155436(2D06) For negative wo,the current makes a transition from the electron syste 7. Wolf,S.A.et al.Spintronics:A spi based electronics vision for the future.Science 294. conduction band in the wide regions to the valence band in 1488-1495(2001). the narrow region.This interband transition has previously been 8.Cerletti,V.,Coish,W.A..Gywat,O.Le s.D.Recipes for spin-based quantum computing. studied in an unbounded system!s,where it leads to selective 9. ayashi.K e,K Peculiar localized state at zigzag graphite transmission at normal incidence.In the QPC studied here, cdge.k.%ys.Soc.Japan65,1920-1923(1996). 10.Nakada,K.,Fujita,M..Dresselhaus,G.Dresselhaus,M.S.Edge state in graphene ribbons: we find that the interband transition destroys the conductance Nanometer size effect and edge shape dependence.Phys.Rev:B54,1795-17961(1996). quantization-except on the first plateau,which remains quite flat 11.Wakab K.Elec nographite ribbon junctions.Plrys Rev.B64 254282001- in the entire interval -34/2<o<34/2.The resonances at 12 Wakabayashi.K.Aoki,T.Electrical conductance of zigzag nanographite ribbons with locally negative o are due to quasi-bound states in the valence band2021. applied gate voltage.Int..Mod.Phys.B16,4897-4909 (2002). The polarity of the valley filter is inverted for negative Ho,with 13. es,N.M.R.C Neto.A.H&Guin ea,F.Conductance quantization in mesoscopic graphene (2006). some loss of quality (in particular for the smooth potential). l4Brey,L&Fertig.H.A.过ectronic states ofg时 nanoribbons studied with the Dirac equation. Because of the large Fermi wavelength at small uo,the quality Plrys.Rev.B73,235411(2006). 15.Tworzydlo,I.Trauzettel,B..Titow,M..Ry z.A.Beenakker,C.W.I.Sub-Poissonian shot noise in of the valley filter is quite robust against edge imperfections.To he Rev Lett 96 746802 (20061 demonstrate this,we have randomly introduced a fraction,n,of 16.van Houten,H Beenakker,C.W.I.Quantum point contacts.Phys.Today 49(7).22(1996) 17.Ando.T.Quantum point contacts in magnetic fields.Phys.Rev.B 44,8017-8027(1991). vacancies among the sites at the edges of the constriction.The 18.Cheianov,V.V.&Fal'ko,V.I.Selective transmission of Dirac electrons and ballistic resulting degradation of the polarization (averaged over a few e.Phs.R.B74,041403(2006. A K.Chiral ling and the Klein paradox in hundred random configurations of vacancies)is shown in Fig.4 graphene.Nature Phy's.2,620-625 (2006). 174 nature physics I VOL 3 MARCH 2007 I www.nature.com/naturephysics 2007 Nature Publishing GroupLETTERS –2 0 1 3 5 7 2 4 μ Δ0/ μ Δ0/ –2 0 0 0.7 0.8 0.9 1.0 0.1 0.2 2 4 G × h/2e2 W = 20 3a L = 34a W = 20 3a L = 34a 3 Δ Δ –1 0 1 P η 〈P〉 1/3 1/5 Figure 4 Conductance (top panel) and valley polarization (bottom panel) for the valley filter of Fig. 1, as a function of the electrochemical potential in the narrow region. The solid and dashed lines correspond to abrupt (Ls = 0) and smooth (Ls = 8a) potential steps, respectively. The inset in the bottom panel shows the degradation of the average valley polarization at μ0 = 0.25 Δ when a randomly chosen fraction, η, of sites at the edges of the constriction contain a vacancy. plateaus in the conductance at G = (2n +1) ×2e2 /h correspond to plateaus in the valley polarization at P = 1/(2n + 1). On the lowest n = 0 plateau, and for 0 < μ0 ∼ < Δ, the polarization is more than 95%. For negative μ0, the current makes a transition from the conduction band in the wide regions to the valence band in the narrow region. This interband transition has previously been studied in an unbounded system18,19, where it leads to selective transmission at normal incidence. In the QPC studied here, we find that the interband transition destroys the conductance quantization—except on the first plateau, which remains quite flat in the entire interval −3Δ/2 < μ0 < 3Δ/2. The resonances at negative μ0 are due to quasi-bound states in the valence band20,21. The polarity of the valley filter is inverted for negative μ0, with some loss of quality (in particular for the smooth potential). Because of the large Fermi wavelength at small μ0, the quality of the valley filter is quite robust against edge imperfections. To demonstrate this, we have randomly introduced a fraction, η, of vacancies among the sites at the edges of the constriction. The resulting degradation of the polarization (averaged over a few hundred random configurations of vacancies) is shown in Fig. 4 –3 –2 –1 0 0 0.5 1.0 1.5 123 μ ΔR/ μ Δ L = 2 G × h/2e2 W = 20 3a, L1 = L2 = 34a /π Figure 5 Conductance for the valley valve of Fig. 2 at fixed μL as a function of μR. The solid and dashed lines correspond to abrupt (Ls = 0) and smooth (Ls = 8a) potential steps, respectively. (inset of bottom panel). The polarization remains above 95% if a few per cent of the atoms at the edge are removed, and removing as many as 1/10 of the edge atoms still leaves a polarization of 85%. The operation of the valley valve is demonstrated in Fig. 5. The current is blocked for −3Δ/2 < μR < 0 with μL on the first conductance plateau, so that the constriction contains two valley filters of opposite polarity in series. The switching behaviour of Fig. 5 is similar to that obtained by Wakabayashi and Aoki in a simulation of a zigzag graphene ribbon containing a potential barrier12. We anticipate that the experimental realization of this device will make it possible to exploit the valley degree of freedom, in addition to spin and charge degrees of freedom, as a carrier of information in carbon electronics. Received 4 November 2006; accepted 19 January 2007; published 18 February 2007. References 1. Novoselov, K. S. et al. Electric field effect in atomically thin carbon films. Science 306, 666–669 (2004). 2. Berger, C. et al. Ultrathin epitaxial graphite: 2D electron gas properties and a route toward graphene-based nanoelectronics. J. Phys. Chem. B 108, 19912–19916 (2004). 3. Morpurgo, A. F. & Guinea, F. Intervalley scattering, long-range disorder, and effective time reversal symmetry breaking in graphene. Phys. Rev. Lett. 97, 196804 (2006). 4. Morozov, S. V. et al. Strong suppression of weak localization in graphene. Phys. Rev. Lett. 97, 016801 (2006). 5. McCann, E. et al. Weak localisation magnetoresistance and valley symmetry in graphene. Phys. Rev. Lett. 97, 146805 (2006). 6. Gunawan, O., Habib, B., De Poortere, E. P. & Shayegan, M. Quantized conductance in an AlAs two-dimensional electron system quantum point contact. Phys. Rev. B 74, 155436 (2006). 7. Wolf, S. A. et al. Spintronics: A spin-based electronics vision for the future. Science 294, 1488–1495 (2001). 8. Cerletti, V., Coish, W. A., Gywat, O. & Loss, D. Recipes for spin-based quantum computing. Nanotechnology 16, R27 (2005). 9. Fujita, M., Wakabayashi, K., Nakada, K. & Kusakabe, K. Peculiar localized state at zigzag graphite edge. J. Phys. Soc. Japan 65, 1920–1923 (1996). 10. Nakada, K., Fujita, M., Dresselhaus, G. & Dresselhaus, M. S. Edge state in graphene ribbons: Nanometer size effect and edge shape dependence. Phys. Rev. B 54, 1795–17961 (1996). 11. Wakabayashi, K. Electronic transport properties of nanographite ribbon junctions. Phys. Rev. B 64, 125428 (2001). 12. Wakabayashi, K. & Aoki, T. Electrical conductance of zigzag nanographite ribbons with locally applied gate voltage. Int. J. Mod. Phys. B 16, 4897–4909 (2002). 13. Peres, N. M. R., Castro Neto, A. H. & Guinea, F. Conductance quantization in mesoscopic graphene. Phys. Rev. B 73, 195411 (2006). 14. Brey, L. & Fertig, H. A. Electronic states of graphene nanoribbons studied with the Dirac equation. Phys. Rev. B 73, 235411 (2006). 15. Tworzydło, J., Trauzettel, B., Titov, M., Rycerz, A. & Beenakker, C. W. J. Sub-Poissonian shot noise in graphene. Phys. Rev. Lett. 96, 246802 (2006). 16. van Houten, H. & Beenakker, C. W. J. Quantum point contacts. Phys. Today 49 (7), 22 (1996). 17. Ando, T. Quantum point contacts in magnetic fields. Phys. Rev. B 44, 8017–8027 (1991). 18. Cheianov, V. V. & Fal’ko, V. I. Selective transmission of Dirac electrons and ballistic magnetoresistance of n-p junctions in graphene. Phys. Rev. B 74, 041403 (2006). 19. Katsnelson, M. I., Novoselov, K. S. & Geim, A. K. Chiral tunnelling and the Klein paradox in graphene. Nature Phys. 2, 620–625 (2006). 174 nature physics VOL 3 MARCH 2007 www.nature.com/naturephysics Untitled-1 3 13/2/07, 12:35:55 pm