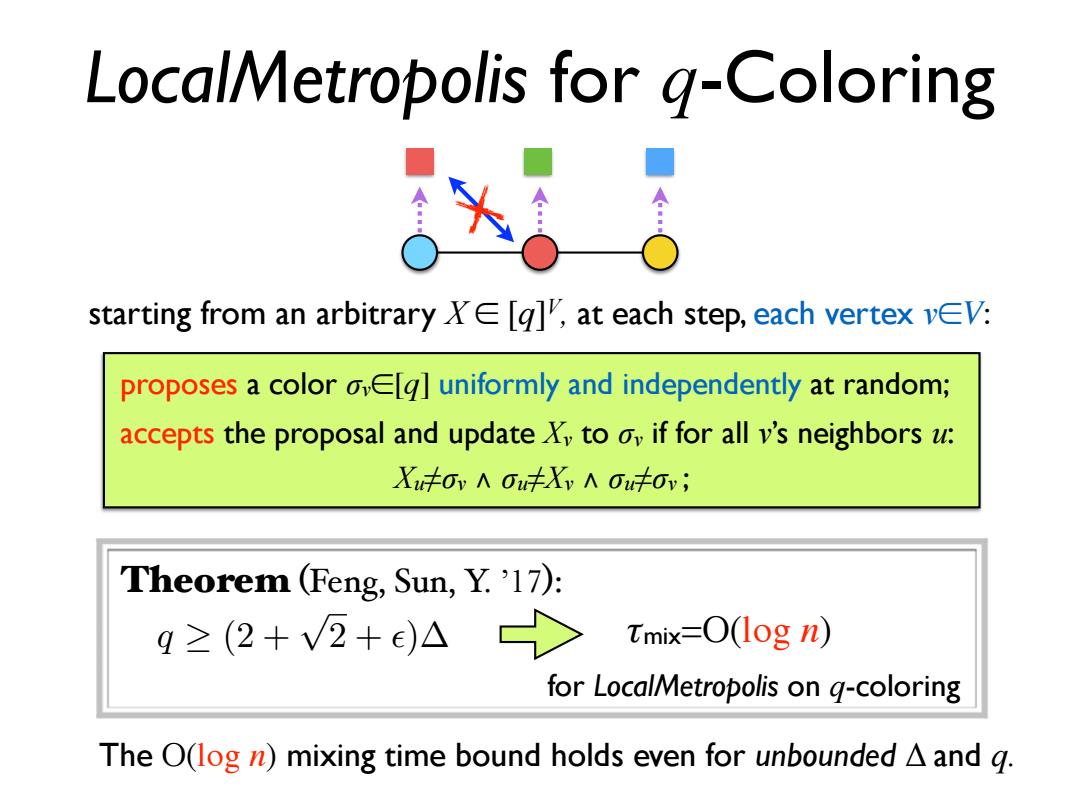
LocalMetropolis for q-Coloring starting from an arbitrary XE [g],at each step,each vertex vEV: proposes a color ovE[g]uniformly and independently at random; accepts the proposal and update X to oy if for all v's neighbors u: X≠0vAOu≠X,NOu≠0； Theorem (Feng,Sun,Y.'17): q≥(2+V2+e)△> Tmix=O(log n) for LocalMetropolis on g-coloring The O(log n)mixing time bound holds even for unbounded A and g.LocalMetropolis for q-Coloring starting from an arbitrary X ∈ [q]V , at each step, each vertex v∈V: proposes a color σv∈[q] uniformly and independently at random; accepts the proposal and update Xv to σv if for all v’s neighbors u: Xu≠σv ∧ σu≠Xv ∧ σu≠σv ; The O(log n) mixing time bound holds even for unbounded Δ and q. Theorem (Feng, Sun, Y. ’17): q ￾ (2 + τmix=O(log n) p 2 + ✏)￾ for LocalMetropolis on q-coloring