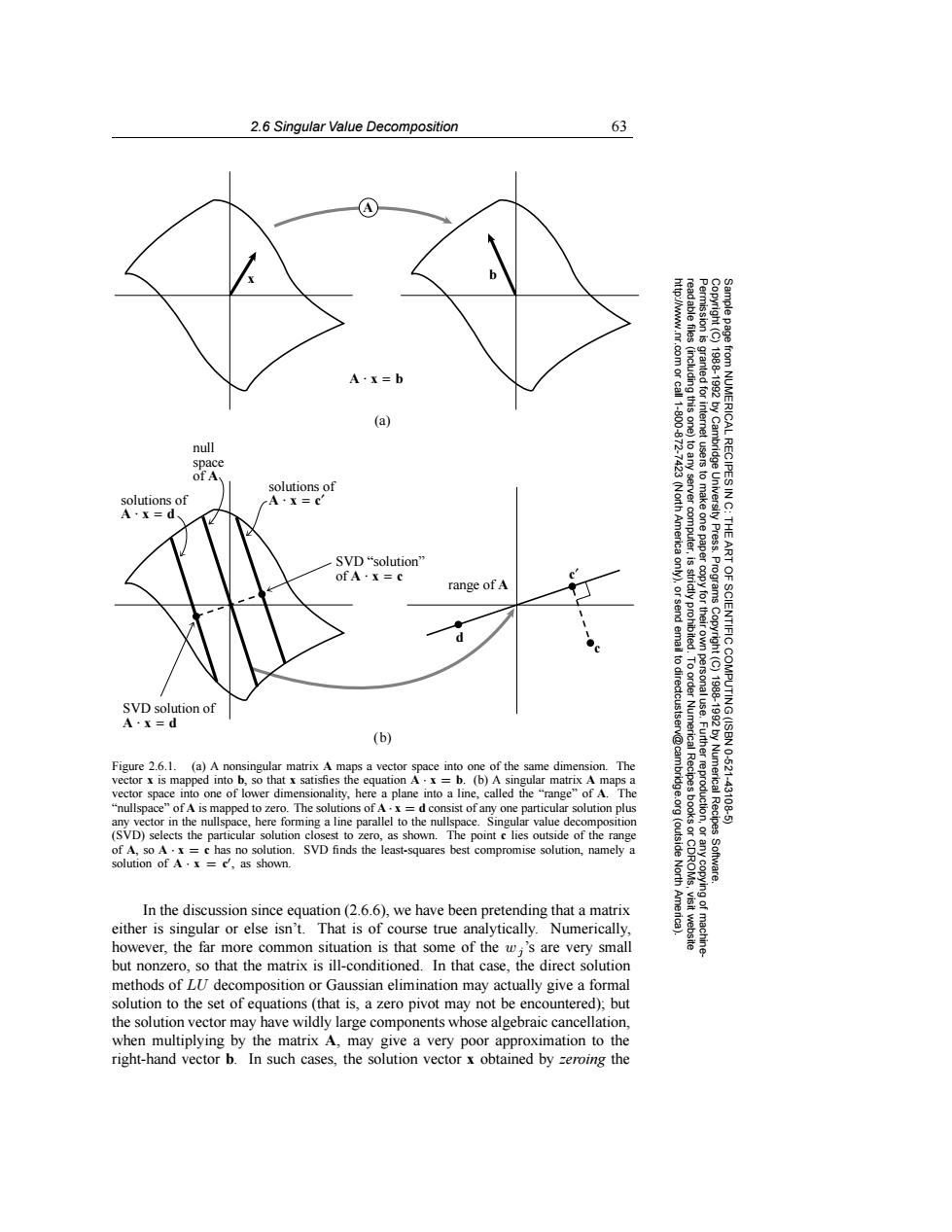
2.6 Singular Value Decomposition 63 A A·x=b mnttt granted for (a) (including this one) interne null /Cambridge space solutions of n NUMERICAL RECIPES IN C: solutions of A·X=c A·X=d -7423 (North America to any server computer, uae us e University Press. THE SVD“solution" ofA·X=c 是 range of A send d st st copyfor thei Programs to dir Copyright (C) SVD solution of ART OF SCIENTIFIC COMPUTING(ISBN A·x=d (b) v@cam Figure 2.6.1.(a)A nonsingular matrix A maps a vector space into one of the same dimension.The 1988-1992 by Numerical Recipes 10-621 vector x is mapped into b,so that x satisfies the equation A.x b.(b)A singular matrix A maps a vector space into one of lower dimensionality,here a plane into a line,called the "range"of A.The "nullspace"of A is mapped to zero.The solutions of A.x d consist of any one particular solution plus 43108.5 any vector in the nullspace,here forming a line parallel to the nullspace.Singular value decomposition (SVD)selects the particular solution closest to zero,as shown.The point c lies outside of the range of A,so A.x =c has no solution.SVD finds the least-squares best compromise solution,namely a (outside 膜 solution of A.x ='as shown. North Software. In the discussion since equation(2.6.6).we have been pretending that a matrix either is singular or else isn't.That is of course true analytically.Numerically visit website however,the far more common situation is that some of the w;'s are very small machine but nonzero,so that the matrix is ill-conditioned.In that case,the direct solution methods of LU decomposition or Gaussian elimination may actually give a formal solution to the set of equations(that is,a zero pivot may not be encountered);but the solution vector may have wildly large components whose algebraic cancellation. when multiplying by the matrix A,may give a very poor approximation to the right-hand vector b.In such cases,the solution vector x obtained by zeroing the2.6 Singular Value Decomposition 63 Permission is granted for internet users to make one paper copy for their own personal use. Further reproduction, or any copyin Copyright (C) 1988-1992 by Cambridge University Press. Programs Copyright (C) 1988-1992 by Numerical Recipes Software. Sample page from NUMERICAL RECIPES IN C: THE ART OF SCIENTIFIC COMPUTING (ISBN 0-521-43108-5) g of machine￾readable files (including this one) to any server computer, is strictly prohibited. To order Numerical Recipes books or CDROMs, visit website http://www.nr.com or call 1-800-872-7423 (North America only), or send email to directcustserv@cambridge.org (outside North America). A ⋅ x = b SVD “solution” of A ⋅ x = c solutions of solutions of A ⋅ x = c′ A ⋅ x = d null space of A SVD solution of A ⋅ x = d range of A d c (b) (a) A x b c′ Figure 2.6.1. (a) A nonsingular matrix A maps a vector space into one of the same dimension. The vector x is mapped into b, so that x satisfies the equation A · x = b. (b) A singular matrix A maps a vector space into one of lower dimensionality, here a plane into a line, called the “range” of A. The “nullspace” of A is mapped to zero. The solutions of A · x = d consist of any one particular solution plus any vector in the nullspace, here forming a line parallel to the nullspace. Singular value decomposition (SVD) selects the particular solution closest to zero, as shown. The point c lies outside of the range of A, so A · x = c has no solution. SVD finds the least-squares best compromise solution, namely a solution of A · x = c
, as shown. In the discussion since equation (2.6.6), we have been pretending that a matrix either is singular or else isn’t. That is of course true analytically. Numerically, however, the far more common situation is that some of the wj ’s are very small but nonzero, so that the matrix is ill-conditioned. In that case, the direct solution methods of LU decomposition or Gaussian elimination may actually give a formal solution to the set of equations (that is, a zero pivot may not be encountered); but the solution vector may have wildly large components whose algebraic cancellation, when multiplying by the matrix A, may give a very poor approximation to the right-hand vector b. In such cases, the solution vector x obtained by zeroing the