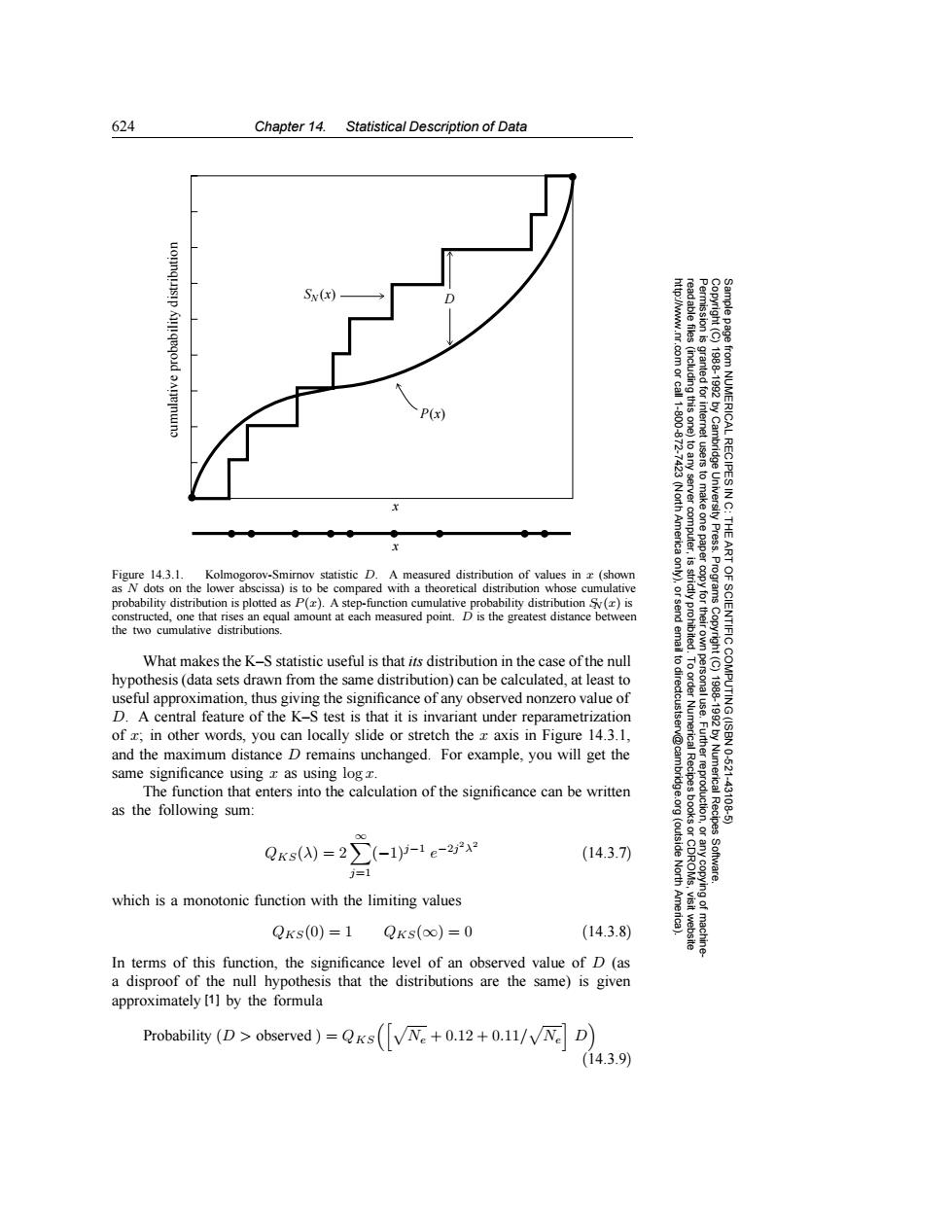
624 Chapter 14.Statistical Description of Data Sv(x) read able files 人 P(x) http://www.nr.com or call 1-800-872- (including this one) to any server computer, -7423 (North America tusers to make one paper 1988-1992 by Cambridge University Press. from NUMERICAL RECIPES IN C: THE Figure 14.3.1.Kolmogorov-Smirnov statistic D.A measured distribution of values in x (shown only). as N dots on the lower abscissa)is to be compared with a theoretical distribution whose cumulative ictly proh Programs probability distribution is plotted as P().A step-function cumulative probability distribution ()is constructed,one that rises an equal amount at each measured point.D is the greatest distance between the two cumulative distributions. What makes the K-S statistic useful is that its distribution in the case of the null to dir hypothesis(data sets drawn from the same distribution)can be calculated,at least to useful approximation,thus giving the significance of any observed nonzero value of ART OF SCIENTIFIC COMPUTING (ISBN D.A central feature of the K-S test is that it is invariant under reparametrization 1988-19920 of r;in other words,you can locally slide or stretch the z axis in Figure 14.3.1, and the maximum distance D remains unchanged.For example,you will get the same significance using x as using log r. 10-521 The function that enters into the calculation of the significance can be written as the following sum: Numerical Recipes 43198-5 Qks(A)=2 -1-1e-2212 (14.3.7) (outside j=1 North Software. which is a monotonic function with the limiting values QKs(0)=1QKs(∞)=0 (14.3.8) visit website machine In terms of this function,the significance level of an observed value of D(as a disproof of the null hypothesis that the distributions are the same)is given approximately [1]by the formula Probability(D>observed)=Qks(N+.12+0.11/N D 14.3.9624 Chapter 14. Statistical Description of Data Permission is granted for internet users to make one paper copy for their own personal use. Further reproduction, or any copyin Copyright (C) 1988-1992 by Cambridge University Press. Programs Copyright (C) 1988-1992 by Numerical Recipes Software. Sample page from NUMERICAL RECIPES IN C: THE ART OF SCIENTIFIC COMPUTING (ISBN 0-521-43108-5) g of machine￾readable files (including this one) to any server computer, is strictly prohibited. To order Numerical Recipes books or CDROMs, visit website http://www.nr.com or call 1-800-872-7423 (North America only), or send email to directcustserv@cambridge.org (outside North America). x x D P(x) SN (x) cumulative probability distribution Figure 14.3.1. Kolmogorov-Smirnov statistic D. A measured distribution of values in x (shown as N dots on the lower abscissa) is to be compared with a theoretical distribution whose cumulative probability distribution is plotted as P(x). A step-function cumulative probability distribution SN (x) is constructed, one that rises an equal amount at each measured point. D is the greatest distance between the two cumulative distributions. What makes the K–S statistic useful is that its distribution in the case of the null hypothesis (data sets drawn from the same distribution) can be calculated, at least to useful approximation, thus giving the significance of any observed nonzero value of D. A central feature of the K–S test is that it is invariant under reparametrization of x; in other words, you can locally slide or stretch the x axis in Figure 14.3.1, and the maximum distance D remains unchanged. For example, you will get the same significance using x as using log x. The function that enters into the calculation of the significance can be written as the following sum: QKS(λ)=2
∞ j=1 (−1)j−1 e−2j2λ2 (14.3.7) which is a monotonic function with the limiting values QKS(0) = 1 QKS(∞)=0 (14.3.8) In terms of this function, the significance level of an observed value of D (as a disproof of the null hypothesis that the distributions are the same) is given approximately [1] by the formula Probability (D > observed ) = QKSNe + 0.12 + 0.11/ Ne  D  (14.3.9)