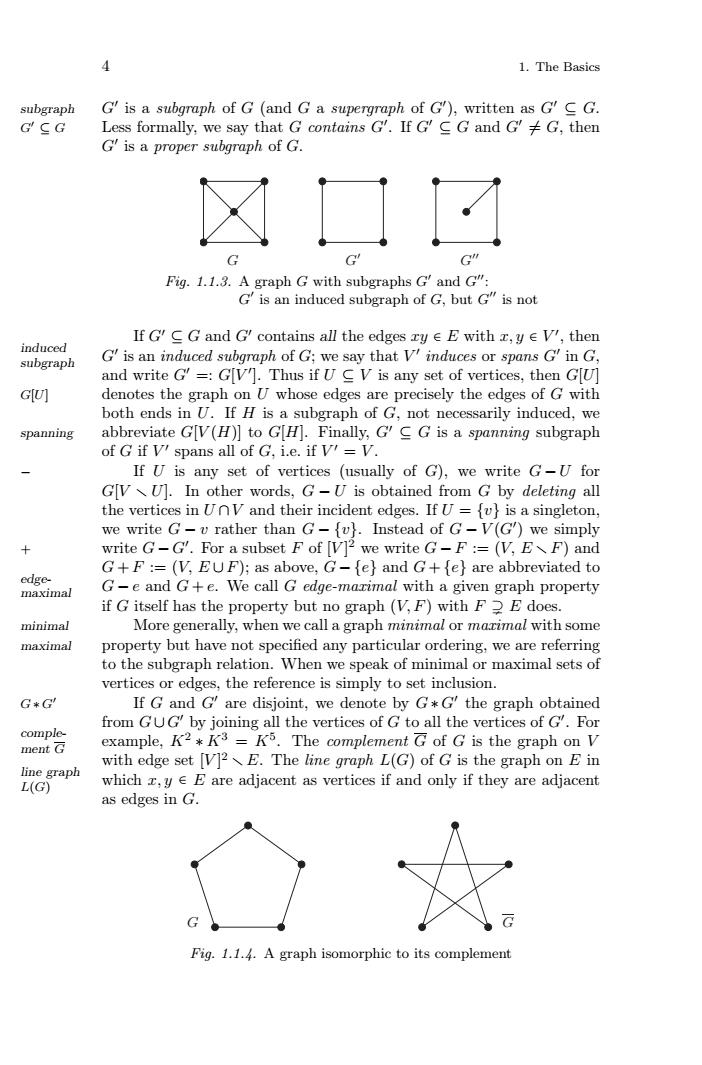
1. The Basics4G' is a subgraph of G (and G a supergraph of G'), written as G' C GsubgraphLess formally, we say that G contains G'. If G' C G and G' + G, thenG'CGG' is a proper subgraph of G.区口口Fig. 1.1.3. A graph G with subgraphs G' and G":G' is an induced subgraph of G, but G" is notIf G' C G and G' contains all the edges ry e E with ,y e V', theninducedG' is an induced subgraph of G; we say that V' induces or spans G' in Gsubgraphand write G' =: G[V']. Thus if U C V is any set of vertices, then G[U]G]denotes the graphU whose edges are precisely the edges of G withboth ends in U. If H is aa subgraph of G,not necesessarilyinduced.weabbreviate G[V(H)] to G[H], Finally, G' C G is a spanning subgraphspanningof G if Vi spans all of G, i.e. if VI = V.If U is any set of vertices (usually of G), we write G-U forG[V U]. In other words, G- U is obtained from G by deleting allthe vertices in UnV and their incident edges. If U = (u) is a singleton,wewriteGu rather than G - [u). Instead of G - V(G') we simplywriteG-GFoAsubsetFof[V2wewriteG-F:=(V.EF)and+G+F := (V, EUF); as above, G- (e]) and G+[e) are abbreviated toedleimalG- and G+e. We call G edge-mazimal with a given graph propertyif G itself has the property but no graph (V,F) with F2 E doesminimalMoregenerally,wlhenwecallagraphminimalormarimalwithsomeproperty but have not specified any particular ordering, we are referringmaximalto the subgraph relation.When we speak of minimal or maximal sets ofvertices es, the reference is simply to set inclusionIf G and G' are disjoinnt, we denote by G*G' the graph obtainG*G'from GUG' by joining all the vertices of G to all the vertices of G'. Folcompleexample, K?+ K3 - K. The complement C of G is the graph on Vment Gwith edge set [V]? E. The line graph L(G) of G is the graph on E inLegmaphwhich ,y e E are adjacent as vertices if and only if they are adjacentas edges inGFig. 1.1.4. A graph isomorphic to its complement4 1. The Basics G is a subgraph of G (and G a supergraph of G subgraph ), written as G ⊆ G. Less formally, we say that G contains G . If G ⊆ G and G G = G, then ⊆ G G is a proper subgraph of G. G G G Fig. 1.1.3. A graph G with subgraphs G and G: G is an induced subgraph of G, but G is not If G ⊆ G and G contains all the edges xy ∈ E with x, y ∈ V , then G is an induced subgraph of G; we say that V induces or spans G in G, induced subgraph and write G =: G[V ]. Thus if U ⊆ V is any set of vertices, then G[U] G[U] denotes the graph on U whose edges are precisely the edges of G with both ends in U. If H is a subgraph of G, not necessarily induced, we spanning abbreviate G[V (H)] to G[H]. Finally, G ⊆ G is a spanning subgraph of G if V spans all of G, i.e. if V = V . − If U is any set of vertices (usually of G), we write G − U for G[V U]. In other words, G − U is obtained from G by deleting all the vertices in U ∩V and their incident edges. If U = {v} is a singleton, we write G − v rather than G − {v}. Instead of G − V (G ) we simply write G − G . For a subset F of [V ] 2 + we write G − F := (V, E F) and G + F := (V, E ∪F); as above, G − {e} and G + {e} are abbreviated to G − e and G + e. We call G edge-maximal with a given graph property edge￾maximal if G itself has the property but no graph (V,F) with F E does. minimal More generally, when we call a graph minimal or maximal with some maximal property but have not specified any particular ordering, we are referring to the subgraph relation. When we speak of minimal or maximal sets of vertices or edges, the reference is simply to set inclusion. If G and G are disjoint, we denote by G ∗ G G ∗ G the graph obtained from G∪G by joining all the vertices of G to all the vertices of G . For example, K2 ∗ K3 = K5. The complement G of G is the graph on V comple￾ment G with edge set [V ] 2 E. The line graph L(G) of G is the graph on E in which x, y ∈ E are adjacent as vertices if and only if they are adjacent line graph L(G) as edges in G. G G Fig. 1.1.4. A graph isomorphic to its complement