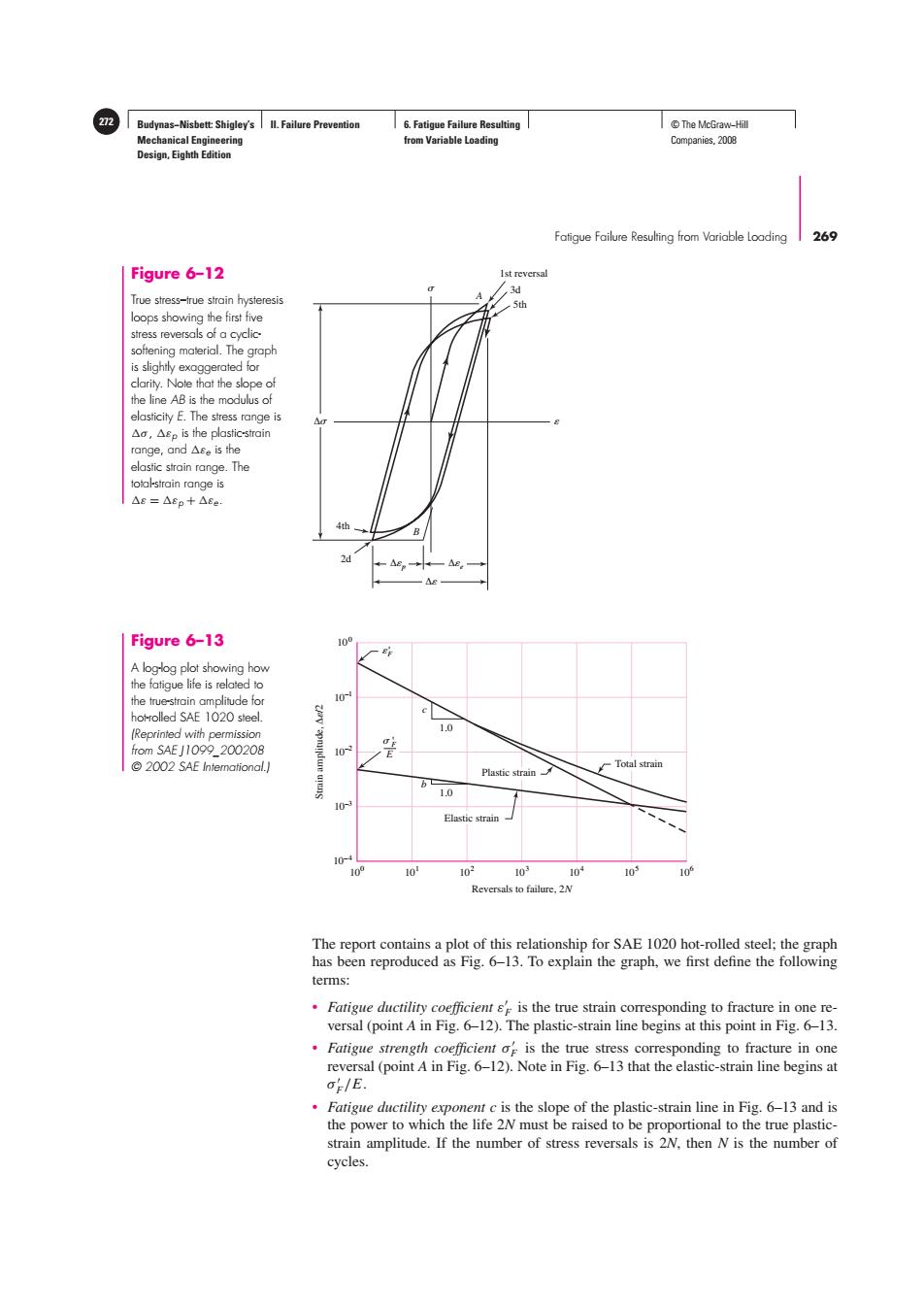
Budynas-Nisbett:Shigley's ll.Failure Prevention 6.Fatigue Failure Resulting ©The McGraw-Hil Mechanical Engineering from Variable Loading Companies,2008 Design,Eighth Edition Fatigue Failure Resulting from Variable Loading 269 Figure 6-12 Ist reversal ,3d True stress-true strain hysteresis .5th loops showing the first five stress reversals of a cyclic softening material.The graph is slightly exaggerated for clarity.Note that the slope of the line AB is the modulus of elasticity E.The stress range is △a,△ep is the plastic-strain range,.and△Se is the elastic strain range.The total-strain range is △g=△Ep+△Ee Figure 6-13 o A loglog plot showing how the fatigue life is related to the true-strain amplitude for 10 hot-rolled SAE 1020 steel. (Reprinted with permission 1.0 from SAE J1099_200208 0N 2002 SAE Intemational.] Plastic strain Total strain 1.0 10 Elastic strain 10 10 10 102 103 104 103 10 Reversals to failure,2N The report contains a plot of this relationship for SAE 1020 hot-rolled steel:the graph has been reproduced as Fig.6-13.To explain the graph,we first define the following terms: Fatigue ductility coefficient s is the true strain corresponding to fracture in one re- versal (point A in Fig.6-12).The plastic-strain line begins at this point in Fig.6-13. Fatigue strength coefficient of is the true stress corresponding to fracture in one reversal (point A in Fig.6-12).Note in Fig.6-13 that the elastic-strain line begins at o/E. Fatigue ductility exponent c is the slope of the plastic-strain line in Fig.6-13 and is the power to which the life 2N must be raised to be proportional to the true plastic- strain amplitude.If the number of stress reversals is 2N,then N is the number of cycles.Budynas−Nisbett: Shigley’s Mechanical Engineering Design, Eighth Edition II. Failure Prevention 6. Fatigue Failure Resulting from Variable Loading 272 © The McGraw−Hill Companies, 2008 Fatigue Failure Resulting from Variable Loading 269 4th 2d 1st reversal 3d 5th A B Δ Δp Δe Δ Figure 6–12 True stress–true strain hysteresis loops showing the first five stress reversals of a cyclic￾softening material. The graph is slightly exaggerated for clarity. Note that the slope of the line AB is the modulus of elasticity E. The stress range is σ , εp is the plastic-strain range, and εe is the elastic strain range. The total-strain range is ε = εp + εe. The report contains a plot of this relationship for SAE 1020 hot-rolled steel; the graph has been reproduced as Fig. 6–13. To explain the graph, we first define the following terms: • Fatigue ductility coefficient ε F is the true strain corresponding to fracture in one re￾versal (point A in Fig. 6–12). The plastic-strain line begins at this point in Fig. 6–13. • Fatigue strength coefficient σ F is the true stress corresponding to fracture in one reversal (point A in Fig. 6–12). Note in Fig. 6–13 that the elastic-strain line begins at σ F /E. • Fatigue ductility exponent c is the slope of the plastic-strain line in Fig. 6–13 and is the power to which the life 2N must be raised to be proportional to the true plastic￾strain amplitude. If the number of stress reversals is 2N, then N is the number of cycles. 100 10–4 10–3 10–2 10–1 100 101 102 103 104 105 106 Reversals to failure, 2N Strain amplitude, Δ/2 ' F c 1.0 b 1.0 ' F E Total strain Plastic strain Elastic strain Figure 6–13 A log-log plot showing how the fatigue life is related to the true-strain amplitude for hot-rolled SAE 1020 steel. (Reprinted with permission from SAE J1099_200208 © 2002 SAE International.)