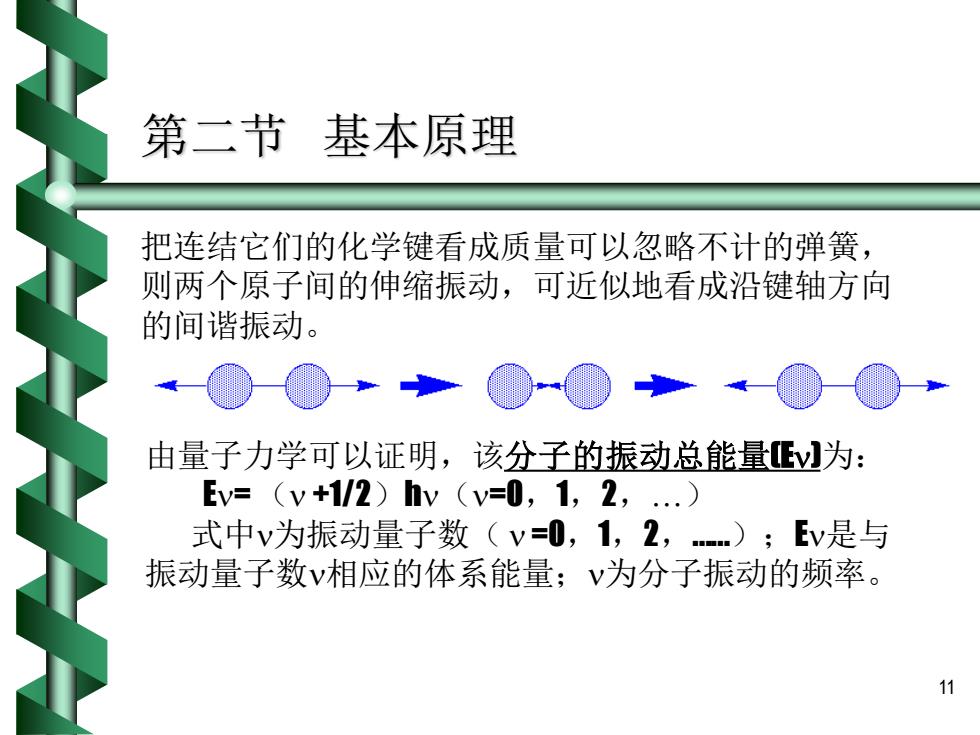
第二节基本原理 把连结它们的化学键看成质量可以忽略不计的弹簧， 则两个原子间的伸缩振动，可近似地看成沿键轴方向 的间谐振动。 由量子力学可以证明，该分子的振动总能量为： Ev=(v+1/2)hv(v=0,1,2,.) 式中v为振动量子数(v=0,1,2,);Ev是与 振动量子数v相应的体系能量；v为分子振动的频率。 11 11 第二节 基本原理 把连结它们的化学键看成质量可以忽略不计的弹簧， 则两个原子间的伸缩振动，可近似地看成沿键轴方向 的间谐振动。 由量子力学可以证明，该分子的振动总能量(E)为： E= （ +1/2）h（=0，1，2，） 式中为振动量子数（  =0，1，2，.）；E是与 振动量子数相应的体系能量；为分子振动的频率