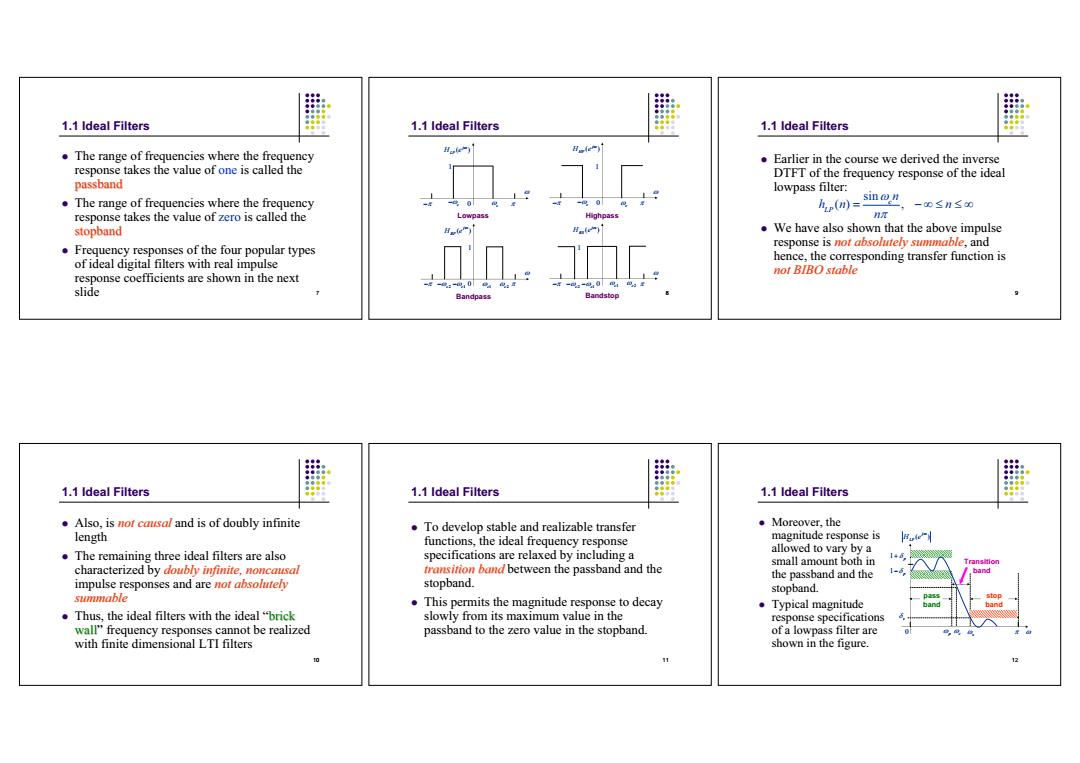
1.1 ldeal Filters 1.1 Ideal Filters 1.1 Ideal Filters The range of frequencies where the frequency H Earlier in the course we derived the inverse response takes the value of one is called the DTFT of the frequency response of the ideal passband lowpass filter: The range of frequencies where the frequency h(n)=sinon -0≤n≤0 response takes the value of zero is called the Lowpass Highpas stopband He) We have also shown that the above impulse Frequency responses of the four popular types of ideal digital filters with real impulse response coefficients are shown in the next . response is not absolutely summable,and hence,the corresponding transfer function is not BIBO stable slide 7 1.1 Ideal Filters 1.1 Ideal Filters 1.1 Ideal Filters Also,is not causal and is of doubly infinite .To develop stable and realizable transfer Moreover.the length functions,the ideal frequency response magnitude response is The remaining three ideal filters are also specifications are relaxed by including a allowed to vary by a small amount both in 146, characterized by doubly infinite,noncausal transition band between the passband and the the passband and the 1-6 impulse responses and are not absolutely stopband. stopband. summable This permits the magnitude response to decay ·Typical magnitude Thus,the ideal filters with the ideal "brick slowly from its maximum value in the response specifications wall"frequency responses cannot be realized passband to the zero value in the stopband. of a lowpass filter are with finite dimensional LTI filters shown in the figure.7 1.1 Ideal Filters The range of frequencies where the frequency response takes the value of one is called the passband The range of frequencies where the frequency response takes the value of zero is called the stopband Frequency responses of the four popular types of ideal digital filters with real impulse response coefficients are shown in the next slide 8 1.1 Ideal Filters ( ) j H e BS  0 1 Bandstop ( ) j H e LP c 0 c   1 Lowpass ( ) j H e HP c 0 c   1 Highpass ( ) j H e BP  0 c1 c2 1 Bandpass c2 c1 c2 c1 c1 c2 9 1.1 Ideal Filters Earlier in the course we derived the inverse DTFT of the frequency response of the ideal lowpass filter: We have also shown that the above impulse response is not absolutely not absolutely summable summable, and hence, the corresponding transfer function is not BIBO stable not BIBO stable sin () , c LP n hn n n    10 1.1 Ideal Filters Also, is not causal not causal and is of doubly infinite length The remaining three ideal filters are also characterized by doubly infinite, doubly infinite, noncausal noncausal impulse responses and are not absolutely not absolutely summable summable Thus, the ideal filters with the ideal “brick wall” frequency responses cannot be realized with finite dimensional LTI filters 11 1.1 Ideal Filters To develop stable and realizable transfer functions, the ideal frequency response specifications are relaxed by including a transition band between the passband and the stopband. This permits the magnitude response to decay slowly from its maximum value in the passband to the zero value in the stopband. 12 1.1 Ideal Filters Moreover, the magnitude response is allowed to vary by a small amount both in the passband and the stopband. Typical magnitude response specifications of a lowpass filter are shown in the figure. ( ) j HLP e 0 p s 1 p  1 p  s  c pass band stop band Transition band