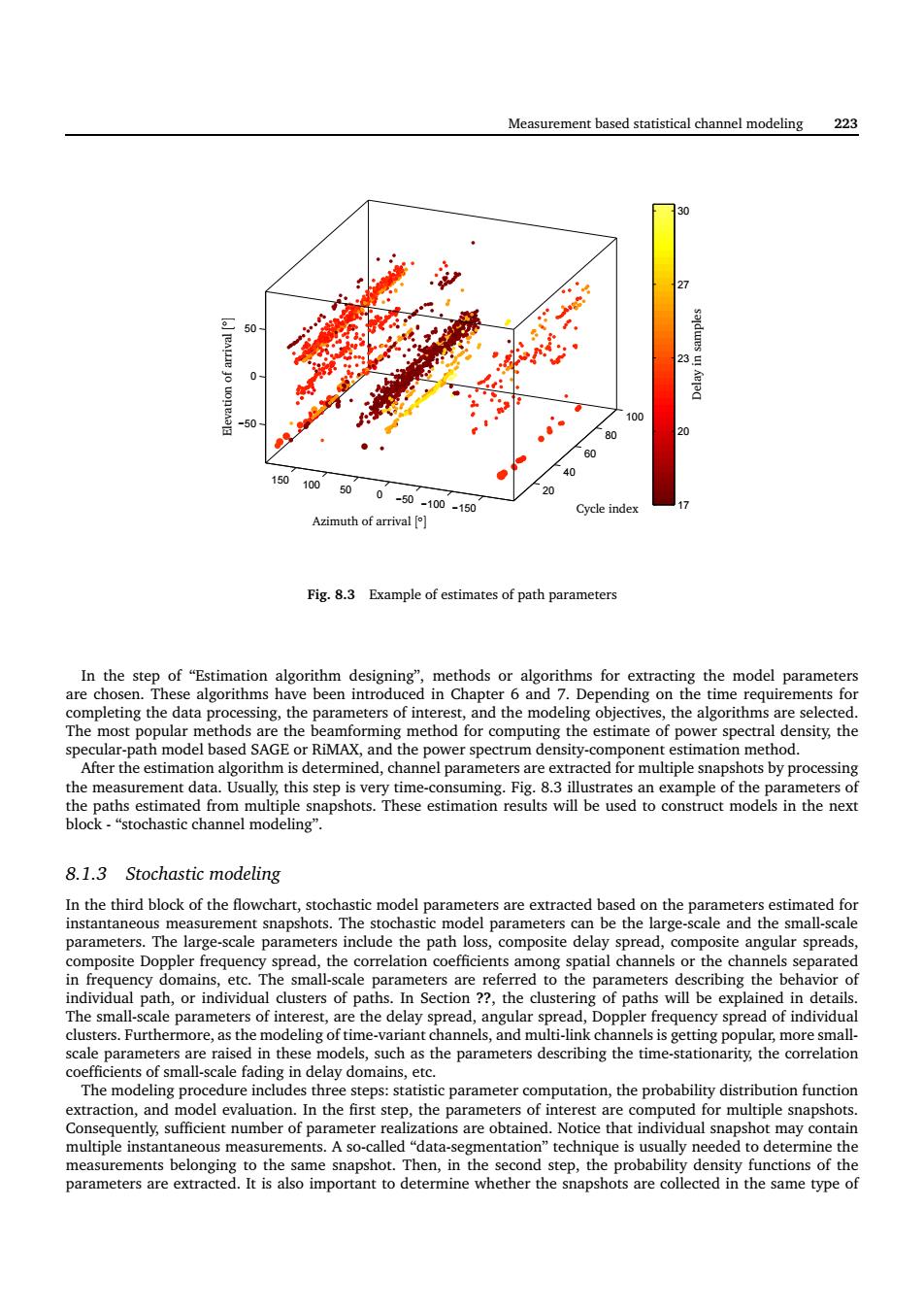
Measurement based statistical channel modeling 223 150100 50-100-150 Cycle index Azimuth of arrival Fig.8.3 Example of estimates of path parameters The most popular methods re the .channel parameters are extracted for mutiple snapshots by processing 8.1.3 Stochastic modeling parameters.The large-scale parameters include the path loss,composite delay spread com site angular spread lation coem efeaaot s.In Section ??the clustering of paths will be explained in details scale parame re raise n these ode s.such as the parameters describing the time-stationarity.the correlation coeteciemoieafgp extraction,and model evaluation.In the first step,the parameters of interest arec Notice that ind may con same snapshot.Then,the second stp the probabi den sity functions of th parameters are extract It is also important to determine whether the snapsho s are co in the same type oMeasurement based statistical channel modeling 223 20 40 60 80 100 −150 −100 −50 0 50 100 150 −50 0 50 17 20 23 27 30 Azimuth of arrival [ ◦ ] Elevation of arrival [ ◦ ] Cycle index Delay in samples Fig. 8.3 Example of estimates of path parameters In the step of “Estimation algorithm designing”, methods or algorithms for extracting the model parameters are chosen. These algorithms have been introduced in Chapter 6 and 7. Depending on the time requirements for completing the data processing, the parameters of interest, and the modeling objectives, the algorithms are selected. The most popular methods are the beamforming method for computing the estimate of power spectral density, the specular-path model based SAGE or RiMAX, and the power spectrum density-component estimation method. After the estimation algorithm is determined, channel parameters are extracted for multiple snapshots by processing the measurement data. Usually, this step is very time-consuming. Fig. 8.3 illustrates an example of the parameters of the paths estimated from multiple snapshots. These estimation results will be used to construct models in the next block - “stochastic channel modeling”. 8.1.3 Stochastic modeling In the third block of the flowchart, stochastic model parameters are extracted based on the parameters estimated for instantaneous measurement snapshots. The stochastic model parameters can be the large-scale and the small-scale parameters. The large-scale parameters include the path loss, composite delay spread, composite angular spreads, composite Doppler frequency spread, the correlation coefficients among spatial channels or the channels separated in frequency domains, etc. The small-scale parameters are referred to the parameters describing the behavior of individual path, or individual clusters of paths. In Section ??, the clustering of paths will be explained in details. The small-scale parameters of interest, are the delay spread, angular spread, Doppler frequency spread of individual clusters. Furthermore, as the modeling of time-variant channels, and multi-link channels is getting popular, more small￾scale parameters are raised in these models, such as the parameters describing the time-stationarity, the correlation coefficients of small-scale fading in delay domains, etc. The modeling procedure includes three steps: statistic parameter computation, the probability distribution function extraction, and model evaluation. In the first step, the parameters of interest are computed for multiple snapshots. Consequently, sufficient number of parameter realizations are obtained. Notice that individual snapshot may contain multiple instantaneous measurements. A so-called “data-segmentation” technique is usually needed to determine the measurements belonging to the same snapshot. Then, in the second step, the probability density functions of the parameters are extracted. It is also important to determine whether the snapshots are collected in the same type of