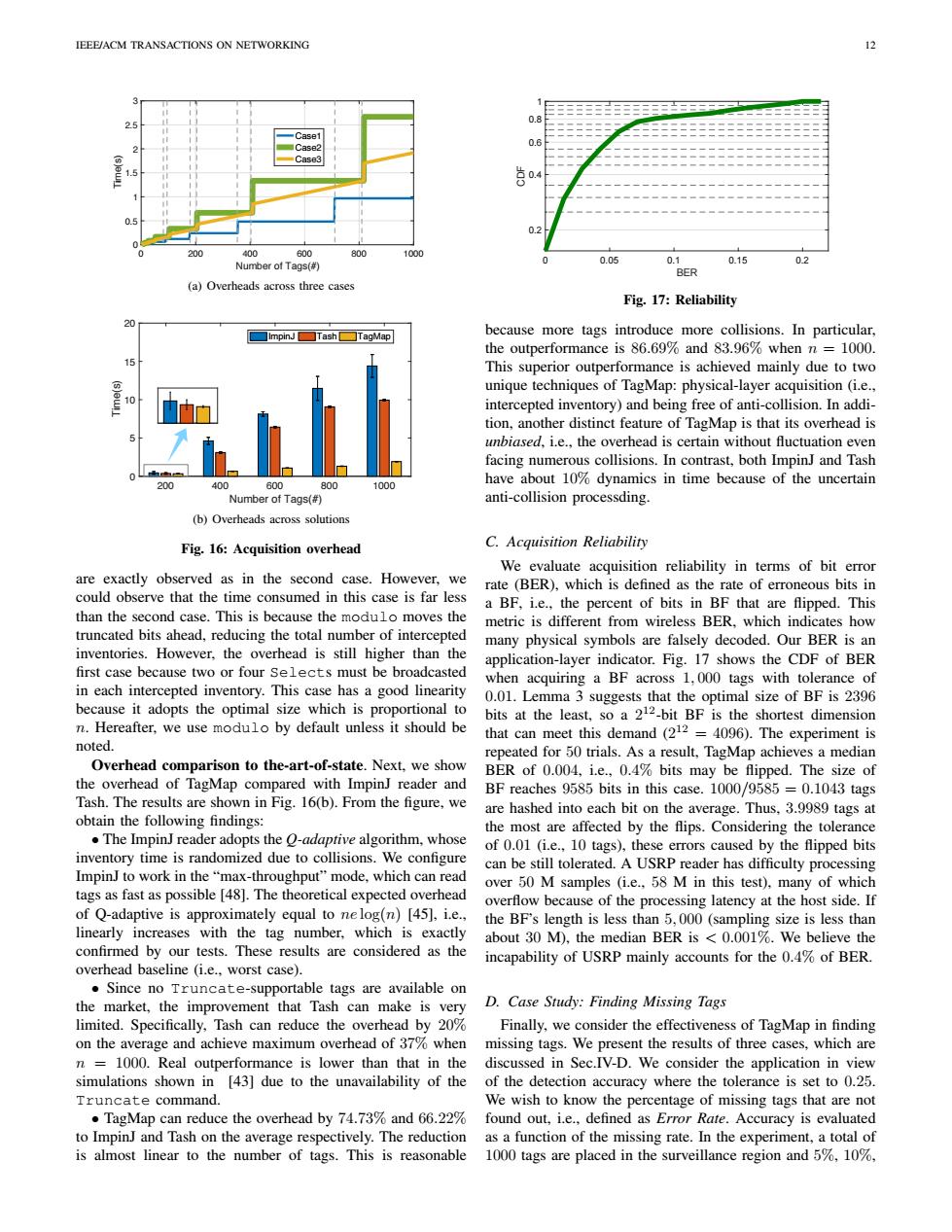
IEEE/ACM TRANSACTIONS ON NETWORKING 12 Case1 0.6 Case Case3 09 200 400 600 800 1000 Number of Tags(#) 0.05 0.1 0.15 02 BER (a)Overheads across three cases Fig.17:Reliability ImpinJ TashTagMap because more tags introduce more collisions.In particular, the outperformance is 86.69%and 83.96%when n=1000 This superior outperformance is achieved mainly due to two unique techniques of TagMap:physical-layer acquisition (i.e., intercepted inventory)and being free of anti-collision.In addi- tion,another distinct feature of TagMap is that its overhead is unbiased,i.e.,the overhead is certain without fluctuation even facing numerous collisions.In contrast,both ImpinJ and Tash 400 600 800 1000 have about 10%dynamics in time because of the uncertain Number of Tags(#) anti-collision processding. (b)Overheads across solutions Fig.16:Acquisition overhead C.Acquisition Reliability We evaluate acquisition reliability in terms of bit error are exactly observed as in the second case.However,we rate (BER),which is defined as the rate of erroneous bits in could observe that the time consumed in this case is far less a BF,i.e.,the percent of bits in BF that are flipped.This than the second case.This is because the modulo moves the metric is different from wireless BER.which indicates how truncated bits ahead,reducing the total number of intercepted many physical symbols are falsely decoded.Our BER is an inventories.However,the overhead is still higher than the application-layer indicator.Fig.17 shows the CDF of BER first case because two or four Selects must be broadcasted when acquiring a BF across 1,000 tags with tolerance of in each intercepted inventory.This case has a good linearity 0.01.Lemma 3 suggests that the optimal size of BF is 2396 because it adopts the optimal size which is proportional to bits at the least,so a 212-bit BF is the shortest dimension n.Hereafter,we use modulo by default unless it should be that can meet this demand(212=4096).The experiment is noted. repeated for 50 trials.As a result,TagMap achieves a median Overhead comparison to the-art-of-state.Next.we show BER of 0.004,i.e.,0.4%bits may be flipped.The size of the overhead of TagMap compared with ImpinJ reader and BF reaches 9585 bits in this case.1000/9585 =0.1043 tags Tash.The results are shown in Fig.16(b).From the figure,we are hashed into each bit on the average.Thus,3.9989 tags at obtain the following findings: the most are affected by the flips.Considering the tolerance .The ImpinJ reader adopts the O-adaptive algorithm,whose of 0.01 (i.e.,10 tags),these errors caused by the flipped bits inventory time is randomized due to collisions.We configure can be still tolerated.A USRP reader has difficulty processing ImpinJ to work in the "max-throughput"mode,which can read over 50 M samples (i.e..58 M in this test).many of which tags as fast as possible [48].The theoretical expected overhead overflow because of the processing latency at the host side.If of Q-adaptive is approximately equal to nelog(n)[45],i.e., the BF's length is less than 5,000(sampling size is less than linearly increases with the tag number,which is exactly about 30 M),the median BER is 0.001%.We believe the confirmed by our tests.These results are considered as the incapability of USRP mainly accounts for the 0.4%of BER. overhead baseline (i.e..worst case). Since no Truncate-supportable tags are available on the market,the improvement that Tash can make is very D.Case Study:Finding Missing Tags limited.Specifically,Tash can reduce the overhead by 20% Finally,we consider the effectiveness of TagMap in finding on the average and achieve maximum overhead of 37%when missing tags.We present the results of three cases,which are n-1000.Real outperformance is lower than that in the discussed in Sec.IV-D.We consider the application in view simulations shown in [43]due to the unavailability of the of the detection accuracy where the tolerance is set to 0.25. Truncate command. We wish to know the percentage of missing tags that are not .TagMap can reduce the overhead by 74.73%and 66.22%found out,i.e.,defined as Error Rate.Accuracy is evaluated to ImpinJ and Tash on the average respectively.The reduction as a function of the missing rate.In the experiment,a total of is almost linear to the number of tags.This is reasonable 1000 tags are placed in the surveillance region and 5%,10%,IEEE/ACM TRANSACTIONS ON NETWORKING 12 0 200 400 600 800 1000 Number of Tags(#) 0 0.5 1 1.5 2 2.5 3 Time(s) Case1 Case2 Case3 (a) Overheads across three cases 200 400 600 800 1000 Number of Tags(#) 0 5 10 15 20 Time(s) ImpinJ Tash TagMap (b) Overheads across solutions Fig. 16: Acquisition overhead are exactly observed as in the second case. However, we could observe that the time consumed in this case is far less than the second case. This is because the modulo moves the truncated bits ahead, reducing the total number of intercepted inventories. However, the overhead is still higher than the first case because two or four Selects must be broadcasted in each intercepted inventory. This case has a good linearity because it adopts the optimal size which is proportional to n. Hereafter, we use modulo by default unless it should be noted. Overhead comparison to the-art-of-state. Next, we show the overhead of TagMap compared with ImpinJ reader and Tash. The results are shown in Fig. 16(b). From the figure, we obtain the following findings: • The ImpinJ reader adopts the Q-adaptive algorithm, whose inventory time is randomized due to collisions. We configure ImpinJ to work in the “max-throughput” mode, which can read tags as fast as possible [48]. The theoretical expected overhead of Q-adaptive is approximately equal to ne log(n) [45], i.e., linearly increases with the tag number, which is exactly confirmed by our tests. These results are considered as the overhead baseline (i.e., worst case). • Since no Truncate-supportable tags are available on the market, the improvement that Tash can make is very limited. Specifically, Tash can reduce the overhead by 20% on the average and achieve maximum overhead of 37% when n = 1000. Real outperformance is lower than that in the simulations shown in [43] due to the unavailability of the Truncate command. • TagMap can reduce the overhead by 74.73% and 66.22% to ImpinJ and Tash on the average respectively. The reduction is almost linear to the number of tags. This is reasonable 0 0.05 0.1 0.15 0.2 BER 0.2 0.4 0.6 0.8 1 CDF Fig. 17: Reliability because more tags introduce more collisions. In particular, the outperformance is 86.69% and 83.96% when n = 1000. This superior outperformance is achieved mainly due to two unique techniques of TagMap: physical-layer acquisition (i.e., intercepted inventory) and being free of anti-collision. In addi￾tion, another distinct feature of TagMap is that its overhead is unbiased, i.e., the overhead is certain without fluctuation even facing numerous collisions. In contrast, both ImpinJ and Tash have about 10% dynamics in time because of the uncertain anti-collision processding. C. Acquisition Reliability We evaluate acquisition reliability in terms of bit error rate (BER), which is defined as the rate of erroneous bits in a BF, i.e., the percent of bits in BF that are flipped. This metric is different from wireless BER, which indicates how many physical symbols are falsely decoded. Our BER is an application-layer indicator. Fig. 17 shows the CDF of BER when acquiring a BF across 1, 000 tags with tolerance of 0.01. Lemma 3 suggests that the optimal size of BF is 2396 bits at the least, so a 2 12-bit BF is the shortest dimension that can meet this demand (2 12 = 4096). The experiment is repeated for 50 trials. As a result, TagMap achieves a median BER of 0.004, i.e., 0.4% bits may be flipped. The size of BF reaches 9585 bits in this case. 1000/9585 = 0.1043 tags are hashed into each bit on the average. Thus, 3.9989 tags at the most are affected by the flips. Considering the tolerance of 0.01 (i.e., 10 tags), these errors caused by the flipped bits can be still tolerated. A USRP reader has difficulty processing over 50 M samples (i.e., 58 M in this test), many of which overflow because of the processing latency at the host side. If the BF’s length is less than 5, 000 (sampling size is less than about 30 M), the median BER is < 0.001%. We believe the incapability of USRP mainly accounts for the 0.4% of BER. D. Case Study: Finding Missing Tags Finally, we consider the effectiveness of TagMap in finding missing tags. We present the results of three cases, which are discussed in Sec.IV-D. We consider the application in view of the detection accuracy where the tolerance is set to 0.25. We wish to know the percentage of missing tags that are not found out, i.e., defined as Error Rate. Accuracy is evaluated as a function of the missing rate. In the experiment, a total of 1000 tags are placed in the surveillance region and 5%, 10%