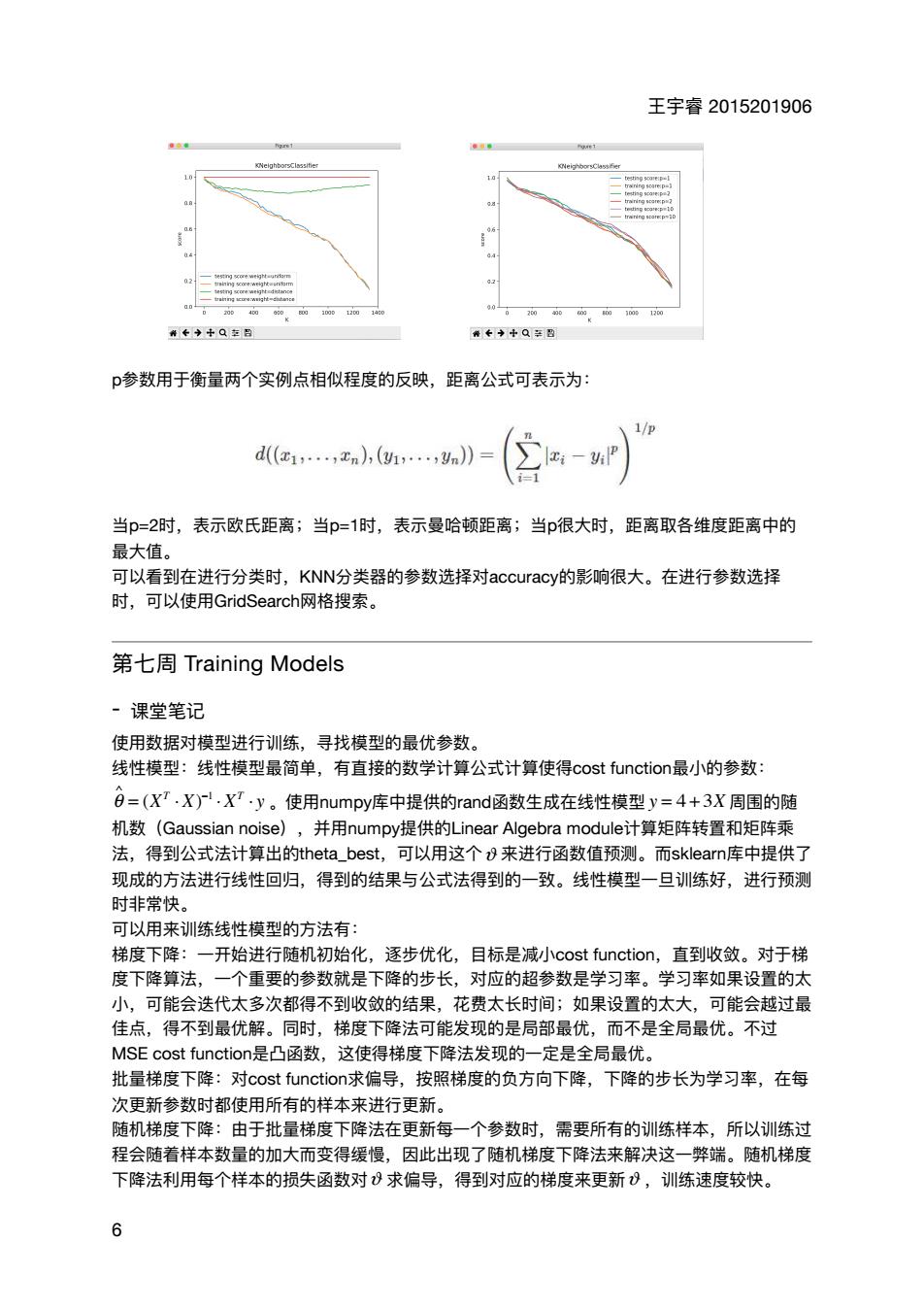
王宇睿2015201906 0←◆+Q包吕 0+++Q多盟 p参数用于衡量两个实例点相似程度的反映，距离公式可表示为： 1/0 d(1,,xn,(…,y》= ∑-P】 当p=2时，表示欧氏距离；当p=1时，表示曼哈顿距离；当p很大时，距离取各维度距离中的 最大值。 可以看到在进行分类时，KNN分类器的参数选择对accuracy的影响很大。在进行参数选择 时，可以使用GridSearch网格搜索。 第七周Training Models ·课堂笔记 使用数据对模型进行训练，寻找模型的最优参数。 线性模型：线性模型最简单，有直接的数学计算公式计算使得cost function最小的参数： 日=(XT,X).XT·y。使用numpy库中提供的rand函数生成在线性模型y=4+3X周围的随 机数(Gaussian noise) ,并用numpy提供的Linear Algebra module计算矩阵转置和矩阵乘 法，得到公式法计算出的theta_best,可以用这个&来进行函数值预测。而sklearn库中提供了 现成的方法进行线性回归，得到的结果与公式法得到的一致。线性模型一旦训练好，进行预测 时非常快。 可以用来训练线性模型的方法有： 梯度下降：一开始进行随机初始化，逐步优化，目标是减小cost function,直到收敛。对于梯 度下降算法，一个重要的参数就是下降的步长，对应的超参数是学习率。学习率如果设置的太 小，可能会迭代太多次都得不到收敛的结果，花费太长时间；如果设置的太大 ,可能会越过最 佳点，得不到最优解。同时，梯度下降法可能发现的是局部最优，而不是全局最优。不过 MSE cost function是凸函数，这使得梯度下降法发现的一定是全局最优。 批量梯度下降：对cost function求偏导，按照梯度的负方向下降，下降的步长为学习率，在每 次更新参数时都使用所有的样本来进行更新 随机梯度下降：由于批量梯度下降法在更新每一个参数时，需要所有的训练样本，所以训练过 程会随着样本数量的加大而变得缓慢，因此出现了随机梯度下降法来解决这一弊端。随机梯度 下降法利用每个样本的损失函数对8求偏导，得到对应的梯度来更新8，训练速度较快。王宇睿 2015201906 p参数⽤于衡量两个实例点相似程度的反映，距离公式可表示为： 当p=2时，表示欧⽒距离；当p=1时，表示曼哈顿距离；当p很⼤时，距离取各维度距离中的 最⼤值。 可以看到在进⾏分类时，KNN分类器的参数选择对accuracy的影响很⼤。在进⾏参数选择 时，可以使⽤GridSearch⽹格搜索。 第七周 Training Models - 课堂笔记 使⽤数据对模型进⾏训练，寻找模型的最优参数。 线性模型：线性模型最简单，有直接的数学计算公式计算使得cost function最⼩的参数： 。使⽤numpy库中提供的rand函数⽣成在线性模型 周围的随 机数（Gaussian noise），并⽤numpy提供的Linear Algebra module计算矩阵转置和矩阵乘 法，得到公式法计算出的theta_best，可以⽤这个 来进⾏函数值预测。⽽sklearn库中提供了 现成的⽅法进⾏线性回归，得到的结果与公式法得到的⼀致。线性模型⼀旦训练好，进⾏预测 时⾮常快。 可以⽤来训练线性模型的⽅法有： 梯度下降：⼀开始进⾏随机初始化，逐步优化，⽬标是减⼩cost function，直到收敛。对于梯 度下降算法，⼀个᯿要的参数就是下降的步⻓，对应的超参数是学习率。学习率如果设置的太 ⼩，可能会迭代太多次都得不到收敛的结果，花费太⻓时间；如果设置的太⼤，可能会越过最 佳点，得不到最优解。同时，梯度下降法可能发现的是局部最优，⽽不是全局最优。不过 MSE cost function是凸函数，这使得梯度下降法发现的⼀定是全局最优。 批量梯度下降：对cost function求偏导，按照梯度的负⽅向下降，下降的步⻓为学习率，在每 次更新参数时都使⽤所有的样本来进⾏更新。 随机梯度下降：由于批量梯度下降法在更新每⼀个参数时，需要所有的训练样本，所以训练过 程会随着样本数量的加⼤⽽变得缓慢，因此出现了随机梯度下降法来解决这⼀弊端。随机梯度 下降法利⽤每个样本的损失函数对 求偏导，得到对应的梯度来更新 ，训练速度较快。 θ ∧ = (XT ⋅ X) −1 ⋅ XT ⋅ y y = 4 + 3X ϑ ϑ ϑ 6