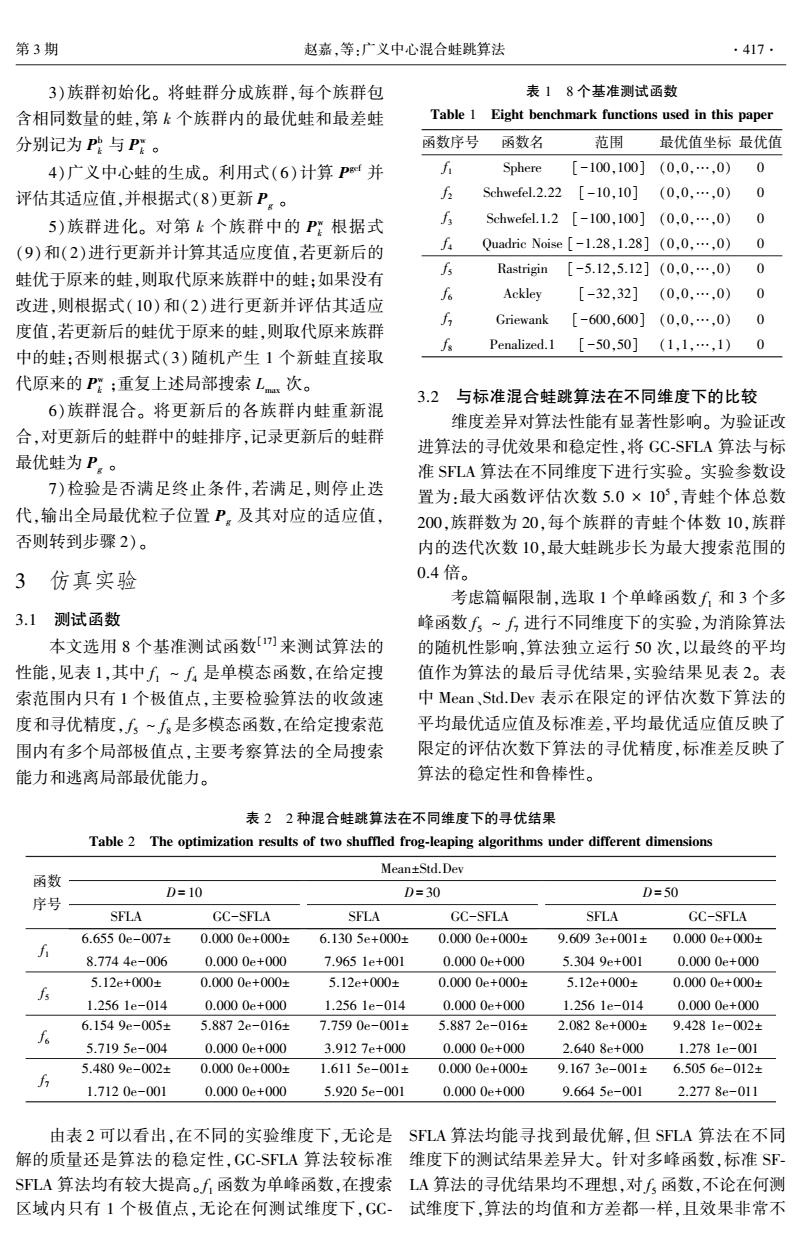
第3期 赵嘉，等：广义中心混合蛙跳算法 ·417- 3)族群初始化。将蛙群分成族群，每个族群包 表18个基准测试函数 含相同数量的蛙，第k个族群内的最优蛙和最差蛙 Table 1 Eight benchmark functions used in this paper 分别记为P与Pg。 函数序号 函数名 范围 最优值坐标最优值 4)广义中心蛙的生成。利用式(6)计算P时并 Sphere [-100.100](0.0.…,0) 0 评估其适应值，并根据式(8)更新P。。 1 Schwefel.2.22 [-10,10] (0,0,…,0) 0 5)族群进化。对第k个族群中的P:根据式 f Schwefel.1.2[-100,100](0,0,…,0) 0 (9)和(2)进行更新并计算其适应度值，若更新后的 Quadric Noise[-1.28,1.28](0,0,…,0) 0 5 Rastrigin [-5.12,5.12](0,0,…,0) 蛙优于原来的蛙，则取代原来族群中的蛙：如果没有 0 Ackley [-32,32](0,0,…,0) 0 改进，则根据式(10)和(2)进行更新并评估其适应 Griewank [-600,600](0,0,…,0) 0 度值，若更新后的蛙优于原来的蛙，则取代原来族群 Penalized..1[-50,50](1,l,…,1)0 中的蛙：否则根据式(3)随机产生1个新蛙直接取 代原来的P:重复上述局部搜索L次。 3.2与标准混合蛙跳算法在不同维度下的比较 6)族群混合。将更新后的各族群内蛙重新混 维度差异对算法性能有显著性影响。为验证改 合，对更新后的蛙群中的蛙排序，记录更新后的蛙群 进算法的寻优效果和稳定性，将GC-SFLA算法与标 最优蛙为P。。 准SFLA算法在不同维度下进行实验。实验参数设 7)检验是否满足终止条件，若满足，则停止迭 置为：最大函数评估次数5.0×10，青蛙个体总数 代，输出全局最优粒子位置P。及其对应的适应值， 200,族群数为20，每个族群的青蛙个体数10，族群 否则转到步骤2)。 内的迭代次数10，最大蛙跳步长为最大搜索范围的 3 仿真实验 0.4倍。 考虑篇幅限制，选取1个单峰函数∫和3个多 3.1测试函数 峰函数∫~，进行不同维度下的实验，为消除算法 本文选用8个基准测试函数[)来测试算法的 的随机性影响，算法独立运行50次，以最终的平均 性能，见表1，其中f~f是单模态函数，在给定搜 值作为算法的最后寻优结果，实验结果见表2。表 索范围内只有1个极值点，主要检验算法的收敛速 中Mean、Std.Dev表示在限定的评估次数下算法的 度和寻优精度，了~∫是多模态函数，在给定搜索范 平均最优适应值及标准差，平均最优适应值反映了 围内有多个局部极值点，主要考察算法的全局搜索 限定的评估次数下算法的寻优精度，标准差反映了 能力和逃离局部最优能力。 算法的稳定性和鲁棒性。 表22种混合蛙跳算法在不同维度下的寻优结果 Table 2 The optimization results of two shuffled frog-leaping algorithms under different dimensions Mean±Std.Dev 函数 D=10 D=30 D=50 序号 SFLA GC-SFLA SFLA GC-SFLA SFLA GC-SFLA 6.6550e-007± 0.0000e+000± 6.1305e+000± 0.0000e+000± 9.6093e+001±0.0000e+000± f月 8.7744e-006 0.0000e+000 7.9651e+001 0.0000e+000 5.3049e+001 0.0000e+000 5.12e+000± 0.0000e+000± 5.12e+000± 0.0000e+000± 5.12e+000± 0.0000e+000± 1.2561e-014 0.0000e+000 1.2561e-014 0.0000e+000 1.2561e-014 0.0000e+000 6.1549e-005± 5.8872e-016± 7.7590e-001± 5.8872e-016± 2.0828e+000± 9.4281e-002± 5.7195e-004 0.0000e+000 3.9127e+000 0.0000e+000 2.6408e+000 1.2781e-001 5.4809e-002± 0.0000e+000± 1.6115e-001± 0.0000e+000± 9.1673e-001± 6.5056e-012± f 1.7120e-001 0.0000e+000 5.9205e-001 0.0000e+000 9.6645e-001 2.2778e-011 由表2可以看出，在不同的实验维度下，无论是SLA算法均能寻找到最优解，但SLA算法在不同 解的质量还是算法的稳定性，GC-SLA算法较标准维度下的测试结果差异大。针对多峰函数，标准SF SFLA算法均有较大提高。f1函数为单峰函数，在搜索LA算法的寻优结果均不理想，对f5函数，不论在何测 区域内只有1个极值点，无论在何测试维度下，GC-试维度下，算法的均值和方差都一样，且效果非常不３）族群初始化。 将蛙群分成族群，每个族群包 含相同数量的蛙，第 ｋ 个族群内的最优蛙和最差蛙 分别记为 Ｐ ｂ ｋ 与 Ｐ ｗ ｋ 。 ４）广义中心蛙的生成。 利用式（６）计算 Ｐ ｇｃｆ 并 评估其适应值，并根据式（８）更新 Ｐｇ 。 ５）族群进化。 对第 ｋ 个族群中的 Ｐ ｗ ｋ 根据式 （９）和（２）进行更新并计算其适应度值，若更新后的 蛙优于原来的蛙，则取代原来族群中的蛙；如果没有 改进，则根据式（１０）和（２）进行更新并评估其适应 度值，若更新后的蛙优于原来的蛙，则取代原来族群 中的蛙；否则根据式（３）随机产生 １ 个新蛙直接取 代原来的 Ｐ ｗ ｋ ；重复上述局部搜索 Ｌｍａｘ 次。 ６）族群混合。 将更新后的各族群内蛙重新混 合，对更新后的蛙群中的蛙排序，记录更新后的蛙群 最优蛙为 Ｐｇ 。 ７）检验是否满足终止条件，若满足，则停止迭 代，输出全局最优粒子位置 Ｐｇ 及其对应的适应值， 否则转到步骤 ２）。 ３ 仿真实验 ３．１ 测试函数 本文选用 ８ 个基准测试函数［１７］ 来测试算法的 性能，见表 １，其中 ｆ １ ～ ｆ ４ 是单模态函数，在给定搜 索范围内只有 １ 个极值点，主要检验算法的收敛速 度和寻优精度， ｆ ５ ～ ｆ ８ 是多模态函数，在给定搜索范 围内有多个局部极值点，主要考察算法的全局搜索 能力和逃离局部最优能力。 表 １ ８ 个基准测试函数 Ｔａｂｌｅ １ Ｅｉｇｈｔ ｂｅｎｃｈｍａｒｋ ｆｕｎｃｔｉｏｎｓ ｕｓｅｄ ｉｎ ｔｈｉｓ ｐａｐｅｒ 函数序号 函数名 范围 最优值坐标 最优值 ｆ １ Ｓｐｈｅｒｅ ［－１００，１００］ （０，０，…，０） ０ ｆ ２ Ｓｃｈｗｅｆｅｌ．２．２２ ［－１０，１０］ （０，０，…，０） ０ ｆ ３ Ｓｃｈｗｅｆｅｌ．１．２ ［－１００，１００］ （０，０，…，０） ０ ｆ ４ Ｑｕａｄｒｉｃ Ｎｏｉｓｅ ［－１．２８，１．２８］ （０，０，…，０） ０ ｆ ５ Ｒａｓｔｒｉｇｉｎ ［－５．１２，５．１２］ （０，０，…，０） ０ ｆ ６ Ａｃｋｌｅｙ ［－３２，３２］ （０，０，…，０） ０ ｆ ７ Ｇｒｉｅｗａｎｋ ［－６００，６００］ （０，０，…，０） ０ ｆ ８ Ｐｅｎａｌｉｚｅｄ．１ ［－５０，５０］ （１，１，…，１） ０ ３．２ 与标准混合蛙跳算法在不同维度下的比较 维度差异对算法性能有显著性影响。 为验证改 进算法的寻优效果和稳定性，将 ＧＣ⁃ＳＦＬＡ 算法与标 准 ＳＦＬＡ 算法在不同维度下进行实验。 实验参数设 置为：最大函数评估次数 ５．０ × １０ ５ ，青蛙个体总数 ２００，族群数为 ２０，每个族群的青蛙个体数 １０，族群 内的迭代次数 １０，最大蛙跳步长为最大搜索范围的 ０．４ 倍。 考虑篇幅限制，选取 １ 个单峰函数 ｆ １ 和 ３ 个多 峰函数 ｆ ５ ～ ｆ ７ 进行不同维度下的实验，为消除算法 的随机性影响，算法独立运行 ５０ 次，以最终的平均 值作为算法的最后寻优结果，实验结果见表 ２。 表 中 Ｍｅａｎ、Ｓｔｄ．Ｄｅｖ 表示在限定的评估次数下算法的 平均最优适应值及标准差，平均最优适应值反映了 限定的评估次数下算法的寻优精度，标准差反映了 算法的稳定性和鲁棒性。 表 ２ ２ 种混合蛙跳算法在不同维度下的寻优结果 Ｔａｂｌｅ ２ Ｔｈｅ ｏｐｔｉｍｉｚａｔｉｏｎ ｒｅｓｕｌｔｓ ｏｆ ｔｗｏ ｓｈｕｆｆｌｅｄ ｆｒｏｇ⁃ｌｅａｐｉｎｇ ａｌｇｏｒｉｔｈｍｓ ｕｎｄｅｒ ｄｉｆｆｅｒｅｎｔ ｄｉｍｅｎｓｉｏｎｓ 函数 序号 Ｍｅａｎ±Ｓｔｄ．Ｄｅｖ Ｄ＝ １０ ＳＦＬＡ ＧＣ－ＳＦＬＡ Ｄ＝ ３０ ＳＦＬＡ ＧＣ－ＳＦＬＡ Ｄ＝ ５０ ＳＦＬＡ ＧＣ－ＳＦＬＡ ｆ １ ６．６５５ ０ｅ－００７± ８．７７４ ４ｅ－００６ ０．０００ ０ｅ＋０００± ０．０００ ０ｅ＋０００ ６．１３０ ５ｅ＋０００± ７．９６５ １ｅ＋００１ ０．０００ ０ｅ＋０００± ０．０００ ０ｅ＋０００ ９．６０９ ３ｅ＋００１± ５．３０４ ９ｅ＋００１ ０．０００ ０ｅ＋０００± ０．０００ ０ｅ＋０００ ｆ ５ ５．１２ｅ＋０００± １．２５６ １ｅ－０１４ ０．０００ ０ｅ＋０００± ０．０００ ０ｅ＋０００ ５．１２ｅ＋０００± １．２５６ １ｅ－０１４ ０．０００ ０ｅ＋０００± ０．０００ ０ｅ＋０００ ５．１２ｅ＋０００± １．２５６ １ｅ－０１４ ０．０００ ０ｅ＋０００± ０．０００ ０ｅ＋０００ ｆ ６ ６．１５４ ９ｅ－００５± ５．７１９ ５ｅ－００４ ５．８８７ ２ｅ－０１６± ０．０００ ０ｅ＋０００ ７．７５９ ０ｅ－００１± ３．９１２ ７ｅ＋０００ ５．８８７ ２ｅ－０１６± ０．０００ ０ｅ＋０００ ２．０８２ ８ｅ＋０００± ２．６４０ ８ｅ＋０００ ９．４２８ １ｅ－００２± １．２７８ １ｅ－００１ ｆ ７ ５．４８０ ９ｅ－００２± １．７１２ ０ｅ－００１ ０．０００ ０ｅ＋０００± ０．０００ ０ｅ＋０００ １．６１１ ５ｅ－００１± ５．９２０ ５ｅ－００１ ０．０００ ０ｅ＋０００± ０．０００ ０ｅ＋０００ ９．１６７ ３ｅ－００１± ９．６６４ ５ｅ－００１ ６．５０５ ６ｅ－０１２± ２．２７７ ８ｅ－０１１ 由表 ２ 可以看出，在不同的实验维度下，无论是 解的质量还是算法的稳定性，ＧＣ⁃ＳＦＬＡ 算法较标准 ＳＦＬＡ 算法均有较大提高。 ｆ １ 函数为单峰函数，在搜索 区域内只有 １ 个极值点，无论在何测试维度下，ＧＣ⁃ ＳＦＬＡ 算法均能寻找到最优解，但 ＳＦＬＡ 算法在不同 维度下的测试结果差异大。 针对多峰函数，标准 ＳＦ⁃ ＬＡ 算法的寻优结果均不理想，对 ｆ ５ 函数，不论在何测 试维度下，算法的均值和方差都一样，且效果非常不 第 ３ 期 赵嘉，等：广义中心混合蛙跳算法 ·４１７·