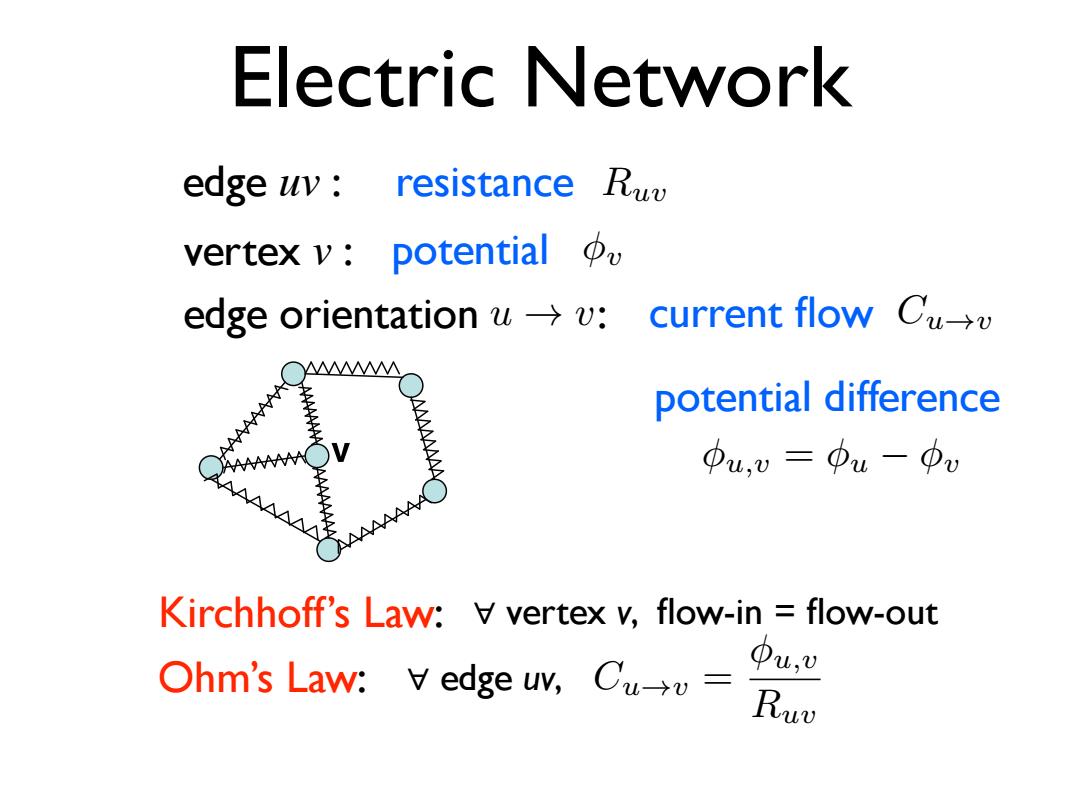
Electric Network edge uv:resistance Ruv vertex v:potential edge orientation u→w: current flow Cu-→v potential difference Pu,v Pu-pv Kirchhoff's Law:V vertex v,flow-in flow-out Ohm's Law:V edge uv,Cu= ①u, Ruv23-2 Lecture 23: November 17 Notes 1. The above two algorithms demonstrate a time-space tradeo↵, in that the product of space and time remains constant. In fact, it turns out that there is a whole spectrum of randomized algorithms spanning this tradeo↵ [F97]: 8s 9 algorithm using space s and time O˜(|V ||E| s ) that visits all (reachable) vertices w.h.p. (The notation O˜ hides logarithmic as well as constant factors.) 2. In an important breakthrough, Reingold [R05] showed that the above random walk algorithm could be derandomized, thus obtaining a deterministic O(1) space algorithm for graph searching (phrased more precisely as testing whether there is a path between a given pair of vertices u, v. More correctly this is a O(log n) space algorithm, since O(log n) space is needed to record the label of a vertex in an n-vertex graph, and to keep track of the number of steps taken so far.) Since the connectivity problem is a canonical problem solvable in randomized log-space, this seems like a major step towards proving that every randomized log-space algorithm can be derandomized with only a constant factor penalty in space. However, this question remains open (see, e.g., [RTV06] for some interesting approaches). We should also observe that the analogous question for directed graphs is much more challenging, since testing connectivity in this case is a complete problem for non-deterministic log-space. Thus a deterministic (or even randomized) log-space algorithm for it would show that even non-determinism buys us nothing in the world of log-space algorithms. One problem here is that the naive random walk approach breaks down because the cover time on directed graphs can be exponentially large. The bound on the cover time comes from the following theorem, originally due to Aleliunas et al. [AKLLR79]. Theorem 23.4 For any connected graph G, C(G)  2|E||V |. We will follow a di↵erent route due to Chandra et al. [CRRST89], which is based on an intriguing connection between random walks and electrical networks. Along the way, we will also obtain bounds on hitting times. 23.2 Hitting time and commute time To prove theorem 23.4, we start by proving some properties of the hitting time for a vertex. To do this, we will view the graph as an electrical network, where each edge has unit resistance. (For a detailed treatment of the relationship between random walks and electrical networks, see the classic book by Doyle and Snell [DS84].) When a potential di↵erence is applied between nodes of this network from an external source, current flows in the network in accordance with Kircho↵’s Laws and Ohm’s Laws: • K1: The total current into and out of a vertex is equal to zero. • K2: The sum of potential di↵erences around any cycle is zero. • Ohm’s Law: The current flowing along any edge is equal to pot. di↵erence resistance . Electric Network edge uv : resistance Ruv vertex v : potential ￾v edge orientation u ! v: current flow Cu!v Kirchhoff’s Law: ∀ vertex v, flow-in = flow-out Ohm’s Law: ∀ edge uv, Cu!v = ￾u,v Ruv potential difference ￾u,v = ￾u ￾ ￾v