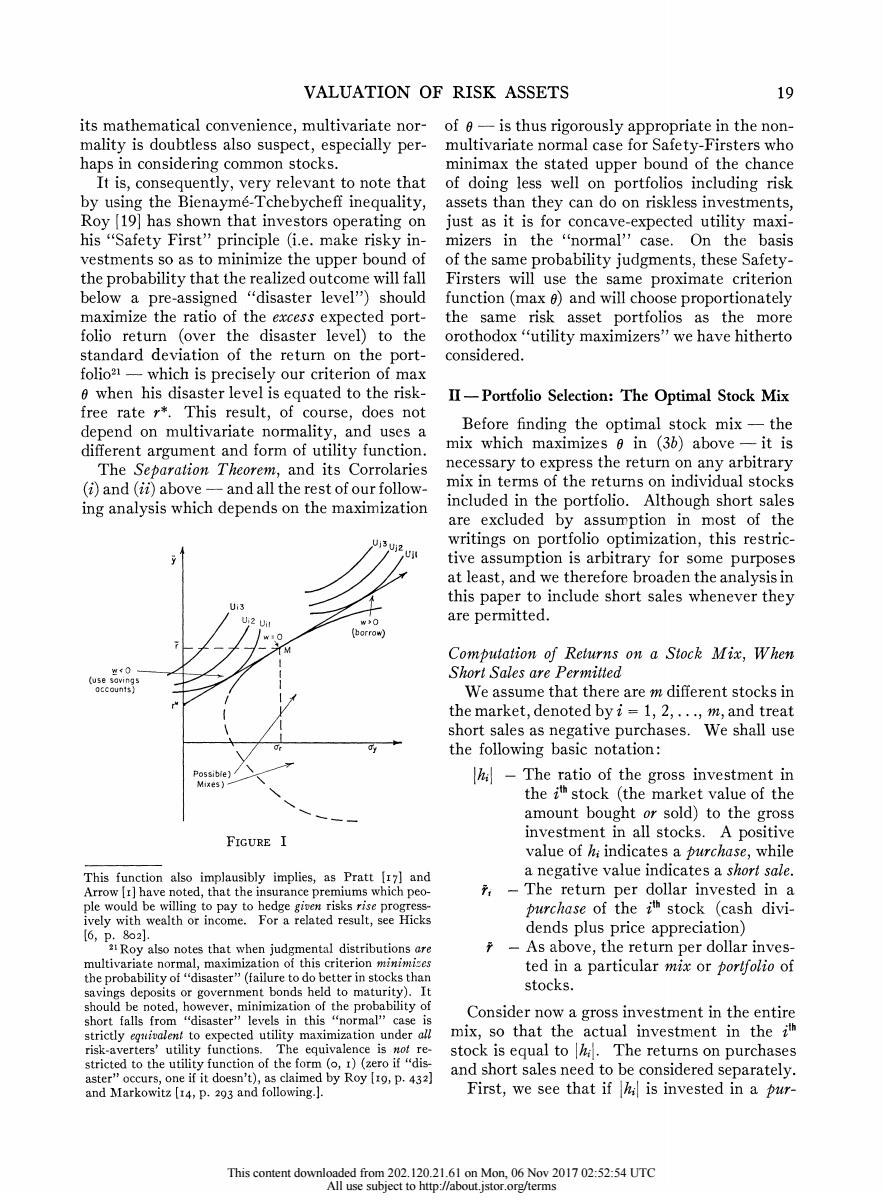
VALUATION OF RISK ASSETS 19 its mathematical convenience,multivariate nor-of-is thus rigorously appropriate in the non- mality is doubtless also suspect,especially per-multivariate normal case for Safety-Firsters who haps in considering common stocks. minimax the stated upper bound of the chance It is,consequently,very relevant to note that of doing less well on portfolios including risk by using the Bienayme-Tchebycheff inequality,assets than they can do on riskless investments, Roy [19]has shown that investors operating on just as it is for concave-expected utility maxi- his "Safety First"'principle (i.e.make risky in-mizers in the "normal''case.On the basis vestments so as to minimize the upper bound of of the same probability judgments,these Safety- the probability that the realized outcome will fall Firsters will use the same proximate criterion below a pre-assigned "disaster level")should function(max )and will choose proportionately maximize the ratio of the excess expected port-the same risk asset portfolios as the more folio return (over the disaster level)to the orothodox"utility maximizers"we have hitherto standard deviation of the return on the port-considered. folio2-which is precisely our criterion of max 0 when his disaster level is equated to the risk-II-Portfolio Selection:The Optimal Stock Mix free rate r*.This result,of course,does not depend on multivariate normality,and uses a Before finding the optimal stock mix-the different argument and form of utility function. mix which maximizes 0 in (36)above-it is The Separation Theorem,and its Corrolaries necessary to express the return on any arbitrary (i)and (ii)above-and all the rest of our follow- mix in terms of the returns on individual stocks ing analysis which depends on the maximization included in the portfolio.Although short sales are excluded by assumption in most of the writings on portfolio optimization,this restric- tive assumption is arbitrary for some purposes at least,and we therefore broaden the analysis in this paper to include short sales whenever they Ui3 Ui2 Uil w事O are permitted. (化orrow) Computation of Returns on a Stock Mix,When (use r0 Short Sales are Permitted We assume that there are m different stocks in the market,denoted by i=1,2,...,m,and treat short sales as negative purchases.We shall use the following basic notation: Possiblel -The ratio of the gross investment in the ith stock (the market value of the amount bought or sold)to the gross FIGURE I investment in all stocks.A positive value of hi indicates a purchase,while This function also implausibly implies,as Pratt [I7]and a negative value indicates a short sale. Arrow [r]have noted,that the insurance premiums which peo- -The return per dollar invested in a ple would be willing to pay to hedge gioen risks rise progress- purchase of the ith stock (cash divi- ively with wealth or income.For a related result,see Hicks I6,P.8o2l. dends plus price appreciation) a Roy also notes that when judgmental distributions are -As above,the return per dollar inves- multivariate normal,maximization of this criterion minimises ted in a particular mix or porlfolio of the probability of "disaster"(failure to do better in stocks than savings deposits or government bonds held to maturity).It stocks. should be noted,however,minimization of the probability of short falls from "disaster"levels in this "normal''case is Consider now a gross investment in the entire strictly eguivalent to expected utility maximization under all mix,so that the actual investment in the i risk-averters'utility functions.The equivalence is not re- stock is equal to The returns on purchases stricted to the utility function of the form (o,I)(zero if "dis- aster"occurs,one if it doesn't),as claimed by Roy [1o,p.432) and short sales need to be considered separately. and Markowitz [14,p.293 and following.]. First,we see that if is invested in a pur- This content downloaded from 202.120.21.61 on Mon,06 Nov 2017 02:52:54 UTC All use subject to http://about.jstor.org/termsVALUATION OF RISK ASSETS 19 its mathematical convenience, multivariate nor- mality is doubtless also suspect, especially per- haps in considering common stocks. It is, consequently, very relevant to note that by using the Bienayme-Tchebycheff inequality, Roy [19] has shown that investors operating on his "Safety First" principle (i.e. make risky in- vestments so as to minimize the upper bound of the probability that the realized outcome will fall below a pre-assigned "disaster level") should maximize the ratio of the excess expected port- folio return (over the disaster level) to the standard deviation of the return on the port- folio2l - which is precisely our criterion of max 0 when his disaster level is equated to the risk- free rate r*. This result, of course, does not depend on multivariate normality, and uses a different argument and form of utility function. The Separation Theorem, and its Corrolaries (i) and (ii) above - and all the rest of our follow- ing analysis which depends on the maximization Uj3 Uj2 U1" Ui3 Ui2 U w>O o /27< (borrow) w < 0 (use savings accounts) / Possible) Mixes) FIGURE I of 0 - is thus rigorously appropriate in the non- multivariate normal case for Safety-Firsters who minimax the stated upper bound of the chance of doing less well on portfolios including risk assets than they can do on riskless investments, just as it is for concave-expected utility maxi- mizers in the "normal" case. On the basis of the same probability judgments, these Safety- Firsters will use the same proximate criterion function (max o) and will choose proportionately the same risk asset portfolios as the more orothodox "utility maximizers" we have hitherto considered. II -Portfolio Selection: The Optimal Stock Mix Before finding the optimal stock mix - the mix which maximizes 0 in (3b) above -it is necessary to express the return on any arbitrary mix in terms of the returns on individual stocks included in the portfolio. Although short sales are excluded by assumption in most of the writings on portfolio optimization, this restric- tive assumption is arbitrary for some purposes at least, and we therefore broaden the analysis in this paper to include short sales whenever they are permitted. Computation of Returns on a Stock Mix, When Short Sales are Permitted We assume that there are m different stocks in the market, denoted by i = 1, 2, .. ., m, and treat short sales as negative purchases. We shall use the following basic notation: -hil The ratio of the gross investment in the Pth stock (the market value of the amount bought or sold) to the gross investment in all stocks. A positive value of hi indicates a purchase, while a negative value indicates a short sale. - The return per dollar invested in a purchase of the Pth stock (cash divi- dends plus price appreciation) - As above, the return per dollar inves- ted in a particular mix or portfolio of stocks. Consider now a gross investment in the entire mix, so that the actual investment in the ith stock is equal to Ihil. The returns on purchases and short sales need to be considered separately. First, we see that if 1hil is invested in a pur- This function also implausibly implies, as Pratt |I 7] and Arrow [i] have noted, that the insurance premiums which peo- ple would be willing to pay to hedge given risks rise progress- ively with wealth or income. For a related result, see Hicks [6, p. 802]. 2'Roy also notes that when judgmental distributions are multivariate normal, maximization of this criterion minimizes the probability of "disaster" (failure to do better in stocks than savings deposits or government bonds held to maturity). It should be noted, however, minimization of the probability of short falls from "disaster" levels in this "normal" case is strictly eqiuivalent to expected utility maximization under all risk-averters' utility functions. The equivalence is not re- stricted to the utility function of the form (o, i) (zero if "dis- aster" occurs, one if it doesn't), as claimed by Roy [I9, P. 432] and Markowitz [I4, P. 293 and following.]. This content downloaded from 202.120.21.61 on Mon, 06 Nov 2017 02:52:54 UTC All use subject to http://about.jstor.org/terms