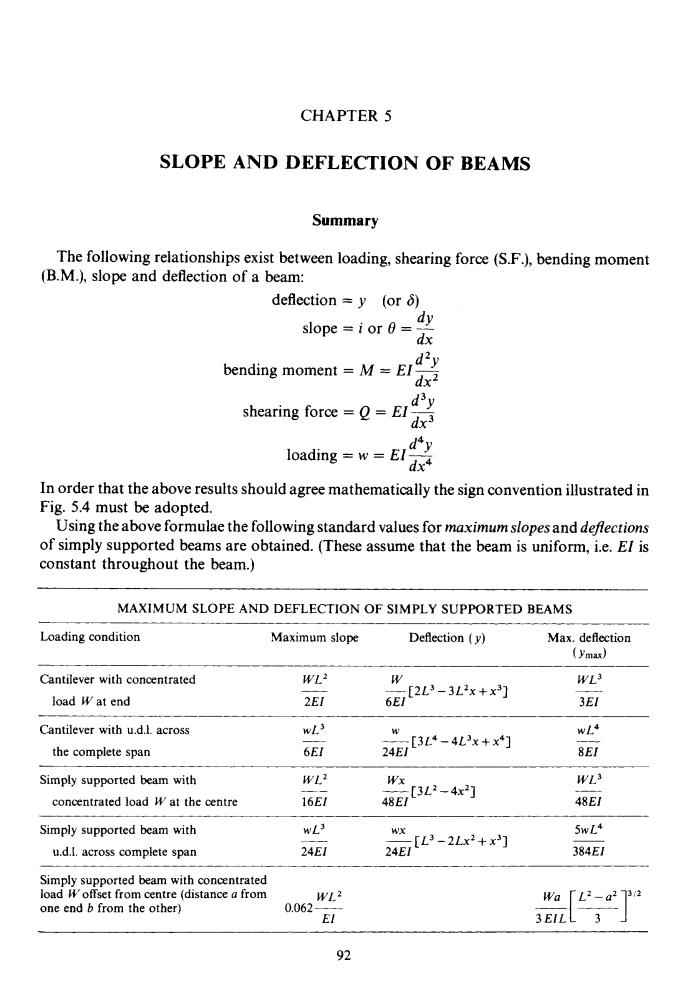
CHAPTER 5 SLOPE AND DEFLECTION OF BEAMS Summary The following relationships exist between loading,shearing force(S.F.),bending moment (B.M.),slope and deflection of a beam: deflection =y (or 6) slope i or 0= dy dx bending moment M=EI d2y 2 shearing forceE dx3 loading =w=EI dxi In order that the above results should agree mathematically the sign convention illustrated in Fig.5.4 must be adopted. Using the above formulae the following standard values for maximum slopes and deftections of simply supported beams are obtained.(These assume that the beam is uniform,i.e.El is constant throughout the beam.) MAXIMUM SLOPE AND DEFLECTION OF SIMPLY SUPPORTED BEAMS Loading condition Maximum slope Deflection (y) Max.deflection (ymax)） Cantilever with concentrated WL2 W WL3 load W at end 2E1 i[2L-3Lx 3El Cantilever with u.d.l.across wL3 the complete span 6EI 24E3L4-4Lx+x的 wL4 8EI Simply supported beam with WL2 Wx WL> concentrated load W at the centre 16E1 48ei3L2-4] 48E1 Simply supported beam with wL3 WX 5wL4 u.d.I.across complete span 24E1 24E[L-2x+ 384E1 Simply supported beam with concentrated load W offset from centre (distance a from WL2 Wa one end b from the other) 0.062 El 92CHAPTER 5 SLOPE AND DEFLECTION OF BEAMS Summary The following relationships exist between loading, shearing force (S.F.), bending moment (B.M.), slope and deflection of a beam: deflection = y (or 6) dY slope = i or 0 = - dx d2Y bending moment = M = EI ~ dx2 d3Y shearing force = Q = EI￾dx3 d4Y loading = w = EI- dx4 In order that the above results should agree mathematically the sign convention illustrated in Fig. 5.4 must be adopted. Using the above formulae the following standard values for maximum slopes and dejections of simply supported beams are obtained. (These assume that the beam is uniform, i.e. EI is constant throughout the beam.) MAXIMUM SLOPE AND DEFLECTION OF SIMPLY SUPPORTED BEAMS Loading condition Maximum slope Deflection ( y) Max. deflection (YId Cantilever with concentrated load Wat end WL2 2EI W 6E1 - ~2~3 - 3 ~2~ + x3~ WL3 3EI Cantilever with u.d.1. across the complete span wL3 6EI - W __ [3L4 - 4L3x + x4] 24EI wL4 8EI ~ Simply supported beam with concentrated load W at the centre WLZ 16EI wx 48EI __ [3L2 - 4x23 WL3 48EI ~ Simply supported beam with u.d.1. across complete span wL3 24EI ~ wx ~ [ L3 - 2Lx2 + x3] 24EI 5wL4 384EI ~ Simply supported beam with concentrated load W offset from centre (distance a from WLZ 0.062 __ El one end b from the other) 92