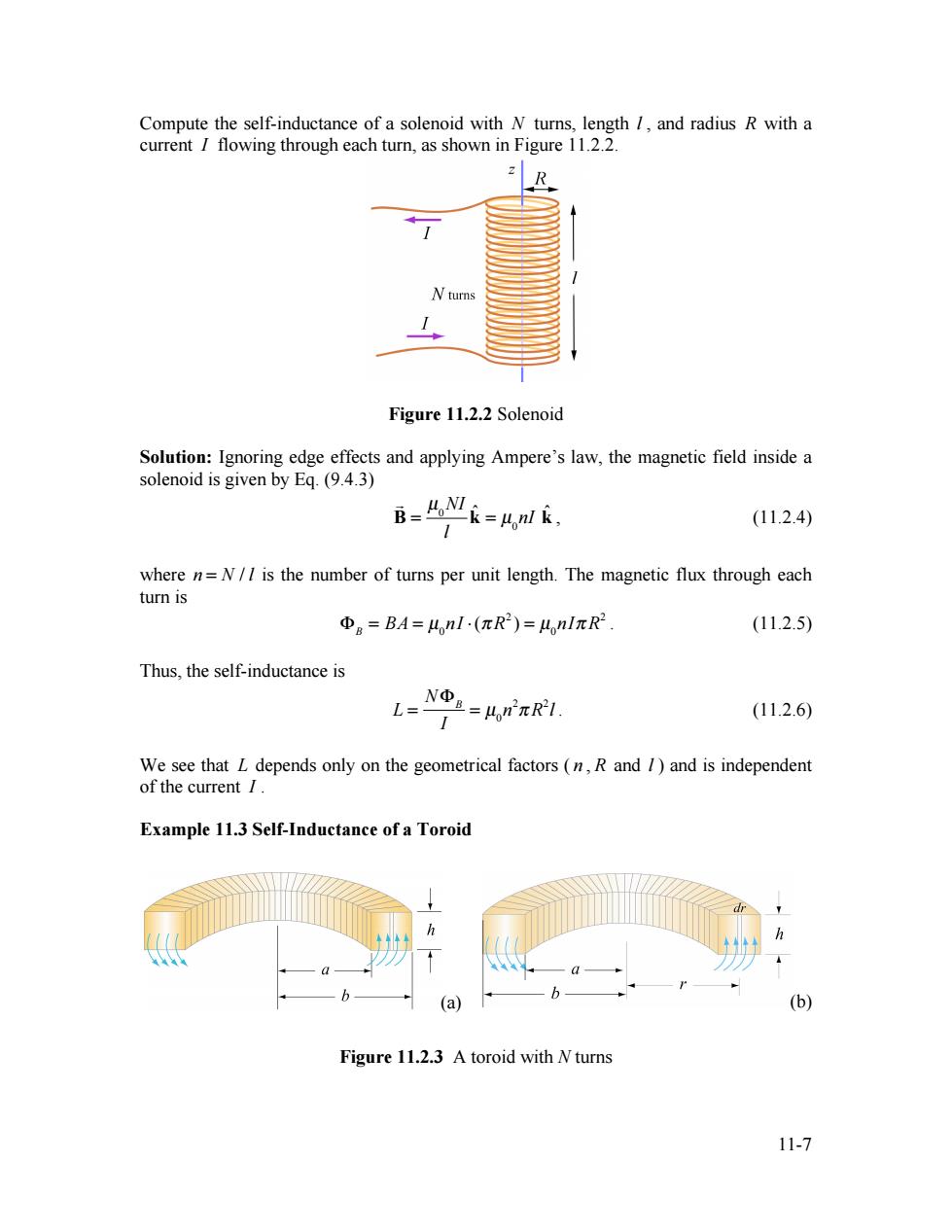
Compute the self-inductance of a solenoid with N turns,length 1,and radius R with a current I flowing through each turn,as shown in Figure 11.2.2. N turns Figure 11.2.2 Solenoid Solution:Ignoring edge effects and applying Ampere's law,the magnetic field inside a solenoid is given by Eq.(9.4.3) B=,M求=4lk, (11.2.4) where n=N//is the number of turns per unit length.The magnetic flux through each turn is Φg=BA=nl(πR2)=4nIπR (11.2.5) Thus,the self-inductance is L-Nou-HnTRI. (11.2.6) We see that L depends only on the geometrical factors(n,R and 1)and is independent of the current / Example 11.3 Self-Inductance of a Toroid (a) (b) Figure 11.2.3 A toroid with N turns 11-711-7 Compute the self-inductance of a solenoid with N turns, length l , and radius R with a current I flowing through each turn, as shown in Figure 11.2.2. Figure 11.2.2 Solenoid Solution: Ignoring edge effects and applying Ampere’s law, the magnetic field inside a solenoid is given by Eq. (9.4.3) ! B = µ0NI l kˆ = µ0nI kˆ , (11.2.4) where n = N / l is the number of turns per unit length. The magnetic flux through each turn is !B = BA = µ0nI "(# R2 ) = µ0nI# R2 . (11.2.5) Thus, the self-inductance is L = N!B I = µ0n 2 " R2 l . (11.2.6) We see that L depends only on the geometrical factors ( n , R and l ) and is independent of the current I . Example 11.3 Self-Inductance of a Toroid (a) (b) Figure 11.2.3 A toroid with N turns