正在加载图片...
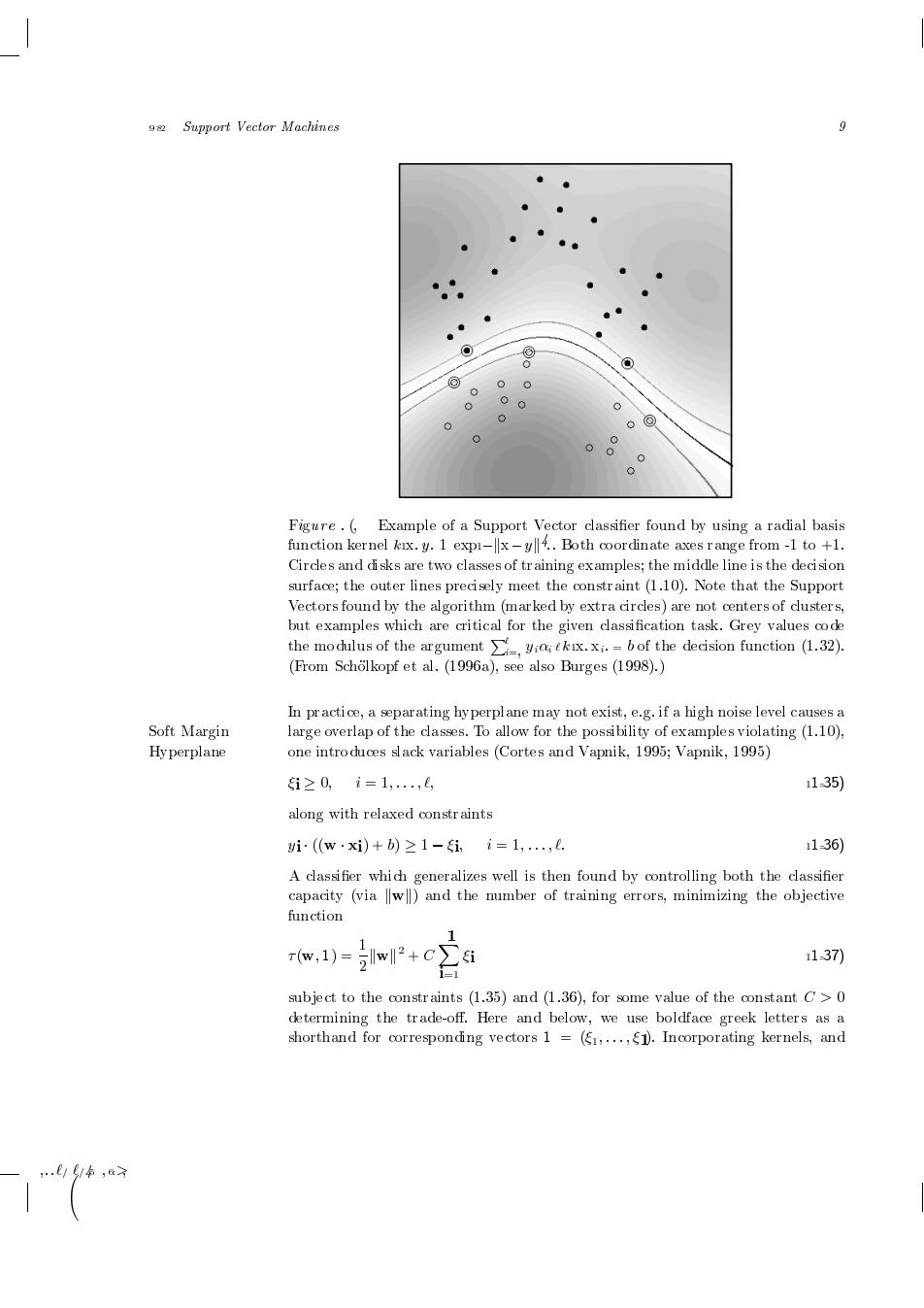
9 Support Vector Machines 9 0 0 0 0 @ 0 Figure.(Example of a Support Vector dlassifier found by using a radial basis function kernel kx.y.1 expi-x-y4..Both coordinate axes range from-1 to +1. Circles and disks are two classes of training examples;the middle line is the decision surface;the outer lines precisely meet the constr aint(1.10).Note that the Support Vectors found by the algorithm(marked by extra circles)are not centers of dlusters, but examples which are critical for the given classification task.Grey values code the modulus of the argument-bof the decision function (1.32). (From Scholkopf et al.(1996a),see also Burges (1998).) In pr actice,a separating hy perplane may not exist,e.g.if a high noise level causes a Soft Margin large overlap of the classes.To allow for the possibility of examples violating (1.10), Hy perplane one introduces slack variables (Cortes and Vapnik,1995;Vapnik,1995) i≥0,i=1,,0, 1135) along with relaxed constr aints yi(w·xi)+b)≥1-i,i=1,,0. 136) A classifier which generalizes well is then found by controlling both the classifier capacity (via w)and the number of training errors,minimizing the objective function T(w,1)= 2w2+c∑i 137) subject to the constr aints (1.35)and(1.36),for some value of the constant C>0 determining the trade-off.Here and below,we use boldface greek letters as a shorthand for corresponding vectors 1 =(61,...,1.Incorporating kernels,and .//6,63 Support Vector Machines Figure Example of a Support Vector classi er found by using a radial basis function kernel kx y expkxyk Both coordinate axes range from to Circles and disks are two classes of training examples the middle line is the decision surface the outer lines precisely meet the constraint Note that the Support Vectors found by the algorithm marked by extra circles are not centers of clusters but examples which are critical for the given classi cation task Grey values code the modulus of the argument P i yii kx xi b of the decision function
From Scholkopf et al
a see also Burges In practice a separating hyperplane may not exist eg if a high noise level causes a Soft Margin large overlap of the classes To allow for the possibility of examples violating Hyperplane one introduces slack variables Cortes and Vapnik Vapnik i i along with relaxed constraints yi w xi b i i A classi er which generalizes well is then found by controlling both the classi er capacity via kwk and the number of training errors minimizing the ob jective function w
kwk CX i i sub ject to the constraints and
for some value of the constant C determining the tradeo Here and below we use boldface greek letters as a shorthand for corresponding vectors Incorporating kernels and���������������������������������������������