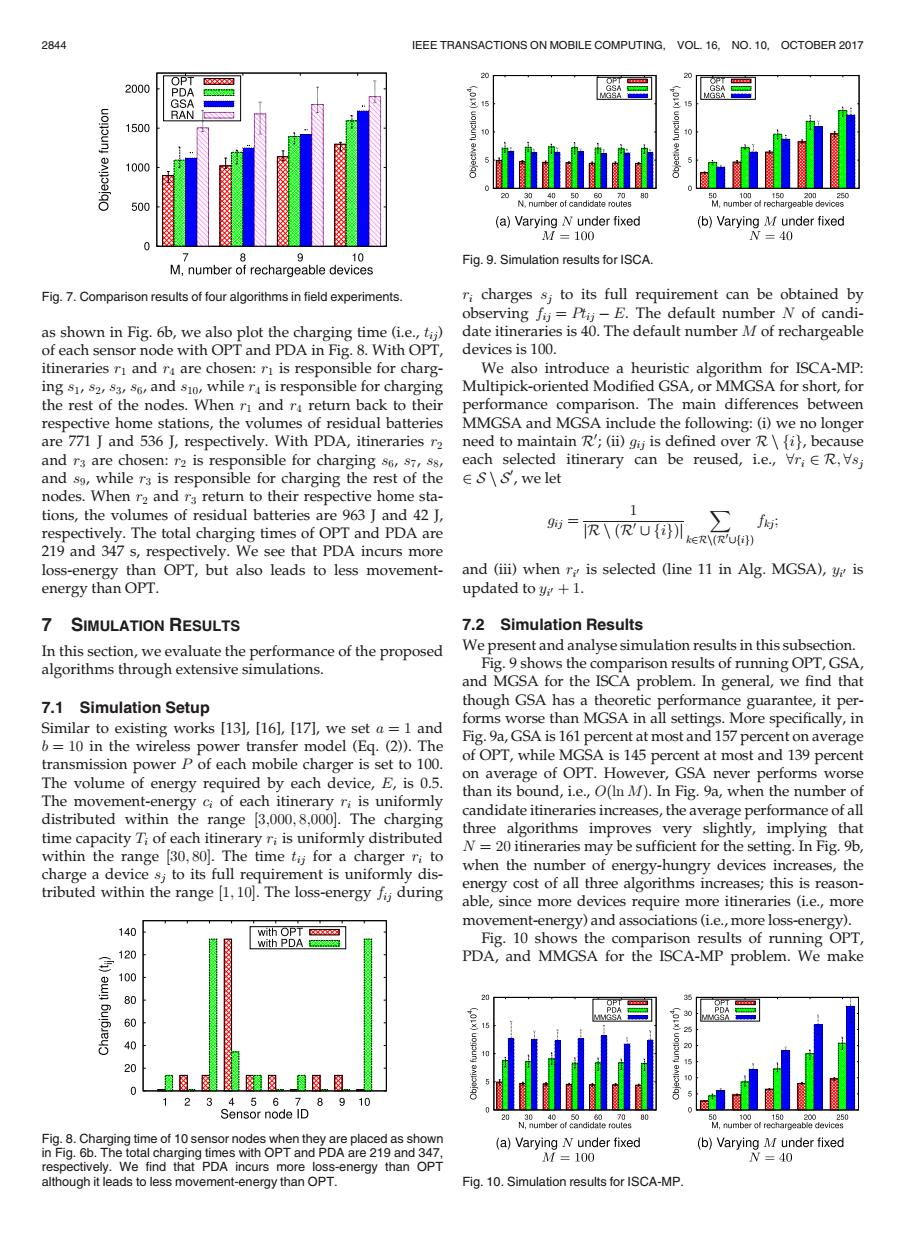
2844 EEE TRANSACTIONS ON MOBILE COMPUTING,VOL.16.NO.10,OCTOBER 2017 2000 OPT PDA GSA 15 RAN 1500 1000 20 500 (a)Varying N under fixed (b)Varying M under fixed M=100 N=40 0 8 10 Fig.9.Simulation results for ISCA M,number of rechargeable devices Fig.7.Comparison results of four algorithms in field experiments. ri charges s;to its full requirement can be obtained by observing fij=Ptij-E.The default number N of candi- as shown in Fig.6b,we also plot the charging time (i.e.,tij) date itineraries is 40.The default number M of rechargeable of each sensor node with OPT and PDA in Fig.8.With OPT, devices is 100. itineraries rI and ra are chosen:ri is responsible for charg- We also introduce a heuristic algorithm for ISCA-MP: ing s1,s2,s3,s6,and s1o,while ra is responsible for charging Multipick-oriented Modified GSA,or MMGSA for short,for the rest of the nodes.When rI and r return back to their performance comparison.The main differences between respective home stations,the volumes of residual batteries MMGSA and MGSA include the following:(i)we no longer are 771 J and 536 J,respectively.With PDA,itineraries r2 need to maintain R';(ii)gij is defined over R fi},because and r3 are chosen:r2 is responsible for charging s6,s7,ss, each selected itinerary can be reused,i.e.,VriER,Vsj and s9,while rs is responsible for charging the rest of the ES\S,we let nodes.When r2 and r3 return to their respective home sta- tions,the volumes of residual batteries are 963 J and 42 J, f respectively.The total charging times of OPT and PDA are 95=R\(UkR) 219 and 347 s,respectively.We see that PDA incurs more loss-energy than OPT,but also leads to less movement- and (iii)when r;is selected (line 11 in Alg.MGSA),y;is energy than OPT. updated to y;+1. 7 SIMULATION RESULTS 7.2 Simulation Results In this section,we evaluate the performance of the proposed We present and analyse simulation results in this subsection. algorithms through extensive simulations. Fig.9 shows the comparison results of running OPT,GSA and MGSA for the ISCA problem.In general,we find that 7.1 Simulation Setup though GSA has a theoretic performance guarantee,it per- Similar to existing works [13],[16],[17],we set a=1 and forms worse than MGSA in all settings.More specifically,in b=10 in the wireless power transfer model (Eq.(2)).The Fig.9a,GSA is 161 percent at most and 157 percent on average transmission power P of each mobile charger is set to 100. of OPT,while MGSA is 145 percent at most and 139 percent The volume of energy required by each device,E,is 0.5. on average of OPT.However,GSA never performs worse than its bound,i.e.,O(In M).In Fig.9a,when the number of The movement-energy ci of each itinerary ri is uniformly distributed within the range [3,000,8,000).The charging candidate itineraries increases,the average performance of all time capacity T;of each itinerary ri is uniformly distributed three algorithms improves very slightly,implying that within the range [30,80].The time ti for a charger ri to N=20 itineraries may be sufficient for the setting.In Fig.9b, charge a device sj to its full requirement is uniformly dis- when the number of energy-hungry devices increases,the tributed within the range[1,10].The loss-energy fij during energy cost of all three algorithms increases;this is reason- able,since more devices require more itineraries (i.e.,more movement-energy)and associations(i.e.,more loss-energy). 140 with OPT with PDA Fig.10 shows the comparison results of running OPT, 120 PDA,and MMGSA for the ISCA-MP problem.We make 100 60 40 0 1 2345678910 Sensor node ID N,number of candidate routes M,number of rechargeable devices Fig.8.Charging time of 10 sensor nodes when they are placed as shown (a)Varying N under fixed (b)Varying M under fixed in Fig.6b.The total charging times with OPT and PDA are 219 and 347 M=100 N=40 respectively.We find that PDA incurs more loss-energy than OPT although it leads to less movement-energy than OPT. Fig.10.Simulation results for ISCA-MP.as shown in Fig. 6b, we also plot the charging time (i.e., tij) of each sensor node with OPT and PDA in Fig. 8. With OPT, itineraries r1 and r4 are chosen: r1 is responsible for charg￾ing s1, s2, s3, s6, and s10, while r4 is responsible for charging the rest of the nodes. When r1 and r4 return back to their respective home stations, the volumes of residual batteries are 771 J and 536 J, respectively. With PDA, itineraries r2 and r3 are chosen: r2 is responsible for charging s6, s7, s8, and s9, while r3 is responsible for charging the rest of the nodes. When r2 and r3 return to their respective home sta￾tions, the volumes of residual batteries are 963 J and 42 J, respectively. The total charging times of OPT and PDA are 219 and 347 s, respectively. We see that PDA incurs more loss-energy than OPT, but also leads to less movement￾energy than OPT. 7 SIMULATION RESULTS In this section, we evaluate the performance of the proposed algorithms through extensive simulations. 7.1 Simulation Setup Similar to existing works [13], [16], [17], we set a ¼ 1 and b ¼ 10 in the wireless power transfer model (Eq. (2)). The transmission power P of each mobile charger is set to 100. The volume of energy required by each device, E, is 0.5. The movement-energy ci of each itinerary ri is uniformly distributed within the range ½3;000; 8;000. The charging time capacity Ti of each itinerary ri is uniformly distributed within the range ½30; 80. The time tij for a charger ri to charge a device sj to its full requirement is uniformly dis￾tributed within the range ½1; 10. The loss-energy fij during ri charges sj to its full requirement can be obtained by observing fij ¼ Ptij  E. The default number N of candi￾date itineraries is 40. The default number M of rechargeable devices is 100. We also introduce a heuristic algorithm for ISCA-MP: Multipick-oriented Modified GSA, or MMGSA for short, for performance comparison. The main differences between MMGSA and MGSA include the following: (i) we no longer need to maintain R0 ; (ii) gij is defined over Rnfig, because each selected itinerary can be reused, i.e., 8ri 2 R; 8sj 2SnS0 , we let gij ¼ 1 jR n ðR0 [ figÞj X k2RnðR0 [figÞ fkj; and (iii) when ri0 is selected (line 11 in Alg. MGSA), yi0 is updated to yi0 þ 1. 7.2 Simulation Results We present and analyse simulation results in this subsection. Fig. 9 shows the comparison results of running OPT, GSA, and MGSA for the ISCA problem. In general, we find that though GSA has a theoretic performance guarantee, it per￾forms worse than MGSA in all settings. More specifically, in Fig. 9a, GSA is 161 percent at most and 157 percent on average of OPT, while MGSA is 145 percent at most and 139 percent on average of OPT. However, GSA never performs worse than its bound, i.e., OðlnMÞ. In Fig. 9a, when the number of candidate itineraries increases, the average performance of all three algorithms improves very slightly, implying that N ¼ 20 itineraries may be sufficient for the setting. In Fig. 9b, when the number of energy-hungry devices increases, the energy cost of all three algorithms increases; this is reason￾able, since more devices require more itineraries (i.e., more movement-energy) and associations (i.e., more loss-energy). Fig. 10 shows the comparison results of running OPT, PDA, and MMGSA for the ISCA-MP problem. We make Fig. 7. Comparison results of four algorithms in field experiments. Fig. 9. Simulation results for ISCA. Fig. 10. Simulation results for ISCA-MP. Fig. 8. Charging time of 10 sensor nodes when they are placed as shown in Fig. 6b. The total charging times with OPT and PDA are 219 and 347, respectively. We find that PDA incurs more loss-energy than OPT although it leads to less movement-energy than OPT. 2844 IEEE TRANSACTIONS ON MOBILE COMPUTING, VOL. 16, NO. 10, OCTOBER 2017