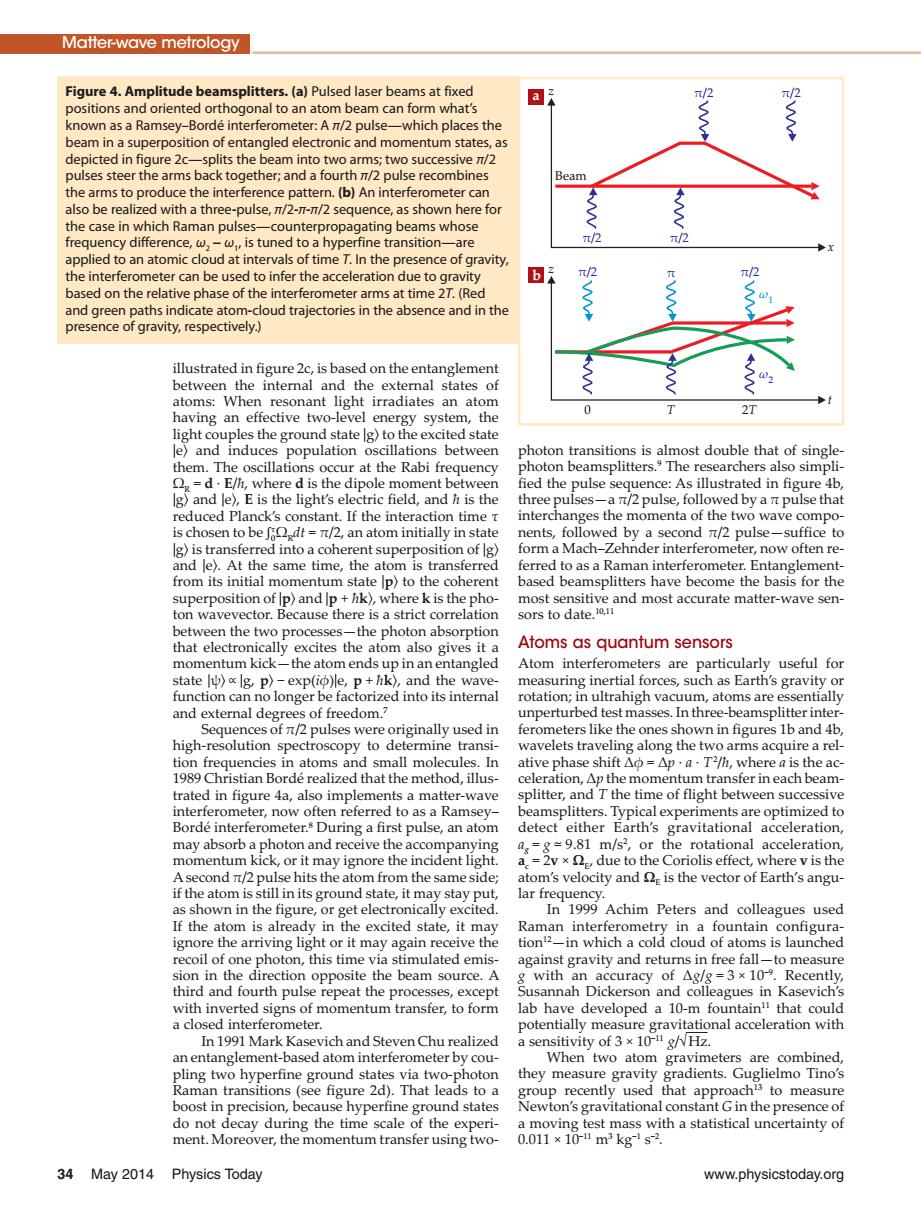
Matter-wave metrology Figure 4.Amplitude beamsplitters.(a)Pulsed laser beams at fixed /2 /2 positions and oriented orthogonal to an atom beam can form what's known as a Ramsey-Borde interferometer:A n/2 pulse-which places the beam in a superposition of entangled electronic and momentum states,as depicted in figure 2c-splits the beam into two arms;two successive n/2 pulses steer the arms back together;and a fourth 7/2 pulse recombines Beam the arms to produce the interference pattern.(b)An interferometer can also be realized with a three-pulse,7/2-7-7/2 sequence,as shown here for the case in which Raman pulses-counterpropagating beams whose frequency difference,w,-w,,is tuned to a hyperfine transition-are π/2 元/2 applied to an atomic cloud at intervals of time T.In the presence of gravity, the interferometer can be used to infer the acceleration due to gravity b π/2 2 based on the relative phase of the interferometer arms at time 27.(Red and green paths indicate atom-cloud trajectories in the absence and in the presence of gravity,respectively.) illustrated in figure 2c,is based on the entanglement between the internal and the external states of atoms:When resonant light irradiates an atom having an effective two-level energy system,the 0 2T light couples the ground state lg)to the excited state le)and induces population oscillations between photon transitions is almost double that of single- them.The oscillations occur at the Rabi frequency photon beamsplitters.The researchers also simpli- =d.E/h,where d is the dipole moment between fied the pulse sequence:As illustrated in figure 4b, Ig)and le),E is the light's electric field,and h is the three pulses-a n/2 pulse,followed by a n pulse that reduced Planck's constant.If the interaction time t interchanges the momenta of the two wave compo- is chosen to be dt =n/2,an atom initially in state nents,followed by a second n/2 pulse-suffice to Ig)is transferred into a coherent superposition of lg) form a Mach-Zehnder interferometer,now often re- and le).At the same time,the atom is transferred ferred to as a Raman interferometer.Entanglement- from its initial momentum state p)to the coherent based beamsplitters have become the basis for the superposition of lp)and lp +hk),where k is the pho- most sensitive and most accurate matter-wave sen- ton wavevector.Because there is a strict correlation sors to date.10.1 between the two processes-the photon absorption that electronically excites the atom also gives it a Atoms as quantum sensors momentum kick-the atom ends up in an entangled Atom interferometers are particularly useful for state o lg,p)-exp(io)le,p+hk),and the wave- measuring inertial forces,such as Earth's gravity or function can no longer be factorized into its internal rotation;in ultrahigh vacuum,atoms are essentially and external degrees of freedom.? unperturbed test masses.In three-beamsplitter inter- Sequences of n/2 pulses were originally used in ferometers like the ones shown in figures 1b and 4b, high-resolution spectroscopy to determine transi- wavelets traveling along the two arms acquire a rel- tion frequencies in atoms and small molecules.In ative phase shift△p=△p·a,TIh,where a is the ac- 1989 Christian Borde realized that the method,illus- celeration,Ap the momentum transfer in each beam- trated in figure 4a,also implements a matter-wave splitter,and T the time of flight between successive interferometer,now often referred to as a Ramsey- beamsplitters.Typical experiments are optimized to Borde interferometer.s During a first pulse,an atom detect either Earth's gravitational acceleration, may absorb a photon and receive the accompanying a=g=9.81 m/s2,or the rotational acceleration, momentum kick,or it may ignore the incident light. a.=2v x,due to the Coriolis effect,where v is the Asecond n/2 pulse hits the atom from the same side; atom's velocity and is the vector of Earth's angu- if the atom is still in its ground state,it may stay put, lar frequency as shown in the figure,or get electronically excited. In 1999 Achim Peters and colleagues used If the atom is already in the excited state,it may Raman interferometry in a fountain configura- ignore the arriving light or it may again receive the tion'2-in which a cold cloud of atoms is launched recoil of one photon,this time via stimulated emis- against gravity and returns in free fall-to measure sion in the direction opposite the beam source.A g with an accuracy of Ag/g=3x109.Recently, third and fourth pulse repeat the processes,except Susannah Dickerson and colleagues in Kasevich's with inverted signs of momentum transfer,to form lab have developed a 10-m fountain!that could a closed interferometer. potentially measure gravitational acceleration with In 1991 Mark Kasevich and Steven Chu realized a sensitivity of 3 x 10 g/Hz. an entanglement-based atom interferometer by cou- When two atom gravimeters are combined, pling two hyperfine ground states via two-photon they measure gravity gradients.Guglielmo Tino's Raman transitions(see figure 2d).That leads to a group recently used that approach'3 to measure boost in precision,because hyperfine ground states Newton's gravitational constant G in the presence of do not decay during the time scale of the experi- a moving test mass with a statistical uncertainty of ment.Moreover,the momentum transfer using two- 0.011×1011m3kgs2. 34 May 2014 Physics Today www.physicstoday.orgillustrated in figure 2c, is based on the entanglement between the internal and the external states of atoms: When resonant light irradiates an atom having an effective two- level energy system, the light couples the ground state ∣g〉 to the excited state ∣e〉 and induces population oscillations between them. The oscillations occur at the Rabi frequency ΩR = d · E/ħ, where d is the dipole moment between ∣g〉 and ∣e〉, E is the light’s electric field, and ħ is the reduced Planck’s constant. If the interaction time τ is chosen to be ∫0 τ ΩRdt = π/2, an atom initially in state ∣g〉 is transferred into a coherent superposition of ∣g〉 and ∣e〉. At the same time, the atom is transferred from its initial momentum state ∣p〉 to the coherent superposition of ∣p〉 and ∣p + ħk〉, where k is the pho￾ton wavevector. Because there is a strict correlation between the two processes—the photon absorption that electronically excites the atom also gives it a momentum kick—the atom ends up in an entangled state ∣ψ〉 ∝ ∣g, p〉 − exp(iϕ)∣e, p + ħk〉, and the wave￾function can no longer be factorized into its internal and external degrees of freedom.7 Sequences of π/2 pulses were originally used in high- resolution spectroscopy to determine transi￾tion frequencies in atoms and small molecules. In 1989 Christian Bordé realized that the method, illus￾trated in figure 4a, also implements a matter- wave interferometer, now often referred to as a Ramsey– Bordé interferometer.8 During a first pulse, an atom may absorb a photon and receive the accompanying momentum kick, or it may ignore the incident light. A second π/2 pulse hits the atom from the same side; if the atom is still in its ground state, it may stay put, as shown in the figure, or get electronically excited. If the atom is already in the excited state, it may ignore the arriving light or it may again receive the recoil of one photon, this time via stimulated emis￾sion in the direction opposite the beam source. A third and fourth pulse repeat the processes, except with inverted signs of momentum transfer, to form a closed interferometer. In 1991 Mark Kasevich and Steven Chu realized an entanglement- based atom interferometer by cou￾pling two hyperfine ground states via two- photon Raman transitions (see figure 2d). That leads to a boost in precision, because hyperfine ground states do not decay during the time scale of the experi￾ment. Moreover, the momentum transfer using two- photon transitions is almost double that of single- photon beamsplitters.9 The researchers also simpli￾fied the pulse sequence: As illustrated in figure 4b, three pulses—a π/2 pulse, followed by a π pulse that interchanges the momenta of the two wave compo￾nents, followed by a second π/2 pulse—suffice to form a Mach–Zehnder interferometer, now often re￾ferred to as a Raman interferometer. Entanglement- based beamsplitters have become the basis for the most sensitive and most accurate matter- wave sen￾sors to date.10,11 Atoms as quantum sensors Atom interferometers are particularly useful for measuring inertial forces, such as Earth’s gravity or rotation; in ultrahigh vacuum, atoms are essentially unperturbed test masses. In three- beamsplitter inter￾ferometers like the ones shown in figures 1b and 4b, wavelets traveling along the two arms acquire a rel￾ative phase shift Δϕ = Δp · a · T2 /ħ, where a is the ac￾celeration, Δp the momentum transfer in each beam￾splitter, and T the time of flight between successive beamsplitters. Typical experiments are optimized to detect either Earth’s gravitational acceleration, ag = g ≃ 9.81 m/s2 , or the rotational acceleration, ac = 2v × ΩE, due to the Coriolis effect, where v is the atom’s velocity and ΩE is the vector of Earth’s angu￾lar frequency. In 1999 Achim Peters and colleagues used Raman interferometry in a fountain configura￾tion12—in which a cold cloud of atoms is launched against gravity and returns in free fall—to measure g with an accuracy of Δg/g = 3 × 10−9. Recently, Susannah Dickerson and colleagues in Kasevich’s lab have developed a 10-m fountain11 that could potentially measure gravitational acceleration with a sensitivity of 3 × 10−11 g/√―Hz. When two atom gravimeters are combined, they measure gravity gradients. Guglielmo Tino’s group recently used that approach13 to measure Newton’s gravitational constant G in the presence of a moving test mass with a statistical uncertainty of 0.011 × 10−11 m3 kg−1 s−2. 34 May 2014 Physics Today www.physicstoday.org Matter-wave metrology π/2 π/2 π/2 π π/2 z π/2 π/2 z x t ω1 ω2 0 T 2T a b Beam Figure 4. Amplitude beamsplitters. (a) Pulsed laser beams at fixed positions and oriented orthogonal to an atom beam can form what’s known as a Ramsey–Bordé interferometer: A π/2 pulse—which places the beam in a superposition of entangled electronic and momentum states, as depicted in figure 2c—splits the beam into two arms; two successive π/2 pulses steer the arms back together; and a fourth π/2 pulse recombines the arms to produce the interference pattern. (b) An interferometer can also be realized with a three-pulse, π/2-π-π/2 sequence, as shown here for the case in which Raman pulses—counterpropagating beams whose frequency difference, ω2 − ω1, is tuned to a hyperfine transition—are applied to an atomic cloud at intervals of time T. In the presence of gravity, the interferometer can be used to infer the acceleration due to gravity based on the relative phase of the interferometer arms at time 2T. (Red and green paths indicate atom-cloud trajectories in the absence and in the presence of gravity, respectively.) This article is copyrighted as indicated in the article. Reuse of AIP content is subject to the terms at: http://scitation.aip.org/termsconditions. Downloaded to IP: 202.120.2.30 On: Thu, 01 May 2014 23:26:12