正在加载图片...
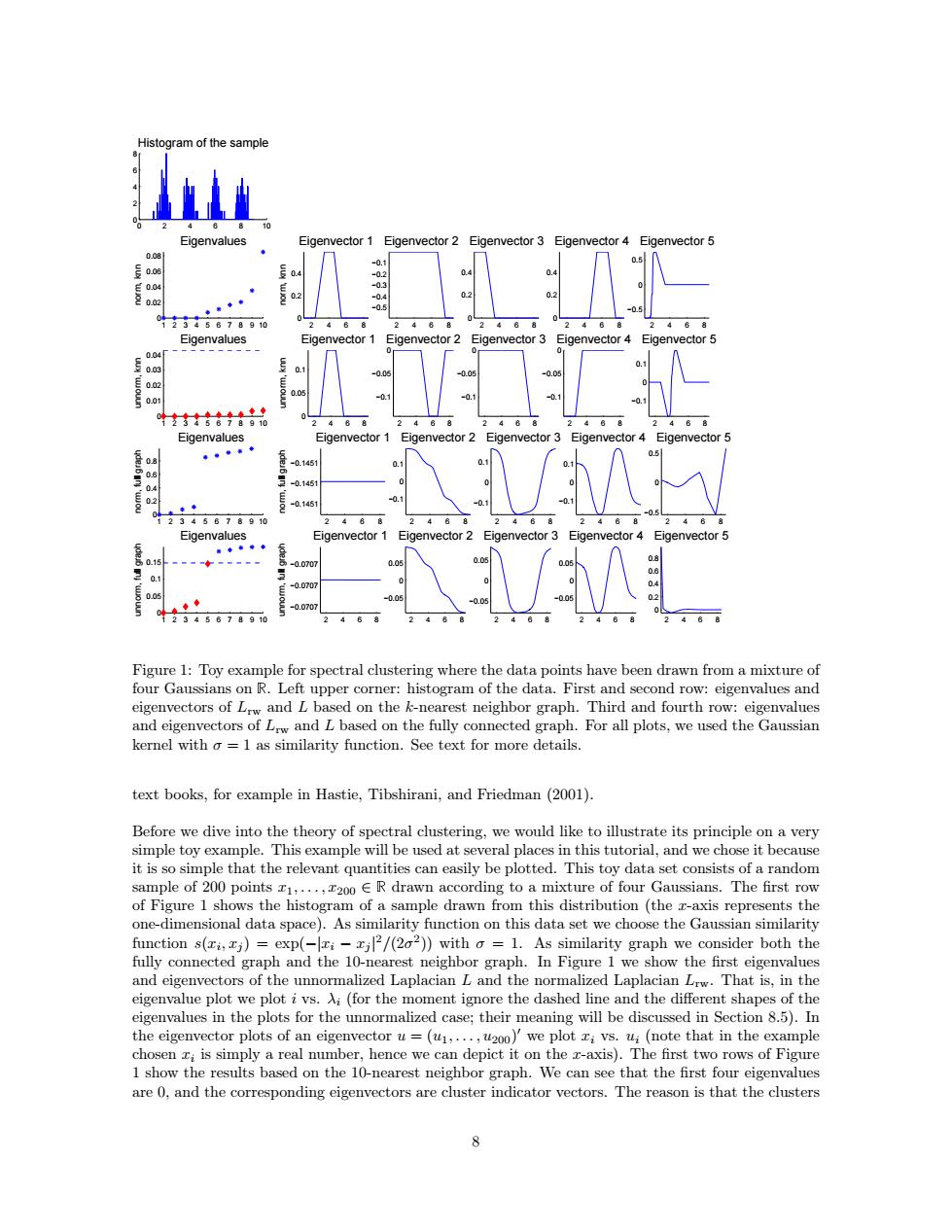
Histogram of the sample Eigenvalues Eigenvector 1 Eigenvector 2 Eigenvector 3 Eigenvector 4 Eigenvector 5 008 0. 0.08 0 E0.0 04支846678910 24含 Eigenvalues Eigenvector 1 Eigenvector 2 Eigenvector 3 Eigenvector 4 Eigenvector 5 0.04 0.03 0.02 品 Eigenvalues Eigenvector 1 Eigenvector 2 Eigenvector 3 Eigenvector 4 Eigenvector 5 08 -0.1451 0 4 -01451 事◆ -0.1451 02345678910 488 Eigenvalues Eigenvector 1 Eigenvector 2 Eigenvector 3 Eigenvector 4 Eigenvector 5 ◆ 0.15 0.0707 0.0 0.1 -0.0707 0.05 -0.0707 345678910 2468 468 Figure 1:Toy example for spectral clustering where the data points have been drawn from a mixture of four Gaussians on R.Left upper corner:histogram of the data.First and second row:eigenvalues and eigenvectors of Lrw and L based on the k-nearest neighbor graph.Third and fourth row:eigenvalues and eigenvectors of Lw and L based on the fully connected graph.For all plots,we used the Gaussian kernel with o=1 as similarity function.See text for more details text books,for example in Hastie,Tibshirani,and Friedman(2001). Before we dive into the theory of spectral clustering,we would like to illustrate its principle on a very simple toy example.This example will be used at several places in this tutorial,and we chose it because it is so simple that the relevant quantities can easily be plotted.This toy data set consists of a random sample of 200 points z1,...,200 ER drawn according to a mixture of four Gaussians.The first row of Figure 1 shows the histogram of a sample drawn from this distribution (the z-axis represents the one-dimensional data space).As similarity function on this data set we choose the Gaussian similarity function s(xi,xj)=exp(-xi-zj2/(202))with o 1.As similarity graph we consider both the fully connected graph and the 10-nearest neighbor graph.In Figure 1 we show the first eigenvalues and eigenvectors of the unnormalized Laplacian L and the normalized Laplacian Lrw.That is,in the eigenvalue plot we plot i vs.Ai(for the moment ignore the dashed line and the different shapes of the eigenvalues in the plots for the unnormalized case;their meaning will be discussed in Section 8.5).In the eigenvector plots of an eigenvector u=(u1,...,u200)we plot zi vs.u;(note that in the example chosen zi is simply a real number,hence we can depict it on the r-axis).The first two rows of Figure 1 show the results based on the 10-nearest neighbor graph.We can see that the first four eigenvalues are 0,and the corresponding eigenvectors are cluster indicator vectors.The reason is that the clusters 80 2 4 6 8 10 0 2 4 6 8 Histogram of the sample 1 2 3 4 5 6 7 8 9 10 0 0.02 0.04 0.06 0.08 Eigenvalues norm, knn 2 4 6 8 0 0.2 0.4 norm, knn Eigenvector 1 2 4 6 8 −0.5 −0.4 −0.3 −0.2 −0.1 Eigenvector 2 2 4 6 8 0 0.2 0.4 Eigenvector 3 2 4 6 8 0 0.2 0.4 Eigenvector 4 2 4 6 8 −0.5 0 0.5 Eigenvector 5 1 2 3 4 5 6 7 8 9 10 0 0.01 0.02 0.03 0.04 Eigenvalues unnorm, knn 2 4 6 8 0 0.05 0.1 unnorm, knn Eigenvector 1 2 4 6 8 −0.1 −0.05 0 Eigenvector 2 2 4 6 8 −0.1 −0.05 0 Eigenvector 3 2 4 6 8 −0.1 −0.05 0 Eigenvector 4 2 4 6 8 −0.1 0 0.1 Eigenvector 5 1 2 3 4 5 6 7 8 9 10 0 0.2 0.4 0.6 0.8 Eigenvalues norm, full graph 2 4 6 8 −0.1451 −0.1451 −0.1451 norm, full graph Eigenvector 1 2 4 6 8 −0.1 0 0.1 Eigenvector 2 2 4 6 8 −0.1 0 0.1 Eigenvector 3 2 4 6 8 −0.1 0 0.1 Eigenvector 4 2 4 6 8 −0.5 0 0.5 Eigenvector 5 1 2 3 4 5 6 7 8 9 10 0 0.05 0.1 0.15 Eigenvalues unnorm, full graph 2 4 6 8 −0.0707 −0.0707 −0.0707 unnorm, full graph Eigenvector 1 2 4 6 8 −0.05 0 0.05 Eigenvector 2 2 4 6 8 −0.05 0 0.05 Eigenvector 3 2 4 6 8 −0.05 0 0.05 Eigenvector 4 2 4 6 8 0 0.2 0.4 0.6 0.8 Eigenvector 5 Figure 1: Toy example for spectral clustering where the data points have been drawn from a mixture of four Gaussians on ❘. Left upper corner: histogram of the data. First and second row: eigenvalues and eigenvectors of Lrw and L based on the k-nearest neighbor graph. Third and fourth row: eigenvalues and eigenvectors of Lrw and L based on the fully connected graph. For all plots, we used the Gaussian kernel with σ = 1 as similarity function. See text for more details. text books, for example in Hastie, Tibshirani, and Friedman (2001). Before we dive into the theory of spectral clustering, we would like to illustrate its principle on a very simple toy example. This example will be used at several places in this tutorial, and we chose it because it is so simple that the relevant quantities can easily be plotted. This toy data set consists of a random sample of 200 points x1, . . . , x200 ∈ ❘ drawn according to a mixture of four Gaussians. The first row of Figure 1 shows the histogram of a sample drawn from this distribution (the x-axis represents the one-dimensional data space). As similarity function on this data set we choose the Gaussian similarity function s(xi , xj ) = exp(−|xi − xj | 2/(2σ 2 )) with σ = 1. As similarity graph we consider both the fully connected graph and the 10-nearest neighbor graph. In Figure 1 we show the first eigenvalues and eigenvectors of the unnormalized Laplacian L and the normalized Laplacian Lrw. That is, in the eigenvalue plot we plot i vs. λi (for the moment ignore the dashed line and the different shapes of the eigenvalues in the plots for the unnormalized case; their meaning will be discussed in Section 8.5). In the eigenvector plots of an eigenvector u = (u1, . . . , u200) 0 we plot xi vs. ui (note that in the example chosen xi is simply a real number, hence we can depict it on the x-axis). The first two rows of Figure 1 show the results based on the 10-nearest neighbor graph. We can see that the first four eigenvalues are 0, and the corresponding eigenvectors are cluster indicator vectors. The reason is that the clusters 8