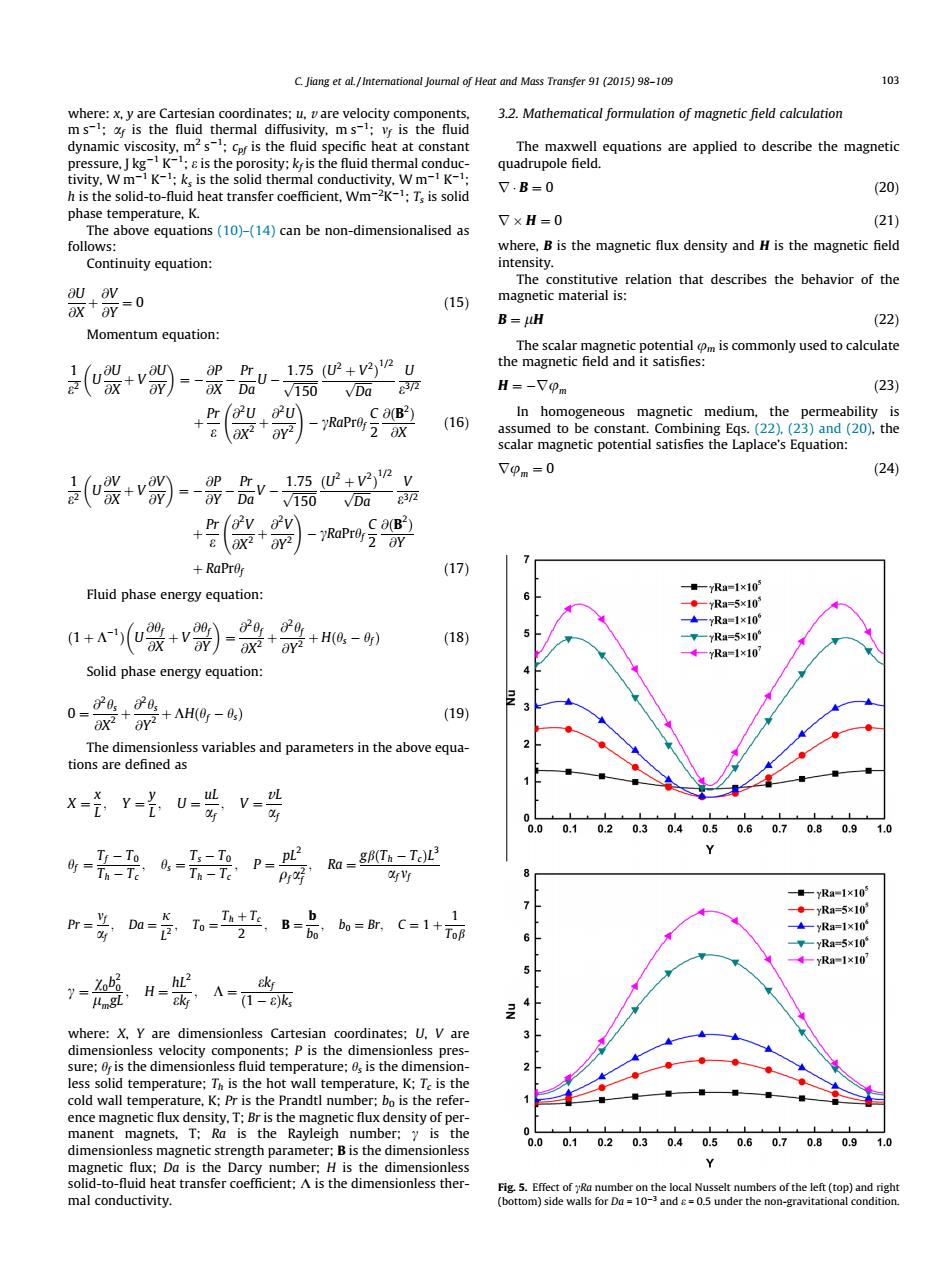
103 s:u.vare 32.Mathematical mogetic field ity.ms the slid-t-u eat T.B=0 (20 又×H=0 心 oleinuiyequaio 贺%0 (15) B-jH (22 Momentum equation: 喂爱-照品 e水mnl +偎别）- (16) 袋+别-器-源心品 Vom-0 (24 +食别- Fluid phase energyeqution: +(微+v器)-股+器+Ha- ✉ Solid phase energy equation: 0-旋祭+Ng- The dimensionless variables and parameters in the above equa tions are defined as x-Y-u-婴v- 1.0 -器严 m-多w-臣'，B-品=所C=1+ 7盛H-器A co wall temperature. 0.0广0102广03广04广0506广07广08广09广10 Chm nm where: x, y are Cartesian coordinates; u, v are velocity components, m s1 ; af is the fluid thermal diffusivity, m s1 ; mf is the fluid dynamic viscosity, m2 s1 ; cpf is the fluid specific heat at constant pressure, J kg1 K1 ; e is the porosity; kf is the fluid thermal conduc￾tivity, W m1 K1 ; ks is the solid thermal conductivity, W m1 K1 ; h is the solid-to-fluid heat transfer coefficient, Wm2 K1 ; Ts is solid phase temperature, K. The above equations (10)–(14) can be non-dimensionalised as follows: Continuity equation: @U @X þ @V @Y ¼ 0 ð15Þ Momentum equation: 1 e2 U @U @X þ V @U @Y  ¼ @P @X Pr DaU 1:75 ffiffiffiffiffiffiffiffiffi 150 p ðU2 þ V2 Þ 1=2 ffiffiffiffiffiffi Da p U e3=2 þ Pr e @2 U @X2 þ @2 U @Y2 ! cRaPrhf C 2 @ðB2 Þ @X ð16Þ 1 e2 U @V @X þ V @V @Y  ¼ @P @Y Pr Da V 1:75 ffiffiffiffiffiffiffiffiffi 150 p ðU2 þ V2 Þ 1=2 ffiffiffiffiffiffi Da p V e3=2 þ Pr e @2 V @X2 þ @2 V @Y2 ! cRaPrhf C 2 @ðB2 Þ @Y þ RaPrhf ð17Þ Fluid phase energy equation: ð1 þ K1 Þ U @hf @X þ V @hf @Y  ¼ @2 hf @X2 þ @2 hf @Y2 þ Hðhs hfÞ ð18Þ Solid phase energy equation: 0 ¼ @2 hs @X2 þ @2 hs @Y2 þ KHðhf hsÞ ð19Þ The dimensionless variables and parameters in the above equa￾tions are defined as X ¼ x L ; Y ¼ y L ; U ¼ uL af ; V ¼ vL af hf ¼ Tf T0 Th Tc ; hs ¼ Ts T0 Th Tc ; P ¼ pL2 qf a2 f ; Ra ¼ gbðTh TcÞL3 af mf Pr ¼ mf af ; Da ¼ j L2 ; T0 ¼ Th þ Tc 2 ; B ¼ b b0 ; b0 ¼ Br; C ¼ 1 þ 1 T0b c ¼ v0b2 0 lmgL ; H ¼ hL2 ekf ; K ¼ ekf ð1 eÞks where: X, Y are dimensionless Cartesian coordinates; U, V are dimensionless velocity components; P is the dimensionless pres￾sure; hf is the dimensionless fluid temperature; hs is the dimension￾less solid temperature; Th is the hot wall temperature, K; Tc is the cold wall temperature, K; Pr is the Prandtl number; b0 is the refer￾ence magnetic flux density, T; Br is the magnetic flux density of per￾manent magnets, T; Ra is the Rayleigh number; c is the dimensionless magnetic strength parameter; B is the dimensionless magnetic flux; Da is the Darcy number; H is the dimensionless solid-to-fluid heat transfer coefficient; K is the dimensionless ther￾mal conductivity. 3.2. Mathematical formulation of magnetic field calculation The maxwell equations are applied to describe the magnetic quadrupole field. r B ¼ 0 ð20Þ r  H ¼ 0 ð21Þ where, B is the magnetic flux density and H is the magnetic field intensity. The constitutive relation that describes the behavior of the magnetic material is: B ¼ lH ð22Þ The scalar magnetic potential um is commonly used to calculate the magnetic field and it satisfies: H ¼ rum ð23Þ In homogeneous magnetic medium, the permeability is assumed to be constant. Combining Eqs. (22), (23) and (20), the scalar magnetic potential satisfies the Laplace’s Equation: rum ¼ 0 ð24Þ Fig. 5. Effect of cRa number on the local Nusselt numbers of the left (top) and right (bottom) side walls for Da = 103 and e = 0.5 under the non-gravitational condition. C. Jiang et al. / International Journal of Heat and Mass Transfer 91 (2015) 98–109 103