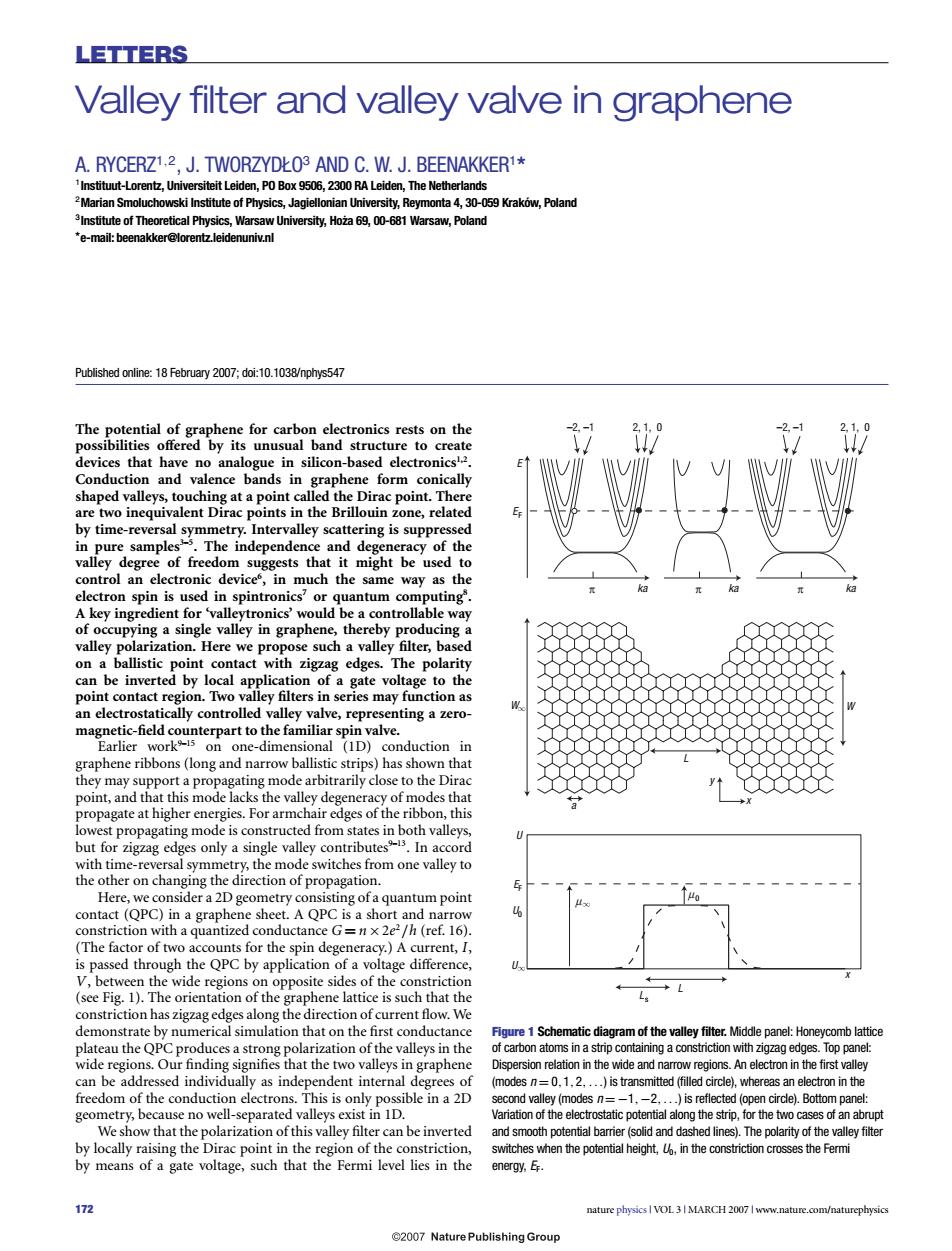
LETTERS Valley filter and valley valve in graphene A.RYCERZ12.J.TWORZYDLO3 AND C.W.J.BEENAKKER1* 'Instituut-Lorentz,Universiteit Leiden,PO Box 9506,2300 RA Leiden,The Netherlands 2Marian Smoluchowski Institute of Physics,Jagiellonian University,Reymonta 4,30-059 Krakow,Poland 3Institute of Theoretical Physics,Warsaw University,Hoza 69,00-681 Warsaw,Poland *e-mail:beenakker@lorentz.leidenuniv.nl Published online:18 February 2007;doi:10.1038/nphys547 The potential of graphene for carbon electronics rests on the possibilities offered by its unusual band structure to create devices that have no analogue in silicon-based electronics 2. Conduction and valence bands in graphene form conically shaped valleys,touching at a point called the Dirac point.There are two inequivalent Dirac points in the Brillouin zone,related by time-reversal symmetry.Intervalley scattering is suppressed in pure samples'.The independence and degeneracy of the valley degree of freedom suggests that it might be used to control an electronic device,in much the same way as the electron spin is used in spintronics'or quantum computing A key ingredient for 'valleytronics'would be a controllable way of occupying a single valley in graphene,thereby producing a valley polarization.Here we propose such a valley filter,based on a ballistic point contact with zigzag edges.The polarity can be inverted by local application of a gate voltage to the point contact region.Two valley filters in series may function as an electrostatically controlled valley valve,representing a zero- magnetic-field counterpart to the familiar spin valve. Earlier work"-15 on one-dimensional (1D)conduction in graphene ribbons(long and narrow ballistic strips)has shown that they may support a propagating mode arbitrarily close to the Dirac point,and that this mode lacks the valley degeneracy of modes that propagate at higher energies.For armchair edges of the ribbon,this lowest propagating mode is constructed from states in both valleys, but for zigzag edges only a single valley contributes15.In accord with time-reversal symmetry,the mode switches from one valley to the other on changing the direction of propagation. Here,we consider a 2D geometry consisting of a quantum point 0 contact(QPC)in a graphene sheet.A QPC is a short and narrow constriction with a quantized conductance G=n x 2e2/h (ref.16). (The factor of two accounts for the spin degeneracy.)A current,I, is passed through the QPC by application of a voltage difference, V,between the wide regions on opposite sides of the constriction (see Fig.1).The orientation of the graphene lattice is such that the constriction has zigzag edges along the direction of current flow.We demonstrate by numerical simulation that on the first conductance Figure 1 Schematic diagram of the valley filter.Middle panel:Honeycomb lattice plateau the QPC produces a strong polarization of the valleys in the of carbon atoms in a strip containing a constriction with zigzag edges.Top panel: wide regions.Our finding signifies that the two valleys in graphene Dispersion relation in the wide and narrow regions.An electron in the first valley can be addressed individually as independent internal degrees of (modes n=0,1.2,...)is transmitted (filled circle),whereas an electron in the freedom of the conduction electrons.This is only possible in a 2D second valley (modes n=-1.-2,...)is reflected (open circle).Bottom panel: geometry,because no well-separated valleys exist in 1D. Variation of the electrostatic potential along the strip,for the two cases of an abrupt We show that the polarization of this valley filter can be inverted and smooth potential barrier(solid and dashed lines).The polarity of the valley filter by locally raising the Dirac point in the region of the constriction, switches when the potential height,in the constriction crosses the Fermi by means of a gate voltage,such that the Fermi level lies in the energy,E. 172 nature physics I VOL 3|MARCH 2007I www.nature.com/naturephysics 2007 Nature Publishing GroupLETTERS Valley filter and valley valve in graphene A. RYCERZ1,2, J. TWORZYDŁO3 AND C. W. J. BEENAKKER1* 1Instituut-Lorentz, Universiteit Leiden, PO Box 9506, 2300 RA Leiden, The Netherlands 2Marian Smoluchowski Institute of Physics, Jagiellonian University, Reymonta 4, 30-059 Krakow, Poland ´ 3Institute of Theoretical Physics, Warsaw University, Ho˙za 69, 00-681 Warsaw, Poland *e-mail: beenakker@lorentz.leidenuniv.nl Published online: 18 February 2007; doi:10.1038/nphys547 The potential of graphene for carbon electronics rests on the possibilities offered by its unusual band structure to create devices that have no analogue in silicon-based electronics1,2. Conduction and valence bands in graphene form conically shaped valleys, touching at a point called the Dirac point. There are two inequivalent Dirac points in the Brillouin zone, related by time-reversal symmetry. Intervalley scattering is suppressed in pure samples3–5. The independence and degeneracy of the valley degree of freedom suggests that it might be used to control an electronic device6 , in much the same way as the electron spin is used in spintronics7 or quantum computing8 . A key ingredient for ‘valleytronics’ would be a controllable way of occupying a single valley in graphene, thereby producing a valley polarization. Here we propose such a valley filter, based on a ballistic point contact with zigzag edges. The polarity can be inverted by local application of a gate voltage to the point contact region. Two valley filters in series may function as an electrostatically controlled valley valve, representing a zero￾magnetic-field counterpart to the familiar spin valve. Earlier work9–15 on one-dimensional (1D) conduction in graphene ribbons (long and narrow ballistic strips) has shown that they may support a propagating mode arbitrarily close to the Dirac point, and that this mode lacks the valley degeneracy of modes that propagate at higher energies. For armchair edges of the ribbon, this lowest propagating mode is constructed from states in both valleys, but for zigzag edges only a single valley contributes9–13. In accord with time-reversal symmetry, the mode switches from one valley to the other on changing the direction of propagation. Here, we consider a 2D geometry consisting of a quantum point contact (QPC) in a graphene sheet. A QPC is a short and narrow constriction with a quantized conductance G = n×2e2 /h (ref. 16). (The factor of two accounts for the spin degeneracy.) A current, I, is passed through the QPC by application of a voltage difference, V, between the wide regions on opposite sides of the constriction (see Fig. 1). The orientation of the graphene lattice is such that the constriction has zigzag edges along the direction of current flow. We demonstrate by numerical simulation that on the first conductance plateau the QPC produces a strong polarization of the valleys in the wide regions. Our finding signifies that the two valleys in graphene can be addressed individually as independent internal degrees of freedom of the conduction electrons. This is only possible in a 2D geometry, because no well-separated valleys exist in 1D. We show that the polarization of this valley filter can be inverted by locally raising the Dirac point in the region of the constriction, by means of a gate voltage, such that the Fermi level lies in the –2, –1 2, 1, 0 –2, –1 2, 1, 0 π ka π ka π ka a L W x y x L μ μ 0 Ls U EF U U0 E EF W Figure 1 Schematic diagram of the valley filter. Middle panel: Honeycomb lattice of carbon atoms in a strip containing a constriction with zigzag edges. Top panel: Dispersion relation in the wide and narrow regions. An electron in the first valley (modes n = 0,1,2,...) is transmitted (filled circle), whereas an electron in the second valley (modes n = −1,−2,...) is reflected (open circle). Bottom panel: Variation of the electrostatic potential along the strip, for the two cases of an abrupt and smooth potential barrier (solid and dashed lines). The polarity of the valley filter switches when the potential height, U0, in the constriction crosses the Fermi energy, EF. 172 nature physics VOL 3 MARCH 2007 www.nature.com/naturephysics Untitled-1 1 13/2/07, 12:35:49 pm