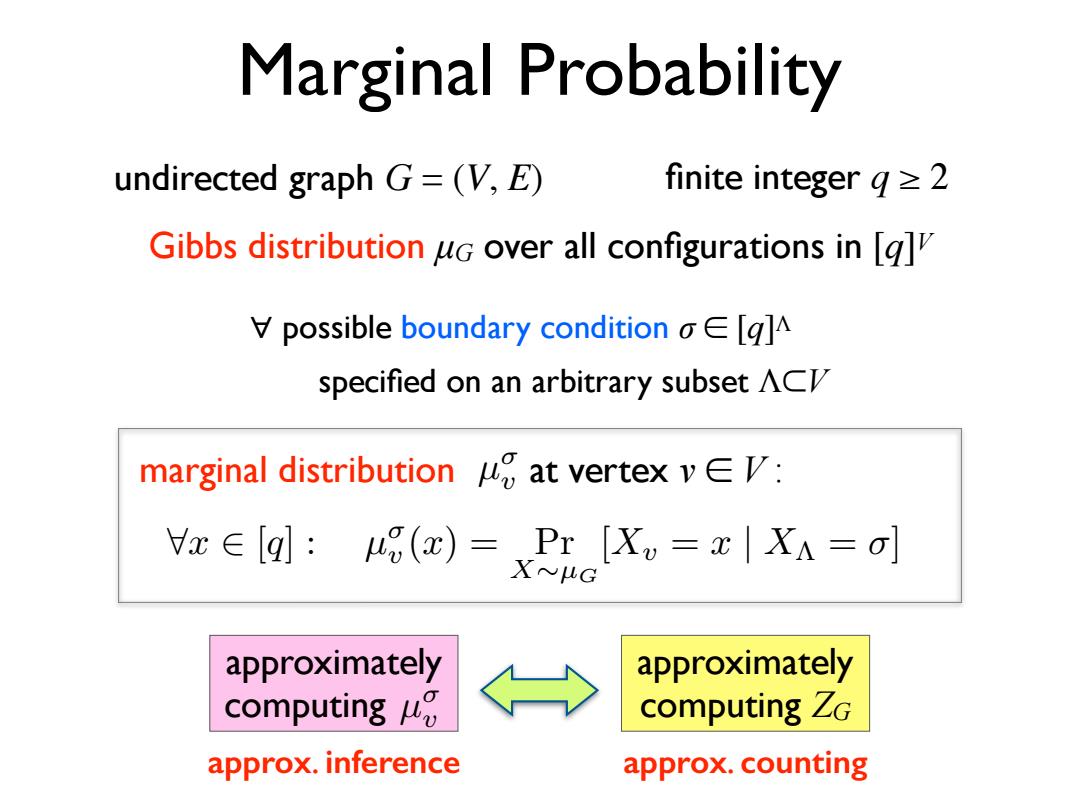
Marginal Probability undirected graph G=(V,E) finite integer q≥2 Gibbs distribution uG over all configurations in [g] V possible boundary condition o E [g]A specified on an arbitrary subset ACD marginal distribution g at vertex vEV: x∈[q]：%(x)=Pr[Xu=x|XA=o] XouG approximately approximately computingu computing ZG approx.inference approx.countingMarginal Probability Gibbs distribution µG over all configurations in [q]V undirected graph G = (V, E) finite integer q ≥ 2 specified on an arbitrary subset Λ⊂V ∀ possible boundary condition σ ∈ [q]Λ marginal distribution at vertex µ v ∈ V : ￾ v 8x 2 [q] : µ￾ v (x) = Pr X⇠µG [Xv = x | X⇤ = ￾] approximately computing µ￾ v approximately computing ZG approx. inference approx. counting