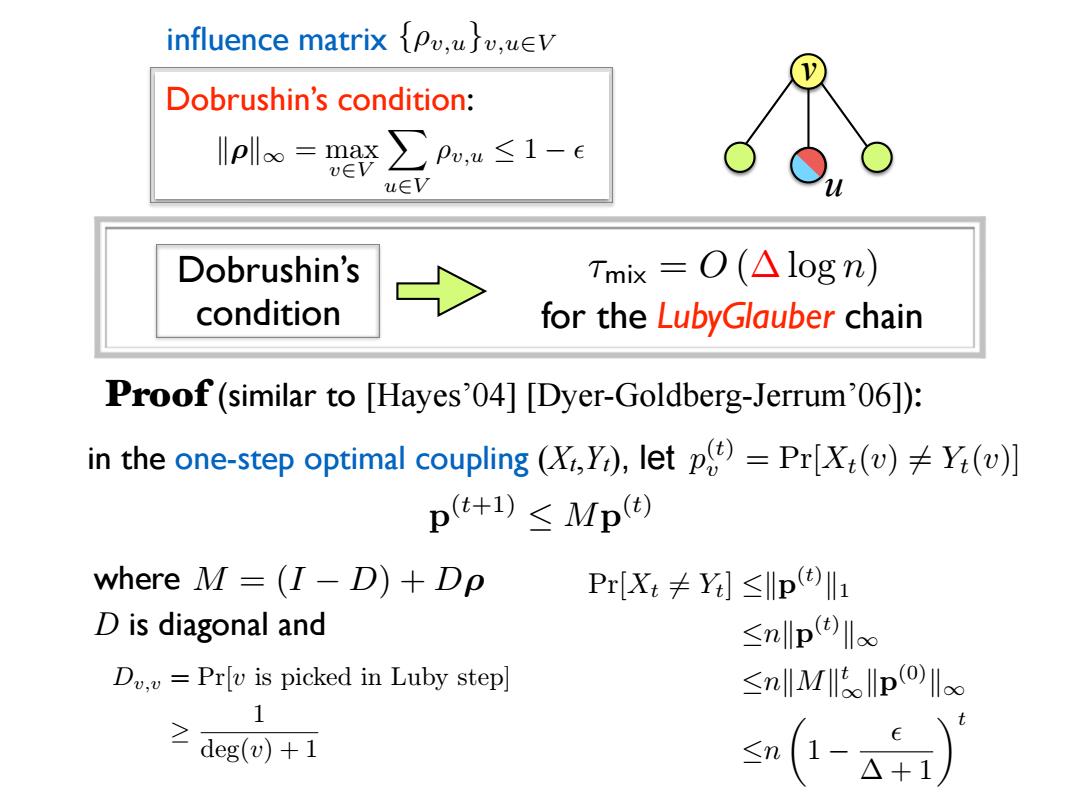
influence matrix {Pv,u,uv Dobrushin's condition: lple=my∑pe,u≤1-e vEV u∈V Dobrushin's Tmx=O(△logn) condition for the LubyGlauber chain Proof(similar to [Hayes'04][Dyer-Goldberg-Jerrum'06]): in the one-step optimal coupling(X,Y),let p)=Pr[x(v)Y(v)] pt+)≤Mp where M=(I-D)+Dp Pr[Xt≠YW≤Ipl1 D is diagonal and ≤nllp D.=Prv is picked in Luby step] ≤p()‖x 1 之deg(u)+1 S(1-A41)Dobrushin’s condition: k⇢k1 = max v2V X u2V ⇢v,u  1 ￾ ✏ influence matrix {⇢v,u }v,u2V u v Dobrushin’s condition for the LubyGlauber chain ⌧mix = O (￾ log n) Dv,v = Pr[v is picked in Luby step] ￾ 1 deg(v)+1 D is diagonal and p(t) in the one-step optimal coupling (Xt,Yt), let v = Pr[Xt(v) 6= Yt(v)] where Proof (similar to [Hayes’04] [Dyer-Goldberg-Jerrum’06]): p(t+1)  Mp(t) Pr[Xt 6= Yt] kp(t) k1 nkp(t) k1 nkMkt 1kp(0)k1 n ✓ 1 ￾ ✏ ￾ + 1◆t M = (I ￾ D) + D⇢