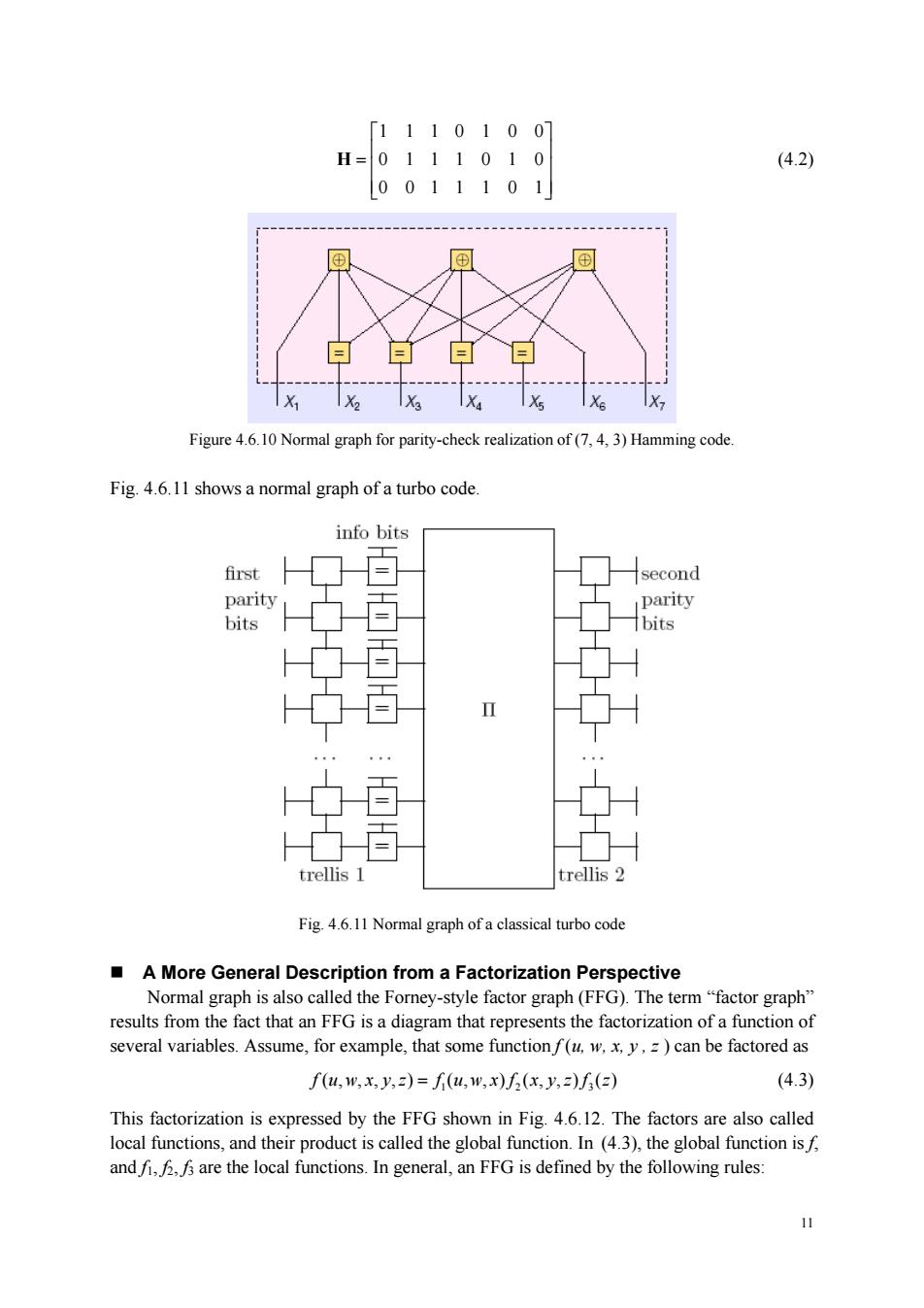
[1110100 H=0111010 (4.2) [0011101 X X X Figure 6.10 Normal graph for parity-check realization of (3)Hamming code Fig.4.6.11 shows a normal graph of a turbo code. info bits first second parity parity bits 百 bits 百 百 trellis 1 trellis 2 Fig 4.6.11 Normal graph ofa classical turbo code A More General Description from a Factorization Perspective Normal graph is also called the Forney-style factor graph(FFG).The term"factor graph" results from the fact that an FFG is a diagram that represents the factorization of a function of several variables.Assume,for example,that some functionf(u.x.y.=)can be factored as f(,w,x,八，)=fu,w,x)(x,)(e) (4.3) This factorization is expressed by the FFG shown in Fig.4.6.12.The factors are also called local functions,and their product is called the global function.In (4.3),the global function isf andi,are the local functions.In general,an FFG is defined by the following rules: 11 11 1110100 0111010 0011101 ⎡ ⎤ ⎢ ⎥ = ⎣ ⎦ H (4.2) Figure 4.6.10 Normal graph for parity-check realization of (7, 4, 3) Hamming code. Fig. 4.6.11 shows a normal graph of a turbo code. Fig. 4.6.11 Normal graph of a classical turbo code „ A More General Description from a Factorization Perspective Normal graph is also called the Forney-style factor graph (FFG). The term “factor graph” results from the fact that an FFG is a diagram that represents the factorization of a function of several variables. Assume, for example, that some function f (u, w, x, y , z ) can be factored as 1 23 f (, , ,) (, , ) (, ,) () uwxyz f uwx f xyz f z = (4.3) This factorization is expressed by the FFG shown in Fig. 4.6.12. The factors are also called local functions, and their product is called the global function. In (4.3), the global function is f, and f1, f2, f3 are the local functions. In general, an FFG is defined by the following rules: