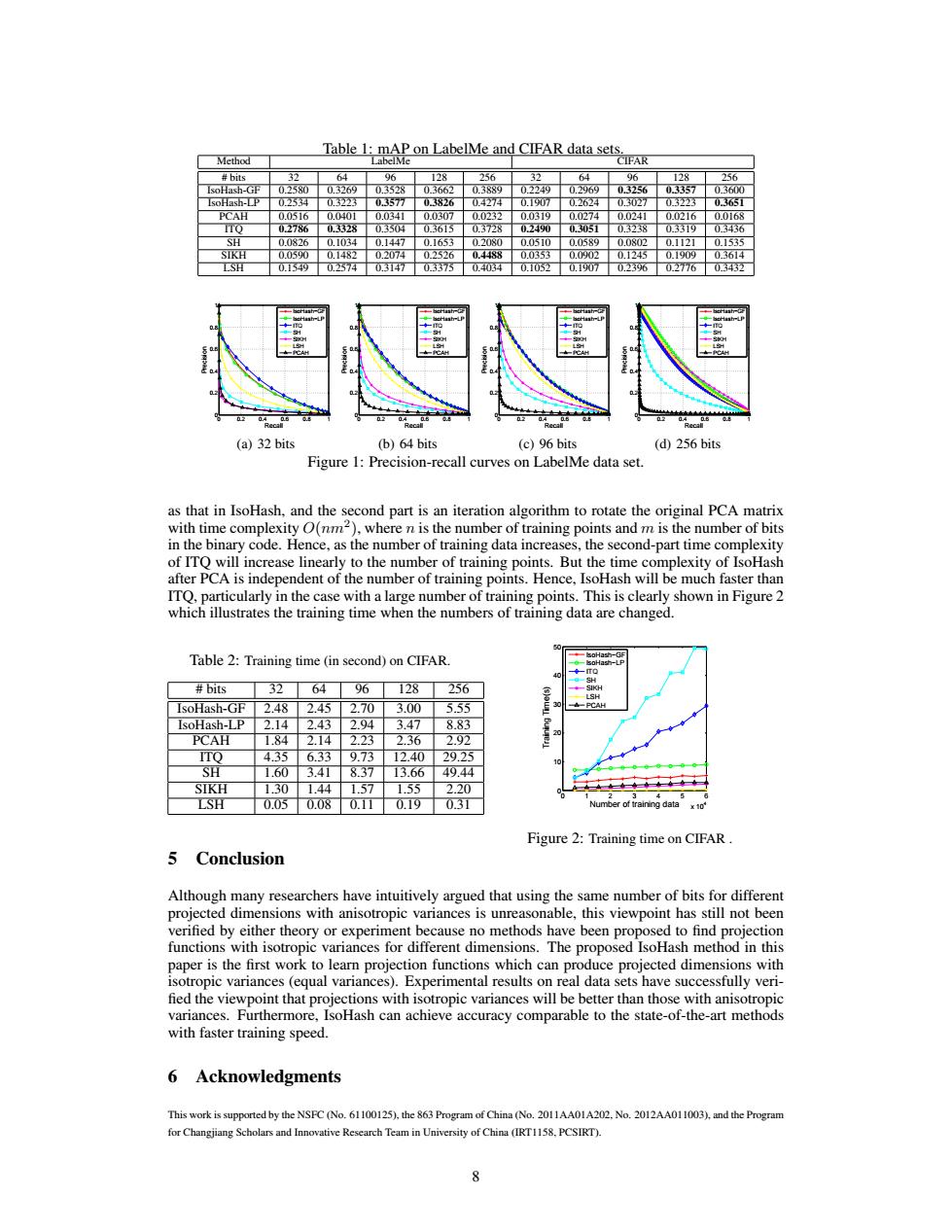
Table 1:mAP on LabelMe and CIFAR data sets Method labelMe IFAR #bits 32 64 96 1)8 56 4 06 18 256 IsoHash-GF 0.25800.3269 0.3528 03662 03889 0.2249 0.2969 0.3256 03357 03600 IsoHash-LP 0重4■ 0.3223 0.3577 03826 0.4274 0.I907 0.2624 0.3027 0.3223 PCAH 00516 00401 00341 00307 00232 00319 00274 00241 00216 00168 02786 0328 0.3504 0.615 03728 0.2490 0305 0.3238 0.3319 0346 SH 0.0826 0.1034 0.1447 0.1653 0.2080 0.0510 0.0589 00802 0.1121 0.1535 SIKH 0.0590 ■0.1482 0.2074 0.2526 0.4488 0.0353 0.0902 0.1245 0.1909 0.3614 LSH 0.15490.2574 0.3147 0375 0.4034 0.1052 0.1907 0.2396 0.2776 03432 (a)32 bits (b)64 bits (c)96 bits (d)256 bits Figure 1:Precision-recall curves on LabelMe data set. as that in IsoHash,and the second part is an iteration algorithm to rotate the original PCA matrix with time complexity O(nm),where n is the number of training points and m is the number of bits in the binary code.Hence,as the number of training data increases,the second-part time complexity of ITQ will increase linearly to the number of training points.But the time complexity of IsoHash after PCA is independent of the number of training points.Hence,IsoHash will be much faster than ITQ,particularly in the case with a large number of training points.This is clearly shown in Figure 2 which illustrates the training time when the numbers of training data are changed. Table 2:Training time(in second)on CIFAR. #bits 32 64 96 128256 IsoHash-GF 2.48 2.452.70 3.00 5.55 CAH IsoHash-LP 2.14 2.43 2.94 3.47 8.83 PCAH 1.84 2.14 2.23 2.36 2.92 ITQ 4.35 6.33 9.73 12.40 29.25 SH 1.60 3.41 8.37 13.66 49.44 SIKH 1.30 1.44 1.57 1.55 2.20 LSH 0.050.08 0.11 0.19 0.31 of training data x10 Figure 2:Training time on CIFAR 5 Conclusion Although many researchers have intuitively argued that using the same number of bits for different projected dimensions with anisotropic variances is unreasonable,this viewpoint has still not been verified by either theory or experiment because no methods have been proposed to find projection functions with isotropic variances for different dimensions.The proposed IsoHash method in this paper is the first work to learn projection functions which can produce projected dimensions with isotropic variances (equal variances).Experimental results on real data sets have successfully veri- fied the viewpoint that projections with isotropic variances will be better than those with anisotropic variances.Furthermore,IsoHash can achieve accuracy comparable to the state-of-the-art methods with faster training speed. 6 Acknowledgments This work is supported by the NSFC (No.61100125),the 863 Program of China (No.2011AA01A202,No.2012AA011003),and the Program for Changjiang Scholars and Innovative Research Team in University of China (IRT1158.PCSIRT)Table 1: mAP on LabelMe and CIFAR data sets. Method LabelMe CIFAR # bits 32 64 96 128 256 32 64 96 128 256 IsoHash-GF 0.2580 0.3269 0.3528 0.3662 0.3889 0.2249 0.2969 0.3256 0.3357 0.3600 IsoHash-LP 0.2534 0.3223 0.3577 0.3826 0.4274 0.1907 0.2624 0.3027 0.3223 0.3651 PCAH 0.0516 0.0401 0.0341 0.0307 0.0232 0.0319 0.0274 0.0241 0.0216 0.0168 ITQ 0.2786 0.3328 0.3504 0.3615 0.3728 0.2490 0.3051 0.3238 0.3319 0.3436 SH 0.0826 0.1034 0.1447 0.1653 0.2080 0.0510 0.0589 0.0802 0.1121 0.1535 SIKH 0.0590 0.1482 0.2074 0.2526 0.4488 0.0353 0.0902 0.1245 0.1909 0.3614 LSH 0.1549 0.2574 0.3147 0.3375 0.4034 0.1052 0.1907 0.2396 0.2776 0.3432 0 0.2 0.4 0.6 0.8 1 0 0.2 0.4 0.6 0.8 1 Recall Precision IsoHash−GF IsoHash−LP ITQ SH SIKH LSH PCAH (a) 32 bits 0 0.2 0.4 0.6 0.8 1 0 0.2 0.4 0.6 0.8 1 Recall Precision IsoHash−GF IsoHash−LP ITQ SH SIKH LSH PCAH (b) 64 bits 0 0.2 0.4 0.6 0.8 1 0 0.2 0.4 0.6 0.8 1 Recall Precision IsoHash−GF IsoHash−LP ITQ SH SIKH LSH PCAH (c) 96 bits 0 0.2 0.4 0.6 0.8 1 0 0.2 0.4 0.6 0.8 1 Recall Precision IsoHash−GF IsoHash−LP ITQ SH SIKH LSH PCAH (d) 256 bits Figure 1: Precision-recall curves on LabelMe data set. as that in IsoHash, and the second part is an iteration algorithm to rotate the original PCA matrix with time complexity O(nm2 ), where n is the number of training points and m is the number of bits in the binary code. Hence, as the number of training data increases, the second-part time complexity of ITQ will increase linearly to the number of training points. But the time complexity of IsoHash after PCA is independent of the number of training points. Hence, IsoHash will be much faster than ITQ, particularly in the case with a large number of training points. This is clearly shown in Figure 2 which illustrates the training time when the numbers of training data are changed. Table 2: Training time (in second) on CIFAR. # bits 32 64 96 128 256 IsoHash-GF 2.48 2.45 2.70 3.00 5.55 IsoHash-LP 2.14 2.43 2.94 3.47 8.83 PCAH 1.84 2.14 2.23 2.36 2.92 ITQ 4.35 6.33 9.73 12.40 29.25 SH 1.60 3.41 8.37 13.66 49.44 SIKH 1.30 1.44 1.57 1.55 2.20 LSH 0.05 0.08 0.11 0.19 0.31 0 1 2 3 4 5 6 x 104 0 10 20 30 40 50 Number of training data Training Time(s) IsoHash−GF IsoHash−LP ITQ SH SIKH LSH PCAH Figure 2: Training time on CIFAR . 5 Conclusion Although many researchers have intuitively argued that using the same number of bits for different projected dimensions with anisotropic variances is unreasonable, this viewpoint has still not been verified by either theory or experiment because no methods have been proposed to find projection functions with isotropic variances for different dimensions. The proposed IsoHash method in this paper is the first work to learn projection functions which can produce projected dimensions with isotropic variances (equal variances). Experimental results on real data sets have successfully veri- fied the viewpoint that projections with isotropic variances will be better than those with anisotropic variances. Furthermore, IsoHash can achieve accuracy comparable to the state-of-the-art methods with faster training speed. 6 Acknowledgments This work is supported by the NSFC (No. 61100125), the 863 Program of China (No. 2011AA01A202, No. 2012AA011003), and the Program for Changjiang Scholars and Innovative Research Team in University of China (IRT1158, PCSIRT). 8