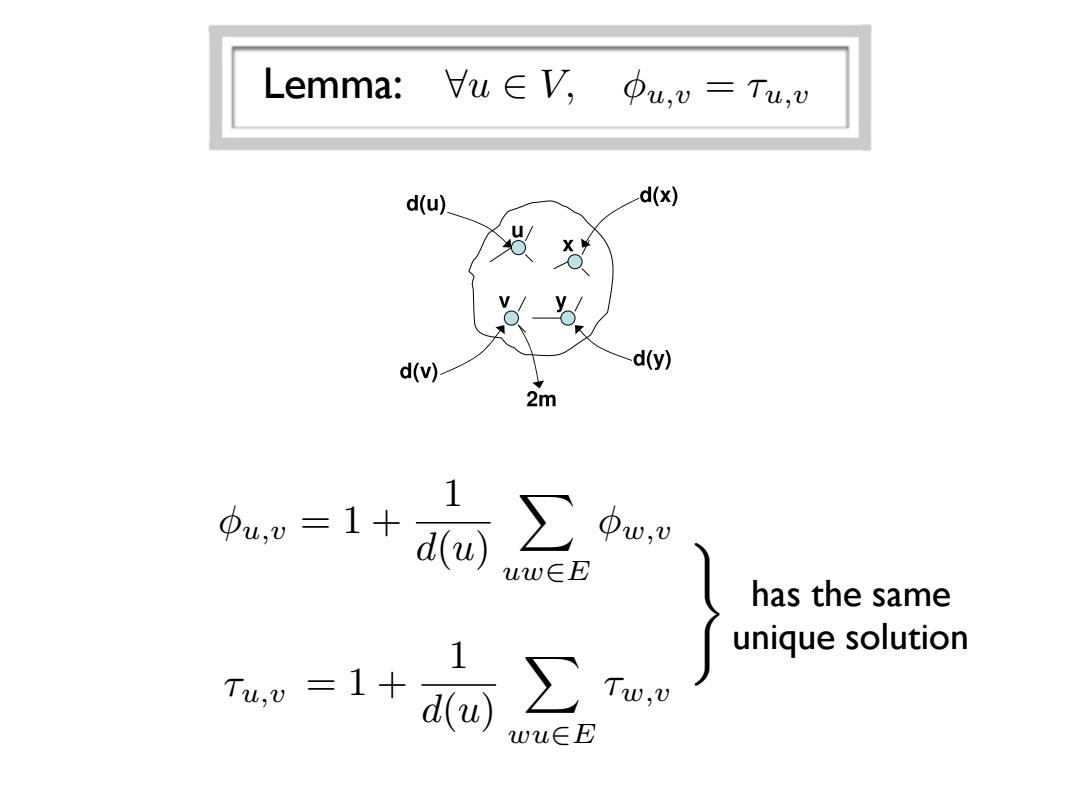
Lemma: u∈V,0u,v=Tu,u du)】 d(x) 袋效 d(v)- d(y) 2m Bw.v uw∈E has the same unique solution wu∈ELecture 23: November 17 23-3 Figure 23.1: Graph as an electrical network Definition 23.5 The e↵ective resistance R(u, v) between two nodes u and v is the potential di↵erence between u and v that is required to send one unit of current from u to v. Now we prove a few useful lemmas about hitting times. Consider first Scenario A, in which we inject d(x) units of current into each node x, and remove all 2m = P x d(x) units of current from node v, where d(x) denotes the degree of x. (See Figure 23.2.) Lemma 23.6 The potential di↵erence ￾u,v between v and any other node u in Scenario A satisfies ￾u,v = Hu,v. Figure 23.2: Scenario A Proof: Consider any vertex u 2 V . Using Kircho↵’s Laws and Ohm’s Law, we have d(u) = X (u,x)2E (current u ! x) (K1) = X (u,x)2E ￾u,x (Ohm) = X (u,x)2E (￾u,v ￾ ￾x,v) (K2) = d(u)￾u,v ￾ X (u,x)2E ￾x,v. Rearranging thus gives ￾u,v =1+ 1 d(u) X (u,x)2E ￾x,v. (23.1) On the other hand, consider the random walk starting from u. Thinking of just the first step of this walk, we see that the hitting time Hu,v satisfies Hu,v =1+ 1 d(u) X (u,x)2E Hx,v. But this is exactly the same system of linear equations as (23.1), satisfied by ￾u,v. Since we know that this system has a unique solution (the potentials are uniquely determined by the current flows), we deduce that Hu,v = ￾u,v 8u, v 2 V. Lemma: 8u 2 V, ￾u,v = ⌧u,v =1+ 1 d(u) X wu2E ⌧w,v ￾u,v =1+ 1 d(u) X uw2E ￾w,v ⌧u,v ) has the same unique solution