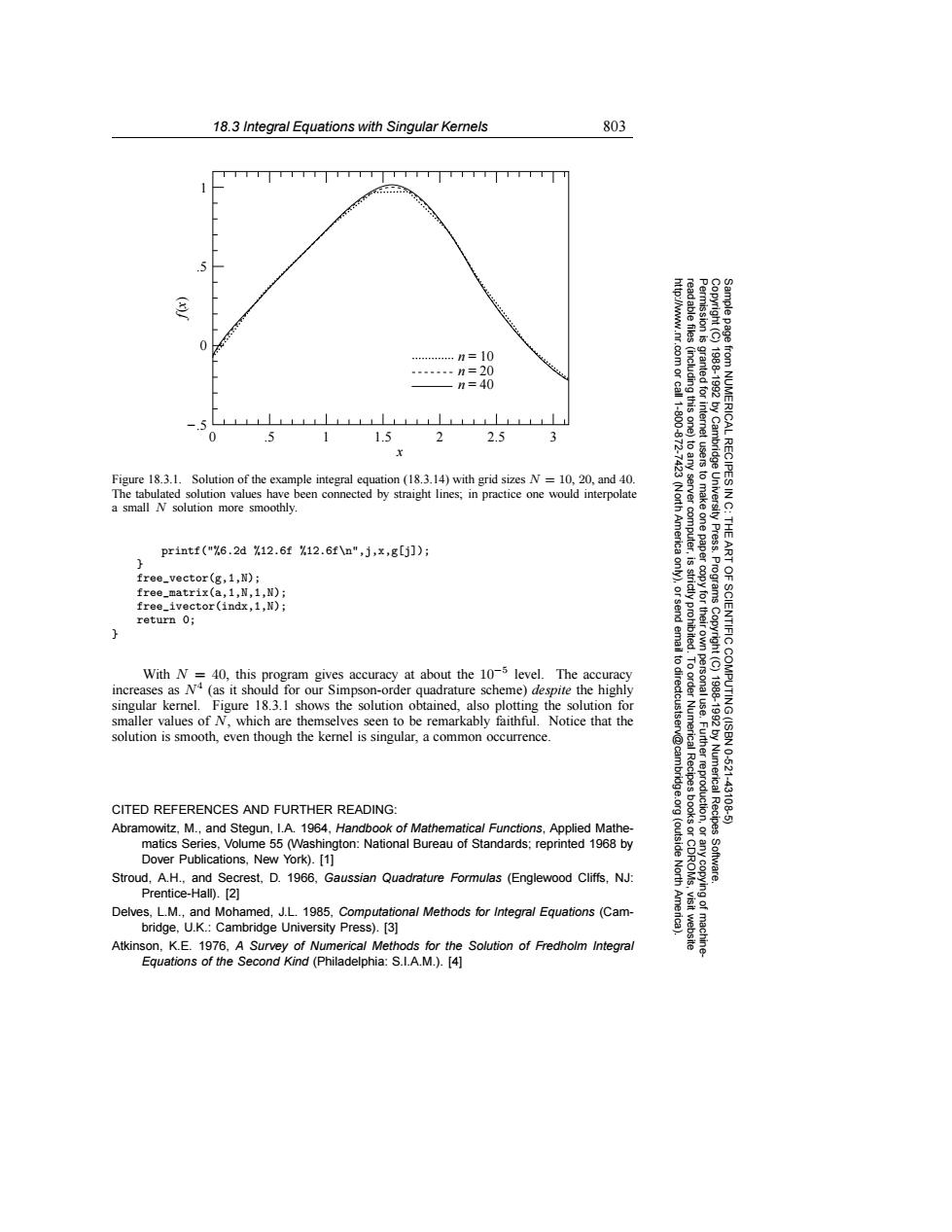
18.3 Integral Equations with Singular Kernels 803 TTTT http://www.nr Permission is read able files …n=10 -----n=20 -n=40 .com or call (including this one) granted fori 19881992 11-800 -.5 LLLL1LLLLLLLLLLLLLLLLLLLLLLLI 0 .5 1 1.5 2 2.5 3 Figure 18.3.1.Solution of the example integral equation(18.3.14)with grid sizes N=10,20,and 40. The tabulated solution values have been connected by straight lines;in practice one would interpolate to any server from NUMERICAL RECIPES IN C: a small N solution more smoothly. (North America Cambridge University Press. tusers to make one paper computer, THE printf("%6.2d%12.6f%12.6f\n",j,x,g[j]); 是 ART free_vector(g,1,N); free_matrix(a,1,N,1,N); st st Programs free_ivector(indx,1,N); return 0; With N=40,this program gives accuracy at about the 10-5 level.The accuracy to dir increases as N(as it should for our Simpson-order quadrature scheme)despite the highly singular kernel.Figure 18.3.1 shows the solution obtained,also plotting the solution for smaller values of N,which are themselves seen to be remarkably faithful.Notice that the 1788-1982 OF SCIENTIFIC COMPUTING(ISBN solution is smooth,even though the kernel is singular,a common occurrence. Further reproduction Numerical Recipes 10-621 CITED REFERENCES AND FURTHER READING: 43108 Abramowitz,M.,and Stegun,I.A.1964,Handbook of Mathematical Functions,Applied Mathe- matics Series,Volume 55 (Washington:National Bureau of Standards;reprinted 1968 by (outside Dover Publications,New York).[1] Stroud,A.H.,and Secrest,D.1966,Gaussian Quadrature Formulas (Englewood Cliffs,NJ: North Software. Prentice-Hall).[2] 6 Delves,L.M.,and Mohamed,J.L.1985,Computational Methods for Integral Equations (Cam- bridge.U.K.:Cambridge University Press).[3] Atkinson,K.E.1976.A Survey of Numerical Methods for the Solution of Fredholm Integral Equations of the Second Kind (Philadelphia:S.I.A.M.).[4]18.3 Integral Equations with Singular Kernels 803 Permission is granted for internet users to make one paper copy for their own personal use. Further reproduction, or any copyin Copyright (C) 1988-1992 by Cambridge University Press. Programs Copyright (C) 1988-1992 by Numerical Recipes Software. Sample page from NUMERICAL RECIPES IN C: THE ART OF SCIENTIFIC COMPUTING (ISBN 0-521-43108-5) g of machine￾readable files (including this one) to any server computer, is strictly prohibited. To order Numerical Recipes books or CDROMs, visit website http://www.nr.com or call 1-800-872-7423 (North America only), or send email to directcustserv@cambridge.org (outside North America). 0 .5 1 1.5 2 2.5 3 0 .5 1 −.5 f(x) x n = 10 n = 20 n = 40 Figure 18.3.1. Solution of the example integral equation (18.3.14) with grid sizes N = 10, 20, and 40. The tabulated solution values have been connected by straight lines; in practice one would interpolate a small N solution more smoothly. printf("%6.2d %12.6f %12.6f\n",j,x,g[j]); } free_vector(g,1,N); free_matrix(a,1,N,1,N); free_ivector(indx,1,N); return 0; } With N = 40, this program gives accuracy at about the 10−5 level. The accuracy increases as N4 (as it should for our Simpson-order quadrature scheme) despite the highly singular kernel. Figure 18.3.1 shows the solution obtained, also plotting the solution for smaller values of N, which are themselves seen to be remarkably faithful. Notice that the solution is smooth, even though the kernel is singular, a common occurrence. CITED REFERENCES AND FURTHER READING: Abramowitz, M., and Stegun, I.A. 1964, Handbook of Mathematical Functions, Applied Mathe￾matics Series, Volume 55 (Washington: National Bureau of Standards; reprinted 1968 by Dover Publications, New York). [1] Stroud, A.H., and Secrest, D. 1966, Gaussian Quadrature Formulas (Englewood Cliffs, NJ: Prentice-Hall). [2] Delves, L.M., and Mohamed, J.L. 1985, Computational Methods for Integral Equations (Cam￾bridge, U.K.: Cambridge University Press). [3] Atkinson, K.E. 1976, A Survey of Numerical Methods for the Solution of Fredholm Integral Equations of the Second Kind (Philadelphia: S.I.A.M.). [4]