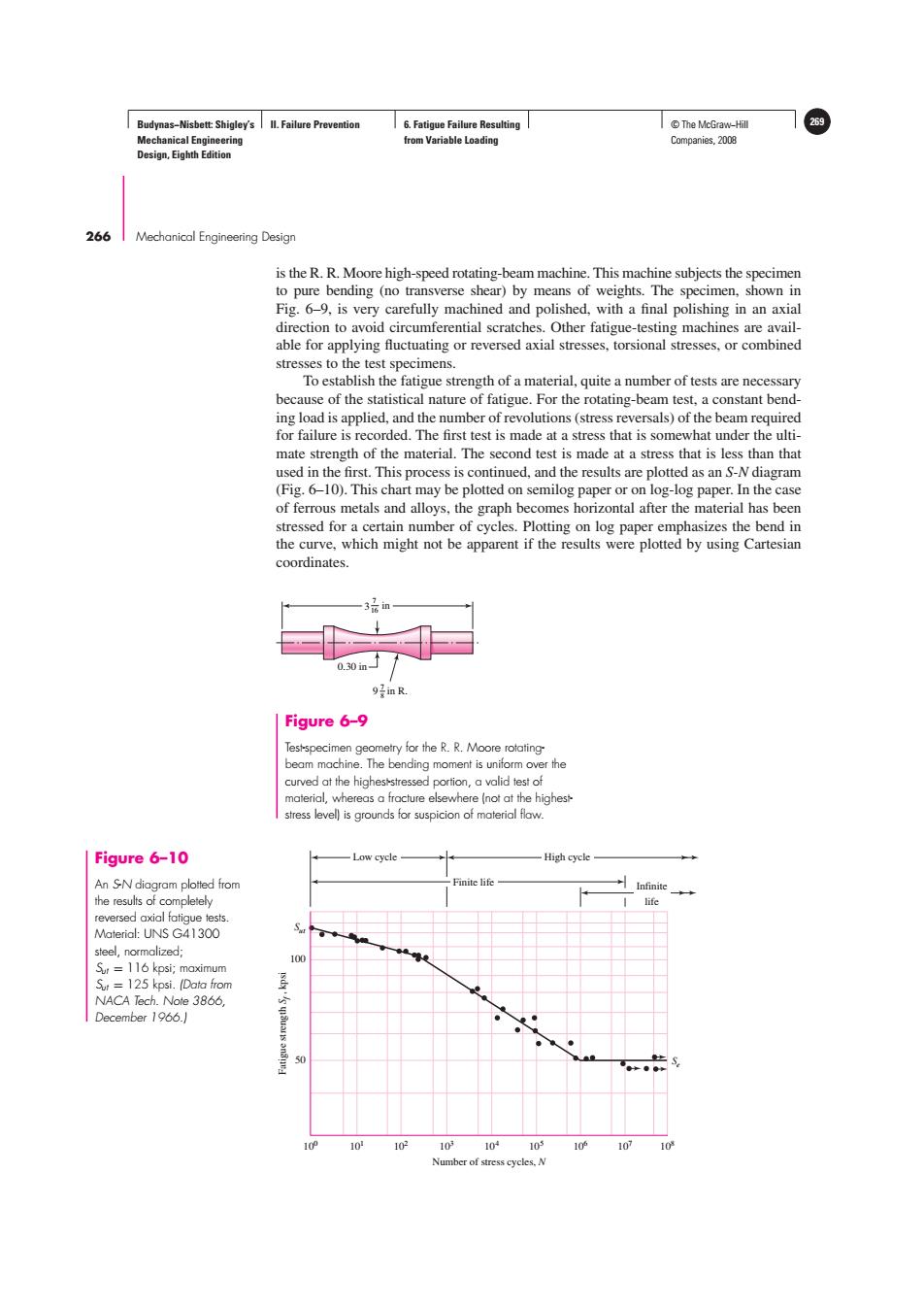
Budynas-Nisbett:Shigley's ll.Failure Prevention 6.Fatigue Failure Resulting ©The McGraw-Hil 269 Mechanical Engineering from Variable Loading Companies,2008 Design,Eighth Edition 266 Mechanical Engineering Design is the R.R.Moore high-speed rotating-beam machine.This machine subjects the specimen to pure bending (no transverse shear)by means of weights.The specimen,shown in Fig.6-9,is very carefully machined and polished,with a final polishing in an axial direction to avoid circumferential scratches.Other fatigue-testing machines are avail- able for applying fluctuating or reversed axial stresses,torsional stresses,or combined stresses to the test specimens. To establish the fatigue strength of a material,quite a number of tests are necessary because of the statistical nature of fatigue.For the rotating-beam test,a constant bend- ing load is applied,and the number of revolutions(stress reversals)of the beam required for failure is recorded.The first test is made at a stress that is somewhat under the ulti- mate strength of the material.The second test is made at a stress that is less than that used in the first.This process is continued,and the results are plotted as an S-N diagram (Fig.6-10).This chart may be plotted on semilog paper or on log-log paper.In the case of ferrous metals and alloys,the graph becomes horizontal after the material has been stressed for a certain number of cycles.Plotting on log paper emphasizes the bend in the curve,which might not be apparent if the results were plotted by using Cartesian coordinates. 3品n 0.30in 9in R. Figure 6-9 Test-specimen geometry for the R.R.Moore rotating beam machine.The bending moment is uniform over the curved at the higheststressed portion,a valid test of material,whereas a fracture elsewhere(not at the highes stress level)is grounds for suspicion of material flaw. Figure 6-10 -Low cycle .High cycle An SN diagram plotted from Finite life Infinite the results of completely life reversed axial fatigue tests. Material:UNS G41300 steel,normalized; 100 Sur =116 kpsi;maximum Sut =125 kpsi.(Data from NACA Tech.Note 3866, December 1966.] 50 10P 10 102 105 10105 10. 107 10 Number of stress cycles.NBudynas−Nisbett: Shigley’s Mechanical Engineering Design, Eighth Edition II. Failure Prevention 6. Fatigue Failure Resulting from Variable Loading © The McGraw−Hill 269 Companies, 2008 266 Mechanical Engineering Design 7 16 3 0.30 in in 9 in R. 7 8 Figure 6–9 Test-specimen geometry for the R. R. Moore rotating￾beam machine. The bending moment is uniform over the curved at the highest-stressed portion, a valid test of material, whereas a fracture elsewhere (not at the highest￾stress level) is grounds for suspicion of material flaw. 100 50 100 101 102 103 104 105 106 107 108 Number of stress cycles, N Se Sut Fatigue strength Sf , kpsi Low cycle High cycle Finite life Infinite life Figure 6–10 An S-N diagram plotted from the results of completely reversed axial fatigue tests. Material: UNS G41300 steel, normalized; Sut = 116 kpsi; maximum Sut = 125 kpsi. (Data from NACA Tech. Note 3866, December 1966.) is the R. R. Moore high-speed rotating-beam machine. This machine subjects the specimen to pure bending (no transverse shear) by means of weights. The specimen, shown in Fig. 6–9, is very carefully machined and polished, with a final polishing in an axial direction to avoid circumferential scratches. Other fatigue-testing machines are avail￾able for applying fluctuating or reversed axial stresses, torsional stresses, or combined stresses to the test specimens. To establish the fatigue strength of a material, quite a number of tests are necessary because of the statistical nature of fatigue. For the rotating-beam test, a constant bend￾ing load is applied, and the number of revolutions (stress reversals) of the beam required for failure is recorded. The first test is made at a stress that is somewhat under the ulti￾mate strength of the material. The second test is made at a stress that is less than that used in the first. This process is continued, and the results are plotted as an S-N diagram (Fig. 6–10). This chart may be plotted on semilog paper or on log-log paper. In the case of ferrous metals and alloys, the graph becomes horizontal after the material has been stressed for a certain number of cycles. Plotting on log paper emphasizes the bend in the curve, which might not be apparent if the results were plotted by using Cartesian coordinates