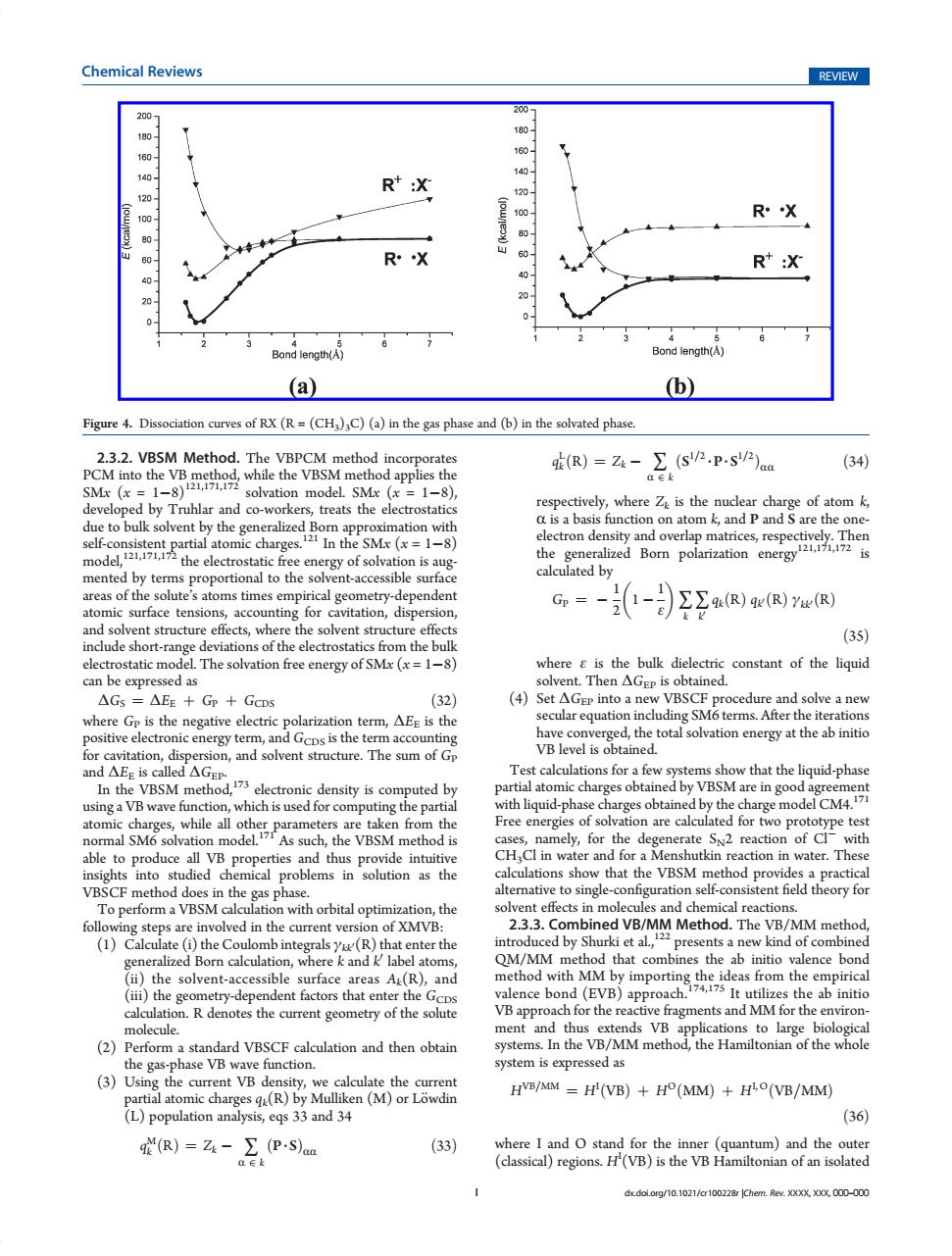
Chemical Reviews REVIEW 200 2007 180 180 160 1e0 140 140 R+:X 120 120 100 100 R·X 80- ◆ 60 RX R*:X 40 20 0 Bond length(A) Bond length(A) (a) (b) Figure 4.Dissociation curves of RX(R=(CH3)3C)(a)in the gas phase and(b)in the solvated phase. 2.3.2.VBSM Method.The VBPCM method incorporates qi(R)=Zk- (Sp.p-s/P)aa (34) PCM into the VB method,while the VBSM method applies the a∈k SMx(x=1-8)2L,171,172 solvation model.SMx (x=1-8), developed by Truhlar and co-workers,treats the electrostatics respectively,where Zk is the nuclear charge of atom k, due to bulk solvent by the generalized Born approximation with a is a basis function on atom k,and P and S are the one- self-consistent partial atomic charges.21 In the SMx(=1-8) electron density and overlap matrices,respectively.Then modelthe electrostatic ree energy of soation isaug the generalized Born polarization energy 21,171,172is mented by terms proportional to the solvent-accessible surface calculated by areas of the solute's atoms times empirical geometry-dependent 1-司9R)9R)R) 1 Gp = atomic surface tensions,accounting for cavitation,dispersion, and solvent structure effects,where the solvent structure effects (35) include short-range deviations of the electrostatics from the bulk electrostatic model.The solvation free energy of SMx(x=1-8) where E is the bulk dielectric constant of the liquid can be expressed as solvent.Then AGep is obtained. △Gs=△EE+Gn+GCDs (32) (4)Set AGEp into a new VBSCF procedure and solve a new where Gp is the negative electric polarization term,AEE is the secular equation including SM6 terms.After the iterations positive electronic energy term,and Gcps is the term accounting have converged,the total solvation energy at the ab initio for cavitation,dispersion,and solvent structure.The sum of Gp VB level is obtained. and△Ee is called△Gep Test calculations for a few systems show that the liquid-phase In the VBSM method,173 electronic density is computed by partial atomic charges obtained by VBSM are in good agreement using a VB wave function,which is used for computing the partial with liquid-phase charges obtained by the charge mode CM atomic charges,while all other parameters are taken from the Free energies of solvation are calculated for two prototype test normal SM6 solvation model.71 As such,the VBSM method is cases,namely,for the degenerate Sv2 reaction of Cl with able to produce all VB properties and thus provide intuitive CH3Cl in water and for a Menshutkin reaction in water.These insights into studied chemical problems in solution as the calculations show that the VBSM method provides a practical VBSCF method does in the gas phase. alternative to single-configuration self-consistent field theory for To perform a VBSM calculation with orbital optimization,the solvent effects in molecules and chemical reactions following steps are involved in the current version of XMVB: 2.3.3.Combined VB/MM Method.The VB/MM method, (1)Calculate (i)the Coulomb integrals yu(R)that enter the introduced by Shurki et al,presents a new kind of combined generalized Born calculation,where k and k label atoms, QM/MM method that combines the ab initio valence bond (ii)the solvent-accessible surface areas Ak(R),and method with MM by importing the ideas from the empirical (iii)the geometry-dependent factors that enter the Gcps valence bond (EVB)approach.74175 It utilizes the ab initio calculation.R denotes the current geometry of the solute VB approach for the reactive fragments and MM for the environ- molecule. ment and thus extends VB applications to large biological (2)Perform a standard VBSCF calculation and then obtain systems.In the VB/MM method,the Hamiltonian of the whole the gas-phase VB wave function. system is expressed as (3)Using the current VB density,we calculate the current partial atomic charges qu(R)by Mulliken (M)or Lowdin HVB/MIM =H'(VB)+HO(MM)+H(VB/MM) (L)population analysis,eqs 33 and 34 (36) q(R)=Zk-∑(PS)aa (33) where I and O stand for the inner (quantum)and the outer a∈k (classical)regions.H(VB)is the VB Hamiltonian of an isolated dx.dol.org/10.1021/cr100228r Chem.Rev.XXXX,XXX,000-000I dx.doi.org/10.1021/cr100228r |Chem. Rev. XXXX, XXX, 000–000 Chemical Reviews REVIEW 2.3.2. VBSM Method. The VBPCM method incorporates PCM into the VB method, while the VBSM method applies the SMx (x = 1
8)121,171,172 solvation model. SMx (x = 1
8), developed by Truhlar and co-workers, treats the electrostatics due to bulk solvent by the generalized Born approximation with self-consistent partial atomic charges.121 In the SMx (x = 1
8) model,121,171,172 the electrostatic free energy of solvation is aug￾mented by terms proportional to the solvent-accessible surface areas of the solute’s atoms times empirical geometry-dependent atomic surface tensions, accounting for cavitation, dispersion, and solvent structure effects, where the solvent structure effects include short-range deviations of the electrostatics from the bulk electrostatic model. The solvation free energy of SMx (x = 1
8) can be expressed as ΔGS ¼ ΔEE þ GP þ GCDS ð32Þ where GP is the negative electric polarization term, ΔEE is the positive electronic energy term, and GCDS is the term accounting for cavitation, dispersion, and solvent structure. The sum of GP and ΔEE is called ΔGEP. In the VBSM method,173 electronic density is computed by using a VB wave function, which is used for computing the partial atomic charges, while all other parameters are taken from the normal SM6 solvation model.171 As such, the VBSM method is able to produce all VB properties and thus provide intuitive insights into studied chemical problems in solution as the VBSCF method does in the gas phase. To perform a VBSM calculation with orbital optimization, the following steps are involved in the current version of XMVB: (1) Calculate (i) the Coulomb integrals γkk0(R) that enter the generalized Born calculation, where k and k0 label atoms, (ii) the solvent-accessible surface areas Ak(R), and (iii) the geometry-dependent factors that enter the GCDS calculation. R denotes the current geometry of the solute molecule. (2) Perform a standard VBSCF calculation and then obtain the gas-phase VB wave function. (3) Using the current VB density, we calculate the current partial atomic charges qk(R) by Mulliken (M) or L€owdin (L) population analysis, eqs 33 and 34 qM k ðRÞ ¼ Zk
∑ R ∈ k ðP 3 SÞRR ð33Þ qL k ðRÞ ¼ Zk
∑ R ∈ k ðS1=2 3 P 3 S1=2 ÞRR ð34Þ respectively, where Zk is the nuclear charge of atom k, R is a basis function on atom k, and P and S are the one￾electron density and overlap matrices, respectively. Then the generalized Born polarization energy121,171,172 is calculated by GP ¼
1 2 1
1 ε
∑ k ∑ k0 qkðRÞ qk0ðRÞ γkk0ðRÞ ð35Þ where ε is the bulk dielectric constant of the liquid solvent. Then ΔGEP is obtained. (4) Set ΔGEP into a new VBSCF procedure and solve a new secular equation including SM6 terms. After the iterations have converged, the total solvation energy at the ab initio VB level is obtained. Test calculations for a few systems show that the liquid-phase partial atomic charges obtained by VBSM are in good agreement with liquid-phase charges obtained by the charge model CM4.171 Free energies of solvation are calculated for two prototype test cases, namely, for the degenerate SN2 reaction of Cl
with CH3Cl in water and for a Menshutkin reaction in water. These calculations show that the VBSM method provides a practical alternative to single-configuration self-consistent field theory for solvent effects in molecules and chemical reactions. 2.3.3. Combined VB/MM Method. The VB/MM method, introduced by Shurki et al.,122 presents a new kind of combined QM/MM method that combines the ab initio valence bond method with MM by importing the ideas from the empirical valence bond (EVB) approach.174,175 It utilizes the ab initio VB approach for the reactive fragments and MM for the environ￾ment and thus extends VB applications to large biological systems. In the VB/MM method, the Hamiltonian of the whole system is expressed as HVB=MM ¼ HI ðVBÞ þ HOðMMÞ þ HI, OðVB=MMÞ ð36Þ where I and O stand for the inner (quantum) and the outer (classical) regions. HI (VB) is the VB Hamiltonian of an isolated Figure 4. Dissociation curves of RX (R = (CH3)3C) (a) in the gas phase and (b) in the solvated phase.