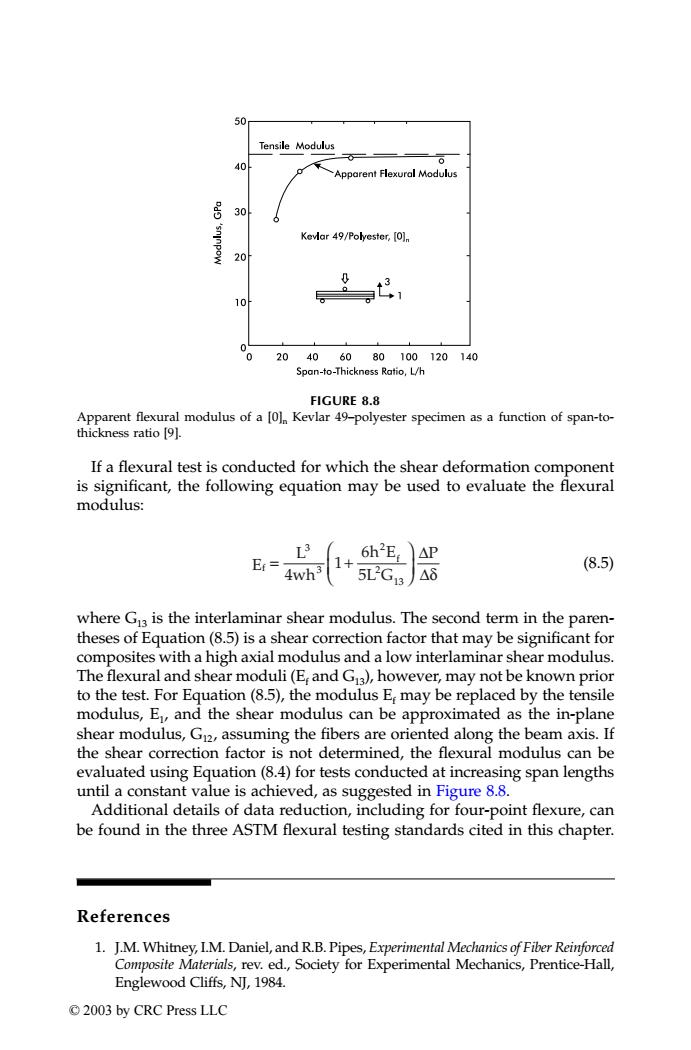
50 Tensile Modulus 40 Apparent Flexural Modulus 30 Kevar 49/Polyester,[O] 20 0 10 00 20406080100120140 Span-to-Thickness Ratio,L/h FIGURE 8.8 Apparent flexural modulus of a [Ol Kevlar 49-polyester specimen as a function of span-to- thickness ratio [9]. If a flexural test is conducted for which the shear deformation component is significant,the following equation may be used to evaluate the flexural modulus: L3 Er= 6h2EAP 4wh3 5LGIA8 (8.5) where Gs is the interlaminar shear modulus.The second term in the paren- theses of Equation(8.5)is a shear correction factor that may be significant for composites with a high axial modulus and a low interlaminar shear modulus. The flexural and shear moduli(E and G3),however,may not be known prior to the test.For Equation(8.5),the modulus E may be replaced by the tensile modulus,E,and the shear modulus can be approximated as the in-plane shear modulus,G2,assuming the fibers are oriented along the beam axis.If the shear correction factor is not determined,the flexural modulus can be evaluated using Equation(8.4)for tests conducted at increasing span lengths until a constant value is achieved,as suggested in Figure 8.8. Additional details of data reduction,including for four-point flexure,can be found in the three ASTM flexural testing standards cited in this chapter. References 1.J.M.Whitney,I.M.Daniel,and R.B.Pipes,Experimental Mechanics of Fiber Reinforced Composite Materials,rev.ed.,Society for Experimental Mechanics,Prentice-Hall, Englewood Cliffs,NJ,1984. ©2003 by CRC Press LLCIf a flexural test is conducted for which the shear deformation component is significant, the following equation may be used to evaluate the flexural modulus: (8.5) where G13 is the interlaminar shear modulus. The second term in the paren￾theses of Equation (8.5) is a shear correction factor that may be significant for composites with a high axial modulus and a low interlaminar shear modulus. The flexural and shear moduli (Ef and G13), however, may not be known prior to the test. For Equation (8.5), the modulus Ef may be replaced by the tensile modulus, E1, and the shear modulus can be approximated as the in-plane shear modulus, G12, assuming the fibers are oriented along the beam axis. If the shear correction factor is not determined, the flexural modulus can be evaluated using Equation (8.4) for tests conducted at increasing span lengths until a constant value is achieved, as suggested in Figure 8.8. Additional details of data reduction, including for four-point flexure, can be found in the three ASTM flexural testing standards cited in this chapter. References 1. J.M. Whitney, I.M. Daniel, and R.B. Pipes, Experimental Mechanics of Fiber Reinforced Composite Materials, rev. ed., Society for Experimental Mechanics, Prentice-Hall, Englewood Cliffs, NJ, 1984. FIGURE 8.8 Apparent flexural modulus of a [0]n Kevlar 49–polyester specimen as a function of span-to￾thickness ratio [9]. f f E L 4wh 1 h E L G P = +       3 3 2 2 13 6 5 ∆ ∆δ TX001_ch08_Frame Page 129 Saturday, September 21, 2002 4:59 AM © 2003 by CRC Press LLC