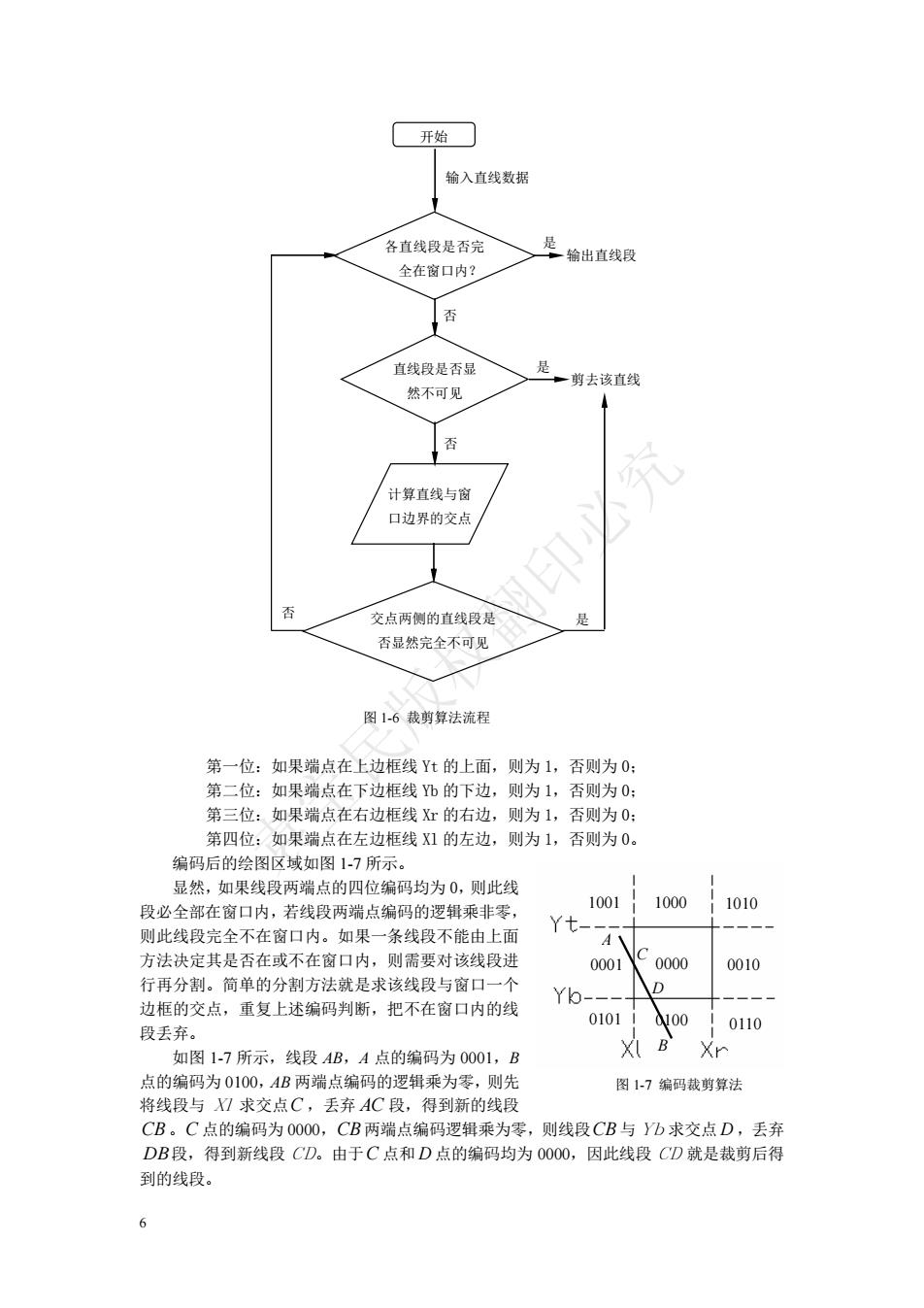
开始 输入直线数据 各直线段是否完 全在窗口内？ 是输出直线段 1否 直线段是否显 是 一剪去该直线 然不可见 计算直线与窗 口边界的交 交点两侧的直线段是 是 否显然完全不可见 图1-6裁剪算法流程 第一位：如果端点在上边框线Yt的上面，则为1，否则为0： 第二位：如果端点在下边框线b的下边，则为1，否则为0： 第三位：如果端点在右边框线X江的右边，则为1，否则为0： 第四位：如果端点在左边框线Ⅺ的左边，则为1，否则为0 编码后的绘图区域如图17所示。 显然，如果线段两端点的四位编码均为0，则此线 段必全部在窗口内，若线段两端点编码的逻辑乘非零， 1001 1000 1010 则此线段完全不在窗口内。如果一条线段不能由上面 Yt A 方法决定其是否在或不在窗口内 则需要 线段 0001 0000 0010 行再分制。简单的分割方法就是求该线段与窗口一个 边框的交点，重复上述编码判断，把不在窗口内的线 Yb. 0101 段丢弃。 V00 0110 加图17所示，线段AB,A点的码为0001，B Xr 图1-7编码裁剪算法 CB。C点的编码为00OO,CB两端点编码逻辑乘为零，则线段CB与Yb求交点D,丢弃 DB段，得到新线段CD。由于C点和D点的编码均为O0O0,因此线段CD就是裁剪后得 到的线段。 66 图 1-6 裁剪算法流程 第一位：如果端点在上边框线 Yt 的上面，则为 1，否则为 0； 第二位：如果端点在下边框线 Yb 的下边，则为 1，否则为 0； 第三位：如果端点在右边框线 Xr 的右边，则为 1，否则为 0； 第四位：如果端点在左边框线 Xl 的左边，则为 1，否则为 0。 编码后的绘图区域如图 1-7 所示。 显然，如果线段两端点的四位编码均为 0，则此线 段必全部在窗口内，若线段两端点编码的逻辑乘非零， 则此线段完全不在窗口内。如果一条线段不能由上面 方法决定其是否在或不在窗口内，则需要对该线段进 行再分割。简单的分割方法就是求该线段与窗口一个 边框的交点，重复上述编码判断，把不在窗口内的线 段丢弃。 如图 1-7 所示，线段 AB，A 点的编码为 0001，B 点的编码为 0100，AB 两端点编码的逻辑乘为零，则先 将线段与 Xl 求交点 C ，丢弃 AC 段，得到新的线段 CB 。C 点的编码为 0000，CB 两端点编码逻辑乘为零，则线段 CB 与 Yb 求交点 D ，丢弃 DB 段，得到新线段 CD。由于 C 点和 D 点的编码均为 0000，因此线段 CD 就是裁剪后得 到的线段。 开始 输入直线数据 各直线段是否完 全在窗口内？ 输出直线段 是 否 直线段是否显 然不可见 是 剪去该直线 否 计算直线与窗 口边界的交点 交点两侧的直线段是 否显然完全不可见 否 是 1010 0010 0110 1000 0000 0100 1001 0001 0101 B C D 图 图 1-7 编码裁剪算法 A 袁宝民版权翻印必究