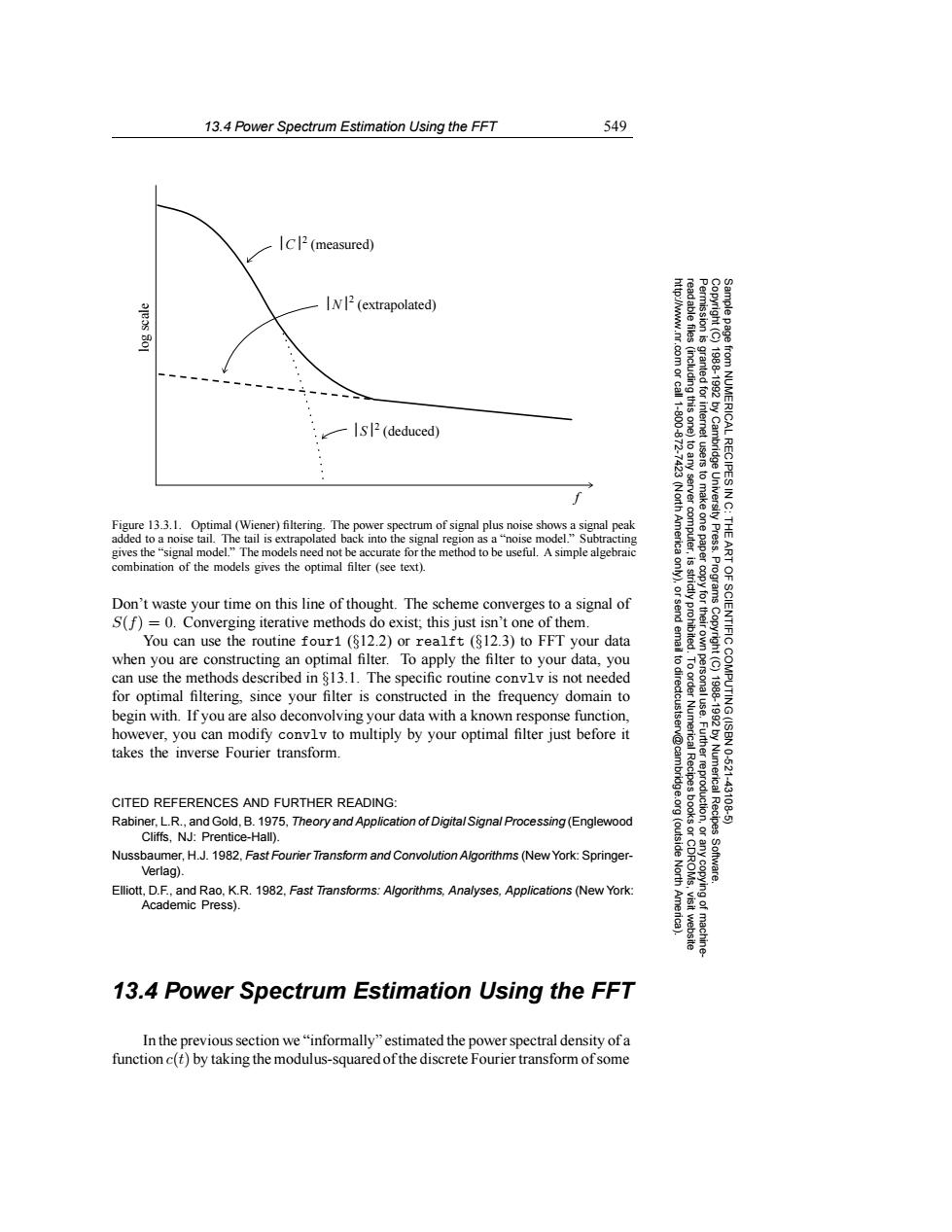
13.4 Power Spectrum Estimation Using the FFT 549 IC2(measured) IN2(extrapolated) http://www.nr.com or call 1-800-872- Permission is read able files (including this one) granted fori IS2(deduced) internet from NUMERICAL RECIPES IN C: (North Figure 13.3.1.Optimal (Wiener)filtering.The power spectrum of signal plus noise shows a signal peak added to a noise tail.The tail is extrapolated back into the signal region as a"noise model."Subtracting America tusers to make one paper 1988-1992 by Cambridge University Press. THE gives the"signal model."The models need not be accurate for the method to be useful.A simple algebraic 是 ART combination of the models gives the optimal filter (see text). Programs Don't waste your time on this line of thought.The scheme converges to a signal of ictly proh S(f)=0.Converging iterative methods do exist;this just isn't one of them You can use the routine four1 (812.2)or realft (812.3)to FFT your data when you are constructing an optimal filter.To apply the filter to your data,you can use the methods described in $13.1.The specific routine convlv is not needed for optimal filtering,since your filter is constructed in the frequency domain to begin with.If you are also deconvolving your data with a known response function, 1988-1992 however,you can modify convlv to multiply by your optimal filter just before it OF SCIENTIFIC COMPUTING(ISBN 0-521- takes the inverse Fourier transform. CITED REFERENCES AND FURTHER READING: Numerical Recipes -43108-5 Rabiner,L.R.,and Gold,B.1975,Theory and Application of Digital Signal Processing(Englewood Cliffs,NJ:Prentice-Hall). (outside Nussbaumer,H.J.1982,Fast Fourier Transform and Convolution Algorithms(New York:Springer- Verlag). North Software. Elliott,D.F.,and Rao.K.R.1982.Fast Transforms:Algorithms,Analyses,Applications (New York: Academic Press). visit website machine 13.4 Power Spectrum Estimation Using the FFT In the previous section we"informally"estimated the power spectral density ofa function c(t)by taking the modulus-squared of the discrete Fourier transform of some13.4 Power Spectrum Estimation Using the FFT 549 Permission is granted for internet users to make one paper copy for their own personal use. Further reproduction, or any copyin Copyright (C) 1988-1992 by Cambridge University Press. Programs Copyright (C) 1988-1992 by Numerical Recipes Software. Sample page from NUMERICAL RECIPES IN C: THE ART OF SCIENTIFIC COMPUTING (ISBN 0-521-43108-5) g of machine￾readable files (including this one) to any server computer, is strictly prohibited. To order Numerical Recipes books or CDROMs, visit website http://www.nr.com or call 1-800-872-7423 (North America only), or send email to directcustserv@cambridge.org (outside North America).  S 2 (deduced)  N 2 (extrapolated)  C 2 (measured) log scale f Figure 13.3.1. Optimal (Wiener) filtering. The power spectrum of signal plus noise shows a signal peak added to a noise tail. The tail is extrapolated back into the signal region as a “noise model.” Subtracting gives the “signal model.” The models need not be accurate for the method to be useful. A simple algebraic combination of the models gives the optimal filter (see text). Don’t waste your time on this line of thought. The scheme converges to a signal of S(f)=0. Converging iterative methods do exist; this just isn’t one of them. You can use the routine four1 (§12.2) or realft (§12.3) to FFT your data when you are constructing an optimal filter. To apply the filter to your data, you can use the methods described in §13.1. The specific routine convlv is not needed for optimal filtering, since your filter is constructed in the frequency domain to begin with. If you are also deconvolving your data with a known response function, however, you can modify convlv to multiply by your optimal filter just before it takes the inverse Fourier transform. CITED REFERENCES AND FURTHER READING: Rabiner, L.R., and Gold, B. 1975, Theory and Application of Digital Signal Processing (Englewood Cliffs, NJ: Prentice-Hall). Nussbaumer, H.J. 1982, Fast Fourier Transform and Convolution Algorithms (New York: Springer￾Verlag). Elliott, D.F., and Rao, K.R. 1982, Fast Transforms: Algorithms, Analyses, Applications (New York: Academic Press). 13.4 Power Spectrum Estimation Using the FFT In the previous section we “informally” estimated the power spectral density of a function c(t) by taking the modulus-squared of the discrete Fourier transform of some