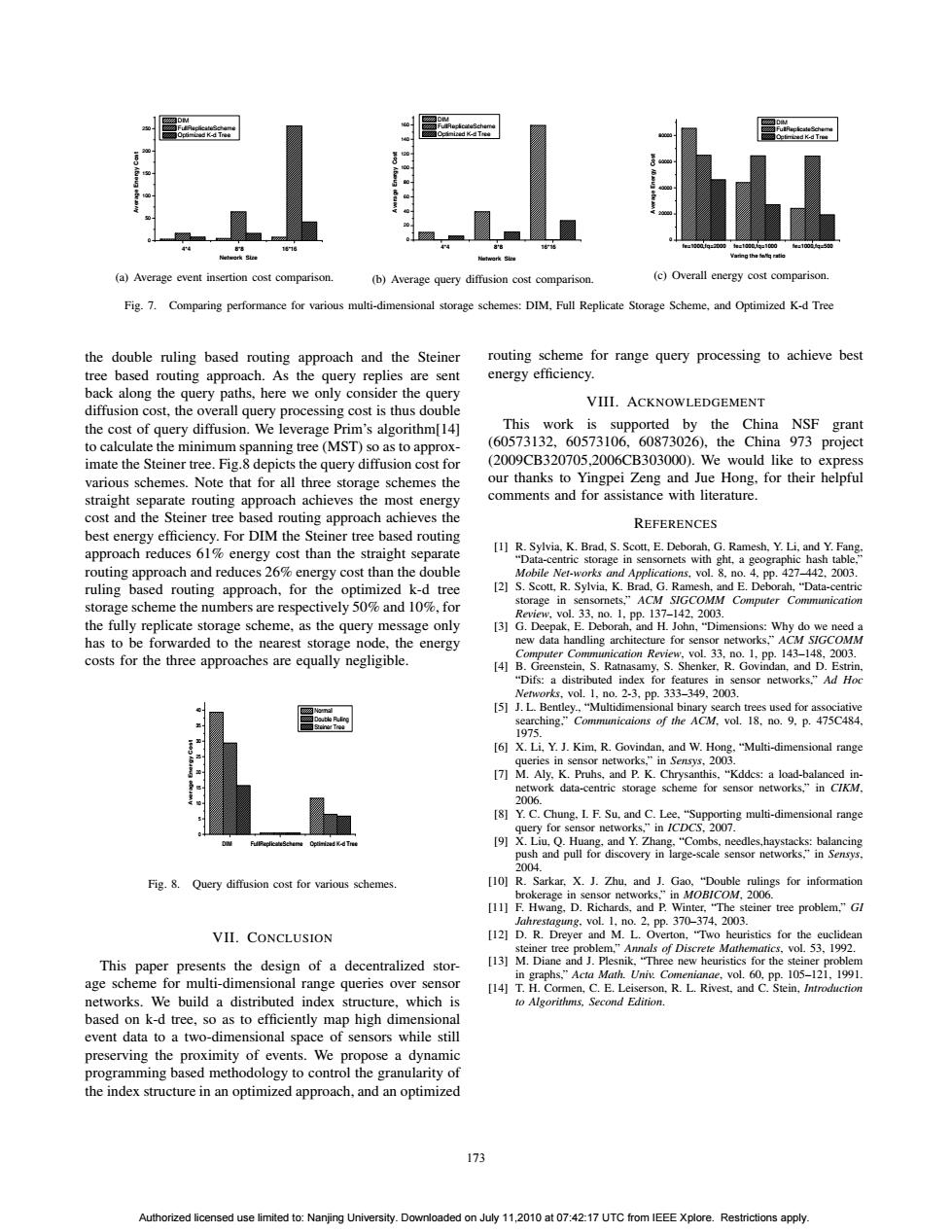
Kd Te 44 88 =100 agha向 (a)Average event insertion cost comparison. (b)Average query diffusion cost comparison. (c)Overall energy cost comparison. Fig.7.Comparing performance for various multi-dimensional storage schemes:DIM,Full Replicate Storage Scheme,and Optimized K-d Tree the double ruling based routing approach and the Steiner routing scheme for range query processing to achieve best tree based routing approach.As the query replies are sent energy efficiency. back along the query paths,here we only consider the query VIII.ACKNOWLEDGEMENT diffusion cost,the overall query processing cost is thus double the cost of query diffusion.We leverage Prim's algorithm[14] This work is supported by the China NSF grant to calculate the minimum spanning tree(MST)so as to approx- (60573132,60573106,60873026),the China973 project imate the Steiner tree.Fig.8 depicts the query diffusion cost for (2009CB320705,2006CB303000).We would like to express various schemes.Note that for all three storage schemes the our thanks to Yingpei Zeng and Jue Hong,for their helpful straight separate routing approach achieves the most energy comments and for assistance with literature. cost and the Steiner tree based routing approach achieves the REFERENCES best energy efficiency.For DIM the Steiner tree based routing approach reduces 61%energy cost than the straight separate [1]R.Sylvia,K.Brad,S.Scott,E.Deborah.G.Ramesh,Y.Li,and Y.Fang. "Data-centric storage in sensomets with ght,a geographic hash table, routing approach and reduces 26%energy cost than the double Mobile Net-works and Applications.vol.8.no.4.pp.427-442.2003. ruling based routing approach,for the optimized k-d tree [2]S.Scott,R.Sylvia,K.Brad,G.Ramesh,and E.Deborah,"Data-centric storage scheme the numbers are respectively 50%and 10%,for storage in sensornets,"ACM SIGCOMM Computer Communication Review,vol.33,no.1,pp.137-142,2003. the fully replicate storage scheme,as the query message only [3]G.Deepak.E.Deborah,and H.John,"Dimensions:Why do we need a has to be forwarded to the nearest storage node,the energy new data handling architecture for sensor networks,"ACM SIGCOMM costs for the three approaches are equally negligible. Computer Communication Review,vol.33.no.1,pp.143-148.2003. [4]B.Greenstein,S.Ratnasamy,S.Shenker.R.Govindan,and D.Estrin, "Difs:a distributed index for features in sensor networks,"Ad Hoc Networks,.vol.1,no.2-3,Pp.333-349,2003. [5]J.L.Bentley.,"Multidimensional binary search trees used for associative searching."Communicaions of the ACM,vol.18.no.9.p.475C484 1975. [6]X.Li,Y.J.Kim,R.Govindan,and W.Hong,"Multi-dimensional range queries in sensor networks,"in Sensys,2003. [7]M.Aly.K.Pruhs,and P.K.Chrysanthis."Kddcs:a load-balanced in- network data-centric storage scheme for sensor networks,"in CIKM. 2006. [8]Y.C.Chung.I.F.Su,and C.Lee,"Supporting multi-dimensional range query for sensor networks."in ICDCS.2007. D [9]X.Liu,Q.Huang.and Y.Zhang."Combs,needles,haystacks:balancing push and pull for discovery in large-scale sensor networks,"in Sensys. 2004. Fig.8.Query diffusion cost for various schemes. [10]R.Sarkar,X.J.Zhu,and J.Gao,"Double rulings for information brokerage in sensor networks,"in MOB/COM,2006. [11]F.Hwang.D.Richards,and P.Winter."The steiner tree problem,"G Jahrestagung.vol.1.no.2.pp.370-374,2003. VII.CONCLUSION [12]D.R.Dreyer and M.L.Overton,"Two heuristics for the euclidean steiner tree problem,"Annals of Discrete Mathematics,vol.53,1992. This paper presents the design of a decentralized stor- [13]M.Diane and J.Plesnik,"Three new heuristics for the steiner problem age scheme for multi-dimensional range queries over sensor in graphs,"Acta Math.Univ:Comenianae,vol.60,pp.105-121,1991. [14]T.H.Cormen,C.E.Leiserson,R.L.Rivest,and C. Stein,Introduction networks.We build a distributed index structure,which is to Algorithms,Second Edition. based on k-d tree,so as to efficiently map high dimensional event data to a two-dimensional space of sensors while still preserving the proximity of events.We propose a dynamic programming based methodology to control the granularity of the index structure in an optimized approach,and an optimized 173 Authorized licensed use limited to:Nanjing University.Downloaded on July 11,2010 at 07:42:17 UTC from IEEE Xplore.Restrictions apply.0 50 100 150 200 250 4*4 8*8 16*16 Average Energy Cost Network Size DIM FullReplicateScheme Optimized K-d Tree (a) Average event insertion cost comparison. 0 20 40 60 80 100 120 140 160 4*4 8*8 16*16 Average Energy Cost Network Size DIM FullReplicateScheme Optimized K-d Tree (b) Average query diffusion cost comparison. 0 20000 40000 60000 80000 DIM FullReplicateScheme Optimized K-d Tree fe=1000,fq=2000 fe=1000,fq=1000 fe=1000,fq=500 Average Energy Cost Varing the fe/fq ratio (c) Overall energy cost comparison. Fig. 7. Comparing performance for various multi-dimensional storage schemes: DIM, Full Replicate Storage Scheme, and Optimized K-d Tree the double ruling based routing approach and the Steiner tree based routing approach. As the query replies are sent back along the query paths, here we only consider the query diffusion cost, the overall query processing cost is thus double the cost of query diffusion. We leverage Prim’s algorithm[14] to calculate the minimum spanning tree (MST) so as to approx￾imate the Steiner tree. Fig.8 depicts the query diffusion cost for various schemes. Note that for all three storage schemes the straight separate routing approach achieves the most energy cost and the Steiner tree based routing approach achieves the best energy efficiency. For DIM the Steiner tree based routing approach reduces 61% energy cost than the straight separate routing approach and reduces 26% energy cost than the double ruling based routing approach, for the optimized k-d tree storage scheme the numbers are respectively 50% and 10%, for the fully replicate storage scheme, as the query message only has to be forwarded to the nearest storage node, the energy costs for the three approaches are equally negligible. 0 5 10 15 20 25 30 35 40 DIM FullReplicateScheme Optimized K-d Tree Normal Double Ruling Steiner Tree Average Energy Cost Fig. 8. Query diffusion cost for various schemes. VII. CONCLUSION This paper presents the design of a decentralized stor￾age scheme for multi-dimensional range queries over sensor networks. We build a distributed index structure, which is based on k-d tree, so as to efficiently map high dimensional event data to a two-dimensional space of sensors while still preserving the proximity of events. We propose a dynamic programming based methodology to control the granularity of the index structure in an optimized approach, and an optimized routing scheme for range query processing to achieve best energy efficiency. VIII. ACKNOWLEDGEMENT This work is supported by the China NSF grant (60573132, 60573106, 60873026), the China 973 project (2009CB320705,2006CB303000). We would like to express our thanks to Yingpei Zeng and Jue Hong, for their helpful comments and for assistance with literature. REFERENCES [1] R. Sylvia, K. Brad, S. Scott, E. Deborah, G. Ramesh, Y. Li, and Y. Fang, “Data-centric storage in sensornets with ght, a geographic hash table,” Mobile Net-works and Applications, vol. 8, no. 4, pp. 427–442, 2003. [2] S. Scott, R. Sylvia, K. Brad, G. Ramesh, and E. Deborah, “Data-centric storage in sensornets,” ACM SIGCOMM Computer Communication Review, vol. 33, no. 1, pp. 137–142, 2003. [3] G. Deepak, E. Deborah, and H. John, “Dimensions: Why do we need a new data handling architecture for sensor networks,” ACM SIGCOMM Computer Communication Review, vol. 33, no. 1, pp. 143–148, 2003. [4] B. Greenstein, S. Ratnasamy, S. Shenker, R. Govindan, and D. Estrin, “Difs: a distributed index for features in sensor networks,” Ad Hoc Networks, vol. 1, no. 2-3, pp. 333–349, 2003. [5] J. L. Bentley., “Multidimensional binary search trees used for associative searching,” Communicaions of the ACM, vol. 18, no. 9, p. 475C484, 1975. [6] X. Li, Y. J. Kim, R. Govindan, and W. Hong, “Multi-dimensional range queries in sensor networks,” in Sensys, 2003. [7] M. Aly, K. Pruhs, and P. K. Chrysanthis, “Kddcs: a load-balanced in￾network data-centric storage scheme for sensor networks,” in CIKM, 2006. [8] Y. C. Chung, I. F. Su, and C. Lee, “Supporting multi-dimensional range query for sensor networks,” in ICDCS, 2007. [9] X. Liu, Q. Huang, and Y. Zhang, “Combs, needles,haystacks: balancing push and pull for discovery in large-scale sensor networks,” in Sensys, 2004. [10] R. Sarkar, X. J. Zhu, and J. Gao, “Double rulings for information brokerage in sensor networks,” in MOBICOM, 2006. [11] F. Hwang, D. Richards, and P. Winter, “The steiner tree problem,” GI Jahrestagung, vol. 1, no. 2, pp. 370–374, 2003. [12] D. R. Dreyer and M. L. Overton, “Two heuristics for the euclidean steiner tree problem,” Annals of Discrete Mathematics, vol. 53, 1992. [13] M. Diane and J. Plesnik, “Three new heuristics for the steiner problem in graphs,” Acta Math. Univ. Comenianae, vol. 60, pp. 105–121, 1991. [14] T. H. Cormen, C. E. Leiserson, R. L. Rivest, and C. Stein, Introduction to Algorithms, Second Edition. 173 Authorized licensed use limited to: Nanjing University. Downloaded on July 11,2010 at 07:42:17 UTC from IEEE Xplore. Restrictions apply