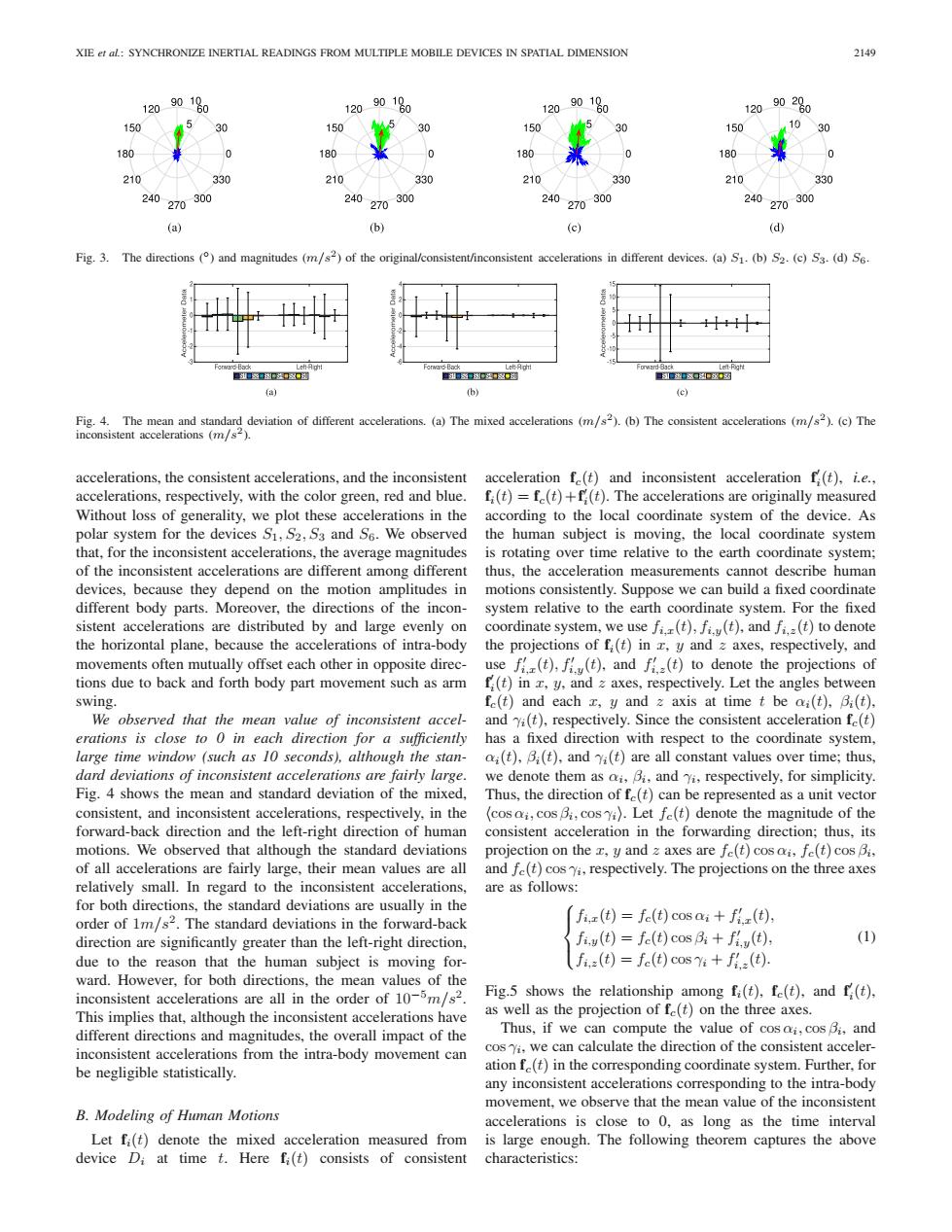
XIE et al:SYNCHRONIZE INERTIAL READINGS FROM MULTIPLE MOBILE DEVICES IN SPATIAL DIMENSION 2149 12090180 120 9010 120 90180 120 902%0 150 30 150 30 150 30 150 10 30 180 180 0 180 180 210 330 210 330 210 330 210 330 240270300 240270300 240270300 240270300 (a b (c) (d) Fig.3.The directions (and magnitudes (m/s2)of the original/consistent/inconsistent accelerations in different devices.(a)S1.(b)S2.(c)S3.(d)56. ■出口多塞法口型 口出强口澳类多口类 口光口器口数图 (2) Fig.4.The mean and standard deviation of different accelerations.(a)The mixed accelerations (m/s2).(b)The consistent accelerations (m/s?).(c)The inconsistent accelerations (m/s). accelerations,the consistent accelerations,and the inconsistent acceleration f(t)and inconsistent acceleration f(t),ie., accelerations,respectively,with the color green,red and blue. fi(t)=fe(t)+f(t).The accelerations are originally measured Without loss of generality,we plot these accelerations in the according to the local coordinate system of the device.As polar system for the devices S1,S2,S3 and S6.We observed the human subject is moving,the local coordinate system that,for the inconsistent accelerations,the average magnitudes is rotating over time relative to the earth coordinate system; of the inconsistent accelerations are different among different thus.the acceleration measurements cannot describe human devices,because they depend on the motion amplitudes in motions consistently.Suppose we can build a fixed coordinate different body parts.Moreover,the directions of the incon- system relative to the earth coordinate system.For the fixed sistent accelerations are distributed by and large evenly on coordinate system,we use fi(t),fi.(t),and fi.=(t)to denote the horizontal plane,because the accelerations of intra-body the projections of fi(t)in y and 2 axes,respectively,and movements often mutually offset each other in opposite direc- use f(t),f(t).and f (t)to denote the projections of tions due to back and forth body part movement such as arm f(t)in y.and z axes,respectively.Let the angles between swing. fe(t)and each x,y and z axis at time t be ai(t).Bi(t). We observed that the mean value of inconsistent accel- and i(t),respectively.Since the consistent acceleration fe(t) erations is close to 0 in each direction for a sufficiently has a fixed direction with respect to the coordinate system, large time window (such as 10 seconds),although the stan- i(t),Bi(t),and (t)are all constant values over time;thus, dard deviations of inconsistent accelerations are fairly large. we denote them as ai,Bi,and i,respectively,for simplicity. Fig.4 shows the mean and standard deviation of the mixed, Thus,the direction of fe(t)can be represented as a unit vector consistent,and inconsistent accelerations,respectively,in the (cos ai,cos Bi,cosYi).Let fe(t)denote the magnitude of the forward-back direction and the left-right direction of human consistent acceleration in the forwarding direction;thus,its motions.We observed that although the standard deviations projection on the y and z axes are fe(t)cos ai,fe(t)cos Bi, of all accelerations are fairly large,their mean values are all and fe(t)cosi,respectively.The projections on the three axes relatively small.In regard to the inconsistent accelerations, are as follows: for both directions.the standard deviations are usually in the order of 1m/s2.The standard deviations in the forward-back fi.r(t)=fe(t)cosai+fir(t), direction are significantly greater than the left-right direction, fi.y(t)=fe(t)cosBi+fi.y(t), (1) due to the reason that the human subject is moving for- fi.z(t)=fe(t)cosvi+fz(t). ward.However.for both directions.the mean values of the inconsistent accelerations are all in the order of 10-5m/s2. Fig.5 shows the relationship among fi(t),fe(t),and f(t), This implies that,although the inconsistent accelerations have as well as the projection of fe(t)on the three axes. different directions and magnitudes,the overall impact of the Thus,if we can compute the value of cos ai,cos Bi,and inconsistent accelerations from the intra-body movement can cos i,we can calculate the direction of the consistent acceler- be negligible statistically. ation f(t)in the corresponding coordinate system.Further,for any inconsistent accelerations corresponding to the intra-body movement,we observe that the mean value of the inconsistent B.Modeling of Human Motions accelerations is close to 0,as long as the time interval Let fi(t)denote the mixed acceleration measured from is large enough.The following theorem captures the above device Di at time t.Here fi(t)consists of consistent characteristics:XIE et al.: SYNCHRONIZE INERTIAL READINGS FROM MULTIPLE MOBILE DEVICES IN SPATIAL DIMENSION 2149 Fig. 3. The directions (◦) and magnitudes (m/s2) of the original/consistent/inconsistent accelerations in different devices. (a) S1. (b) S2. (c) S3. (d) S6. Fig. 4. The mean and standard deviation of different accelerations. (a) The mixed accelerations (m/s2). (b) The consistent accelerations (m/s2). (c) The inconsistent accelerations (m/s2). accelerations, the consistent accelerations, and the inconsistent accelerations, respectively, with the color green, red and blue. Without loss of generality, we plot these accelerations in the polar system for the devices S1, S2, S3 and S6. We observed that, for the inconsistent accelerations, the average magnitudes of the inconsistent accelerations are different among different devices, because they depend on the motion amplitudes in different body parts. Moreover, the directions of the incon￾sistent accelerations are distributed by and large evenly on the horizontal plane, because the accelerations of intra-body movements often mutually offset each other in opposite direc￾tions due to back and forth body part movement such as arm swing. We observed that the mean value of inconsistent accel￾erations is close to 0 in each direction for a sufficiently large time window (such as 10 seconds), although the stan￾dard deviations of inconsistent accelerations are fairly large. Fig. 4 shows the mean and standard deviation of the mixed, consistent, and inconsistent accelerations, respectively, in the forward-back direction and the left-right direction of human motions. We observed that although the standard deviations of all accelerations are fairly large, their mean values are all relatively small. In regard to the inconsistent accelerations, for both directions, the standard deviations are usually in the order of 1m/s2. The standard deviations in the forward-back direction are significantly greater than the left-right direction, due to the reason that the human subject is moving for￾ward. However, for both directions, the mean values of the inconsistent accelerations are all in the order of 10−5m/s2. This implies that, although the inconsistent accelerations have different directions and magnitudes, the overall impact of the inconsistent accelerations from the intra-body movement can be negligible statistically. B. Modeling of Human Motions Let fi(t) denote the mixed acceleration measured from device Di at time t. Here fi(t) consists of consistent acceleration fc(t) and inconsistent acceleration f i(t), i.e., fi(t) = fc(t)+f i(t). The accelerations are originally measured according to the local coordinate system of the device. As the human subject is moving, the local coordinate system is rotating over time relative to the earth coordinate system; thus, the acceleration measurements cannot describe human motions consistently. Suppose we can build a fixed coordinate system relative to the earth coordinate system. For the fixed coordinate system, we use fi,x(t), fi,y(t), and fi,z(t) to denote the projections of fi(t) in x, y and z axes, respectively, and use f i,x(t), f i,y(t), and f i,z(t) to denote the projections of f i(t) in x, y, and z axes, respectively. Let the angles between fc(t) and each x, y and z axis at time t be αi(t), βi(t), and γi(t), respectively. Since the consistent acceleration fc(t) has a fixed direction with respect to the coordinate system, αi(t), βi(t), and γi(t) are all constant values over time; thus, we denote them as αi, βi, and γi, respectively, for simplicity. Thus, the direction of fc(t) can be represented as a unit vector cos αi, cos βi, cos γi. Let fc(t) denote the magnitude of the consistent acceleration in the forwarding direction; thus, its projection on the x, y and z axes are fc(t) cos αi, fc(t) cos βi, and fc(t) cos γi, respectively. The projections on the three axes are as follows: ⎧ ⎪⎨ ⎪⎩ fi,x(t) = fc(t) cos αi + f i,x(t), fi,y(t) = fc(t) cos βi + f i,y(t), fi,z(t) = fc(t) cos γi + f i,z(t). (1) Fig.5 shows the relationship among fi(t), fc(t), and f i(t), as well as the projection of fc(t) on the three axes. Thus, if we can compute the value of cos αi, cos βi, and cos γi, we can calculate the direction of the consistent acceler￾ation fc(t) in the corresponding coordinate system. Further, for any inconsistent accelerations corresponding to the intra-body movement, we observe that the mean value of the inconsistent accelerations is close to 0, as long as the time interval is large enough. The following theorem captures the above characteristics: