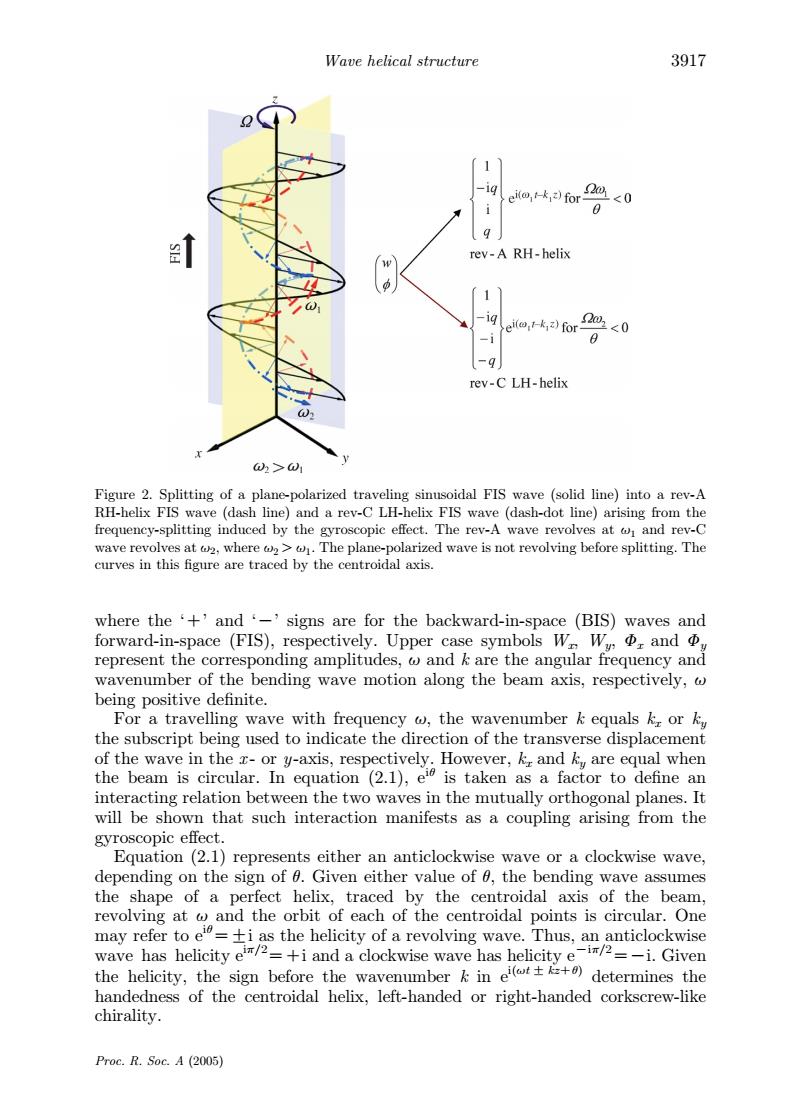
Wave helical structure 3917 11 -ig eil,)for 2<0 i 0 rev-A RH-helix 1】 -ig ei(k)for 2m2<0 -i -9 rev-C LH-helix 2>1 Figure 2.Splitting of a plane-polarized traveling sinusoidal FIS wave (solid line)into a rev-A RH-helix FIS wave (dash line)and a rev-C LH-helix FIS wave (dash-dot line)arising from the frequency-splitting induced by the gyroscopic effect.The rev-A wave revolves at and rev-C wave revolves at w2,where2>.The plane-polarized wave is not revolving before splitting.The curves in this figure are traced by the centroidal axis. where the +and-'signs are for the backward-in-space (BIS)waves and forward-in-space(FIS),respectively.Upper case symbols Wr W,Φ，andΦ， represent the corresponding amplitudes,and k are the angular frequency and wavenumber of the bending wave motion along the beam axis,respectively,@ being positive definite. For a travelling wave with frequency w,the wavenumber k equals k or ky the subscript being used to indicate the direction of the transverse displacement of the wave in the z-or y-axis,respectively.However,k,and ky are equal when the beam is circular.In equation (2.1),ei is taken as a factor to define an interacting relation between the two waves in the mutually orthogonal planes.It will be shown that such interaction manifests as a coupling arising from the gyroscopic effect. Equation(2.1)represents either an anticlockwise wave or a clockwise wave, depending on the sign of 0.Given either value of 6,the bending wave assumes the shape of a perfect helix,traced by the centroidal axis of the beam, revolving at and the orbit of each of the centroidal points is circular.One may refer to e=ti as the helicity of a revolving wave.Thus,an anticlockwise wave has helicity e2=+i and a clockwise wave has helicity e-i/2=-i.Given the helicity,the sign before the wavenumber k in e)determines the handedness of the centroidal helix,left-handed or right-handed corkscrew-like chirality. Proc.R.Soc.A (2005)where the ‘C’ and ‘K’ signs are for the backward-in-space (BIS) waves and forward-in-space (FIS), respectively. Upper case symbols Wx, Wy, Fx and Fy represent the corresponding amplitudes, u and k are the angular frequency and wavenumber of the bending wave motion along the beam axis, respectively, u being positive definite. For a travelling wave with frequency u, the wavenumber k equals kx or ky the subscript being used to indicate the direction of the transverse displacement of the wave in the x - or y-axis, respectively. However, kx and ky are equal when the beam is circular. In equation (2.1), eiq is taken as a factor to define an interacting relation between the two waves in the mutually orthogonal planes. It will be shown that such interaction manifests as a coupling arising from the gyroscopic effect. Equation (2.1) represents either an anticlockwise wave or a clockwise wave, depending on the sign of q. Given either value of q, the bending wave assumes the shape of a perfect helix, traced by the centroidal axis of the beam, revolving at u and the orbit of each of the centroidal points is circular. One may refer to eiq ZGi as the helicity of a revolving wave. Thus, an anticlockwise wave has helicity eip/2ZCi and a clockwise wave has helicity eKip/2ZKi. Given the helicity, the sign before the wavenumber k in ei(ut G kzCq) determines the handedness of the centroidal helix, left-handed or right-handed corkscrew-like chirality. Figure 2. Splitting of a plane-polarized traveling sinusoidal FIS wave (solid line) into a rev-A RH-helix FIS wave (dash line) and a rev-C LH-helix FIS wave (dash-dot line) arising from the frequency-splitting induced by the gyroscopic effect. The rev-A wave revolves at u1 and rev-C wave revolves at u2, where u2Ou1. The plane-polarized wave is not revolving before splitting. The curves in this figure are traced by the centroidal axis. Wave helical structure 3917 Proc. R. Soc. A (2005)