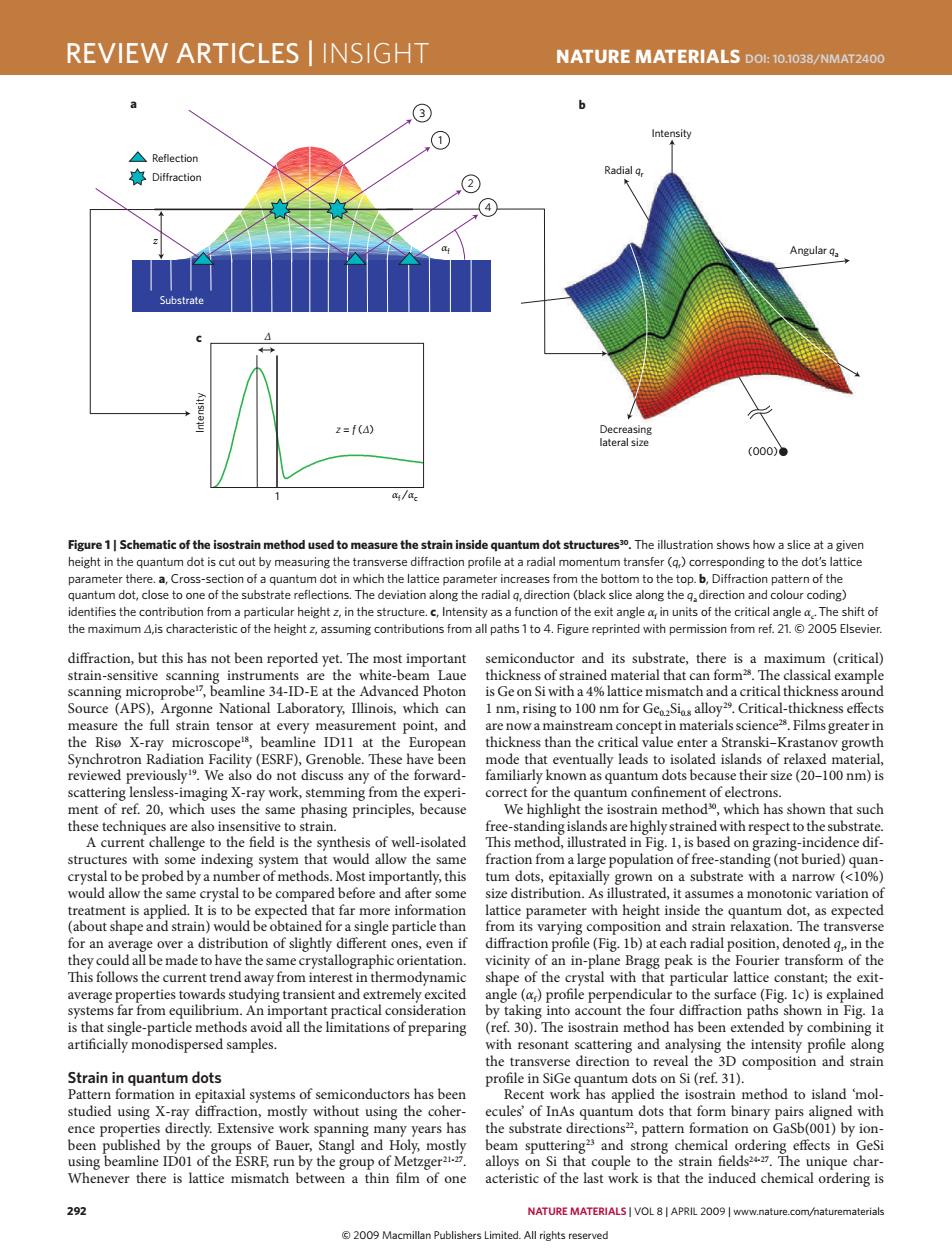
REVIEW ARTICLES INSIGHT NATURE MATERIALS DOL:10.1038/NMAT2400 ③ 1 Intensity △Reflection 赛Diffraction Radial q, 4 Angular qa Substrate 2=f(4) Decreasing lateral size (000)● a/a. Figure 1|Schematic of the isostrain method used to measure the strain inside quantum dot structures3.The illustration shows how a slice at a given height in the quantum dot is cut out by measuring the transverse diffraction profile at a radial momentum transfer (q)corresponding to the dot's lattice parameter there.a,Cross-section of a quantum dot in which the lattice parameter increases from the bottom to the top.b,Diffraction pattern of the quantum dot,close to one of the substrate reflections.The deviation along the radial q,direction (black slice along the g,direction and colour coding) identifies the contribution from a particular height z,in the structure.c,Intensity as a function of the exit angle a,in units of the critical angle a.The shift of the maximum A,is characteristic of the height z,assuming contributions from all paths 1 to 4.Figure reprinted with permission from ref.21.2005 Elsevier. diffraction,but this has not been reported yet.The most important semiconductor and its substrate,there is a maximum (critical) strain-sensitive scanning instruments are the white-beam Laue thickness of strained material that can form2.The classical example scanning microprobe",beamline 34-ID-E at the Advanced Photon is Ge on Si with a 4%lattice mismatch and a critical thickness around Source (APS),Argonne National Laboratory,Illinois,which can 1 nm,rising to 100 nm for GeoSios alloy29.Critical-thickness effects measure the full strain tensor at every measurement point,and are now a mainstream concept in materials science2.Films greater in the Riso X-ray microscope1s,beamline ID11 at the European thickness than the critical value enter a Stranski-Krastanov growth Synchrotron Radiation Facility(ESRF),Grenoble.These have been mode that eventually leads to isolated islands of relaxed material, reviewed previously.We also do not discuss any of the forward- familiarly known as quantum dots because their size(20-100 nm)is scattering lensless-imaging X-ray work,stemming from the experi- correct for the quantum confinement of electrons. ment of ref.20,which uses the same phasing principles,because We highlight the isostrain method,which has shown that such these techniques are also insensitive to strain. free-standing islands are highly strained with respect to the substrate. A current challenge to the field is the synthesis of well-isolated This method,illustrated in Fig.1,is based on grazing-incidence dif- structures with some indexing system that would allow the same fraction from a large population of free-standing(not buried)quan- crystal to be probed by a number of methods.Most importantly,this tum dots,epitaxially grown on a substrate with a narrow (<10%) would allow the same crystal to be compared before and after some size distribution.As illustrated,it assumes a monotonic variation of treatment is applied.It is to be expected that far more information lattice parameter with height inside the quantum dot,as expected (about shape and strain)would be obtained for a single particle than from its varying composition and strain relaxation.The transverse for an average over a distribution of slightly different ones,even if diffraction profile (Fig.1b)at each radial position,denoted g in the they could all be made to have the same crystallographic orientation. vicinity of an in-plane Bragg peak is the Fourier transform of the This follows the current trend away from interest in thermodynamic shape of the crystal with that particular lattice constant;the exit- average properties towards studying transient and extremely excited angle (a)profile perpendicular to the surface (Fig.Ic)is explained systems far from equilibrium.An important practical consideration by taking into account the four diffraction paths shown in Fig.la is that single-particle methods avoid all the limitations of preparing (ref.30).The isostrain method has been extended by combining it artificially monodispersed samples. with resonant scattering and analysing the intensity profile along the transverse direction to reveal the 3D composition and strain Strain in quantum dots profile in SiGe quantum dots on Si (ref.31). Pattern formation in epitaxial systems of semiconductors has been Recent work has applied the isostrain method to island 'mol- studied using X-ray diffraction,mostly without using the coher- ecules'of InAs quantum dots that form binary pairs aligned with ence properties directly.Extensive work spanning many years has the substrate directions2,pattern formation on GaSb(001)by ion- been published by the groups of Bauer,Stangl and Holy,mostly beam sputtering2 and strong chemical ordering effects in GeSi using beamline ID01 of the ESRE,run by the group of Metzger5. alloys on Si that couple to the strain fields2427.The unique char- Whenever there is lattice mismatch between a thin film of one acteristic of the last work is that the induced chemical ordering is 292 NATURE MATERIALS VOL 8|APRIL 2009 www.nature.com/naturematerials 2009 Macmillan Publishers Limited.All rights reserved292 nature materials | VOL 8 | APRIL 2009 | www.nature.com/naturematerials review articles | insight NaTure maTerials doi: 10.1038/nmat2400 diffraction, but this has not been reported yet. The most important strain-sensitive scanning instruments are the white-beam Laue scanning microprobe17, beamline 34-ID-E at the Advanced Photon Source (APS), Argonne National Laboratory, Illinois, which can measure the full strain tensor at every measurement point, and the Risø X-ray microscope18, beamline ID11 at the European Synchrotron Radiation Facility (ESRF), Grenoble. These have been reviewed previously19. We also do not discuss any of the forward￾scattering lensless-imaging X-ray work, stemming from the experi￾ment of ref. 20, which uses the same phasing principles, because these techniques are also insensitive to strain. A current challenge to the field is the synthesis of well-isolated structures with some indexing system that would allow the same crystal to be probed by a number of methods. Most importantly, this would allow the same crystal to be compared before and after some treatment is applied. It is to be expected that far more information (about shape and strain) would be obtained for a single particle than for an average over a distribution of slightly different ones, even if they could all be made to have the same crystallographic orientation. This follows the current trend away from interest in thermodynamic average properties towards studying transient and extremely excited systems far from equilibrium. An important practical consideration is that single-particle methods avoid all the limitations of preparing artificially monodispersed samples. strain in quantum dots Pattern formation in epitaxial systems of semiconductors has been studied using X-ray diffraction, mostly without using the coher￾ence properties directly. Extensive work spanning many years has been published by the groups of Bauer, Stangl and Holy, mostly using beamline ID01 of the ESRF, run by the group of Metzger21-27. Whenever there is lattice mismatch between a thin film of one semiconductor and its substrate, there is a maximum (critical) thickness of strained material that can form28. The classical example is Ge on Si with a 4% lattice mismatch and a critical thickness around 1 nm, rising to 100 nm for Ge0.2Si0.8 alloy29. Critical-thickness effects are now a mainstream concept in materials science28. Films greater in thickness than the critical value enter a Stranski–Krastanov growth mode that eventually leads to isolated islands of relaxed material, familiarly known as quantum dots because their size (20–100 nm) is correct for the quantum confinement of electrons. We highlight the isostrain method30, which has shown that such free-standing islands are highly strained with respect to the substrate. This method, illustrated in Fig. 1, is based on grazing-incidence dif￾fraction from a large population of free-standing (not buried) quan￾tum dots, epitaxially grown on a substrate with a narrow (<10%) size distribution. As illustrated, it assumes a monotonic variation of lattice parameter with height inside the quantum dot, as expected from its varying composition and strain relaxation. The transverse diffraction profile (Fig. 1b) at each radial position, denoted qr , in the vicinity of an in-plane Bragg peak is the Fourier transform of the shape of the crystal with that particular lattice constant; the exit￾angle (αf) profile perpendicular to the surface (Fig. 1c) is explained by taking into account the four diffraction paths shown in Fig. 1a (ref. 30). The isostrain method has been extended by combining it with resonant scattering and analysing the intensity profile along the transverse direction to reveal the 3D composition and strain profile in SiGe quantum dots on Si (ref. 31). Recent work has applied the isostrain method to island ‘mol￾ecules’ of InAs quantum dots that form binary pairs aligned with the substrate directions22, pattern formation on GaSb(001) by ion￾beam sputtering23 and strong chemical ordering effects in GeSi alloys on Si that couple to the strain fields24-27. The unique char￾acteristic of the last work is that the induced chemical ordering is z 3 1 2 Substrate Reflection Diraction (000) Decreasing lateral size Intensity 1 Intensity a b c Angular qa Radial qr αf /αc z = f (Δ) Δ αf 4 Figure 1 | schematic of the isostrain method used to measure the strain inside quantum dot structures30. The illustration shows how a slice at a given height in the quantum dot is cut out by measuring the transverse diffraction profile at a radial momentum transfer (qr ) corresponding to the dot’s lattice parameter there. a, Cross-section of a quantum dot in which the lattice parameter increases from the bottom to the top. b, Diffraction pattern of the quantum dot, close to one of the substrate reflections. The deviation along the radial qr direction (black slice along the qa direction and colour coding) identifies the contribution from a particular height z, in the structure. c, Intensity as a function of the exit angle αf in units of the critical angle αc.The shift of the maximum Δ,is characteristic of the height z, assuming contributions from all paths 1 to 4. Figure reprinted with permission from ref. 21. © 2005 Elsevier. nmat_2400_APR09.indd 292 13/3/09 12:04:28 © 2009 Macmillan Publishers Limited. All rights reserved