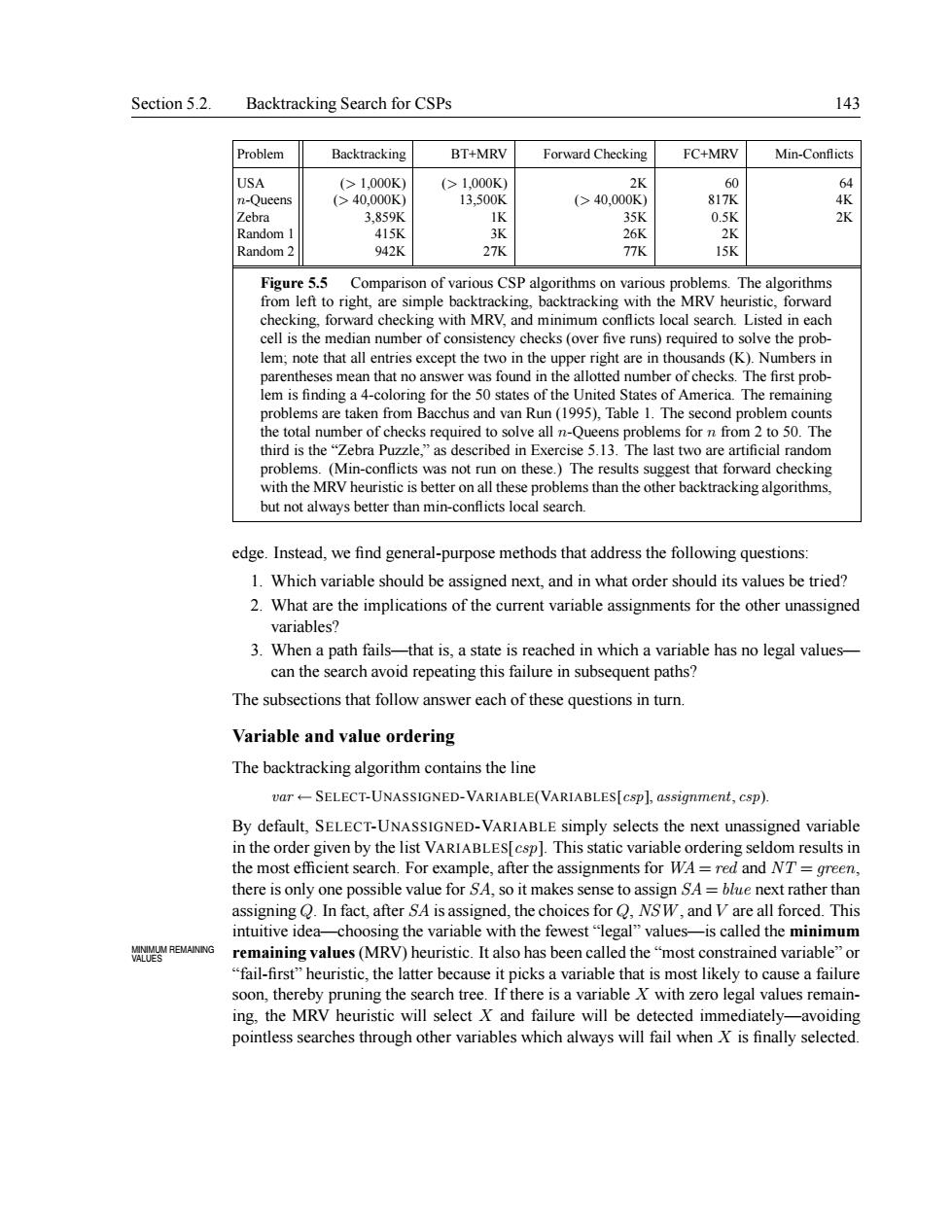
Section 5.2. Backtracking Search for CSPs 143 Problem Backtracking BT+MRV Forward Checking FC+MRY Min-Conflicts (000 6 817 415 Random 2 942K 27K 77K 15K Figure 5.5 o right re simple orwa cell is the median number of consistenc checks (over five runs)required to solve the p lem;note that all entries except the two in the upper right are in thousands(K).Numbers in parentheses mean that no answer was found in the allotted number of checks.The first prob em is finding a ne 3 /1005 the total number of checks required to solve all n-Que problems for from 2 to 50 The third is the"Zebra Puzzle,"as described in Exercise 5.13.The last two are artificial random was not run on thes han the rward checking ot alwa edge.Instead,we find general-purpose methods that address the following questions: 1.Which variable should be assigned next,and in what order should its values be tried? 2.What are the implications of the current variable assignments for the other unassigned variables? 3.When a path fails-that is,a state is reached in which a variable has no legal values- can the search avoid repeating this failure in subsequent paths? The subsections that follow answer each of these questions in turn. Variable and value ordering The backtracking algorithm contains the line var+-SELECT-UNASSIGNED-VARIABLE(VARIABLES[csp],assignment,csp). By default,SELECT-UNASSIGNED-VARIABLE simply selects the next unassigned variable in the order given by the list VARIABLES[csp].This static variable ordering seldom results in the most efficient search.For example,after the assignments for WA=red and NT=green, there is only one possible value for SA,so it makes sense to assign SA=blue next rather than assigning Q.In fact,after SA is assigned,the choices for Q,NSW,and V are all forced.This intuitive idea-choosing the variable with the fewest"legal"values-is called the minimum remaining values(MRV)heuristic.It also has been called the"most constrained variable"or "fail-first"heuristic,the latter because it picks a variable that is most likely to cause a failure soon,thereby pruning the search tree.If there is a variable X with zero legal values remain- ing.the MRV heuristic will select X and failure will be detected immediately-avoiding pointless searches through other variables which always will fail when X is finally selected Section 5.2. Backtracking Search for CSPs 143 Problem Backtracking BT+MRV Forward Checking FC+MRV Min-Conflicts USA (> 1,000K) (> 1,000K) 2K 60 64 n-Queens (> 40,000K) 13,500K (> 40,000K) 817K 4K Zebra 3,859K 1K 35K 0.5K 2K Random 1 415K 3K 26K 2K Random 2 942K 27K 77K 15K Figure 5.5 Comparison of various CSP algorithms on various problems. The algorithms from left to right, are simple backtracking, backtracking with the MRV heuristic, forward checking, forward checking with MRV, and minimum conflicts local search. Listed in each cell is the median number of consistency checks (over five runs) required to solve the prob￾lem; note that all entries except the two in the upper right are in thousands (K). Numbers in parentheses mean that no answer was found in the allotted number of checks. The first prob￾lem is finding a 4-coloring for the 50 states of the United States of America. The remaining problems are taken from Bacchus and van Run (1995), Table 1. The second problem counts the total number of checks required to solve all n-Queens problems for n from 2 to 50. The third is the “Zebra Puzzle,” as described in Exercise 5.13. The last two are artificial random problems. (Min-conflicts was not run on these.) The results suggest that forward checking with the MRV heuristic is better on all these problems than the other backtracking algorithms, but not always better than min-conflicts local search. edge. Instead, we find general-purpose methods that address the following questions: 1. Which variable should be assigned next, and in what order should its values be tried? 2. What are the implications of the current variable assignments for the other unassigned variables? 3. When a path fails—that is, a state is reached in which a variable has no legal values— can the search avoid repeating this failure in subsequent paths? The subsections that follow answer each of these questions in turn. Variable and value ordering The backtracking algorithm contains the line var ← SELECT-UNASSIGNED-VARIABLE(VARIABLES[csp], assignment, csp). By default, SELECT-UNASSIGNED-VARIABLE simply selects the next unassigned variable in the order given by the list VARIABLES[csp]. This static variable ordering seldom results in the most efficient search. For example, after the assignments for WA = red and NT = green, there is only one possible value for SA, so it makes sense to assign SA = blue next rather than assigning Q. In fact, after SA is assigned, the choices for Q, NSW , and V are all forced. This intuitive idea—choosing the variable with the fewest “legal” values—is called the minimum remaining values (MRV) heuristic. It also has been called the “most constrained variable” or MINIMUM REMAINING VALUES “fail-first” heuristic, the latter because it picks a variable that is most likely to cause a failure soon, thereby pruning the search tree. If there is a variable X with zero legal values remain￾ing, the MRV heuristic will select X and failure will be detected immediately—avoiding pointless searches through other variables which always will fail when X is finally selected