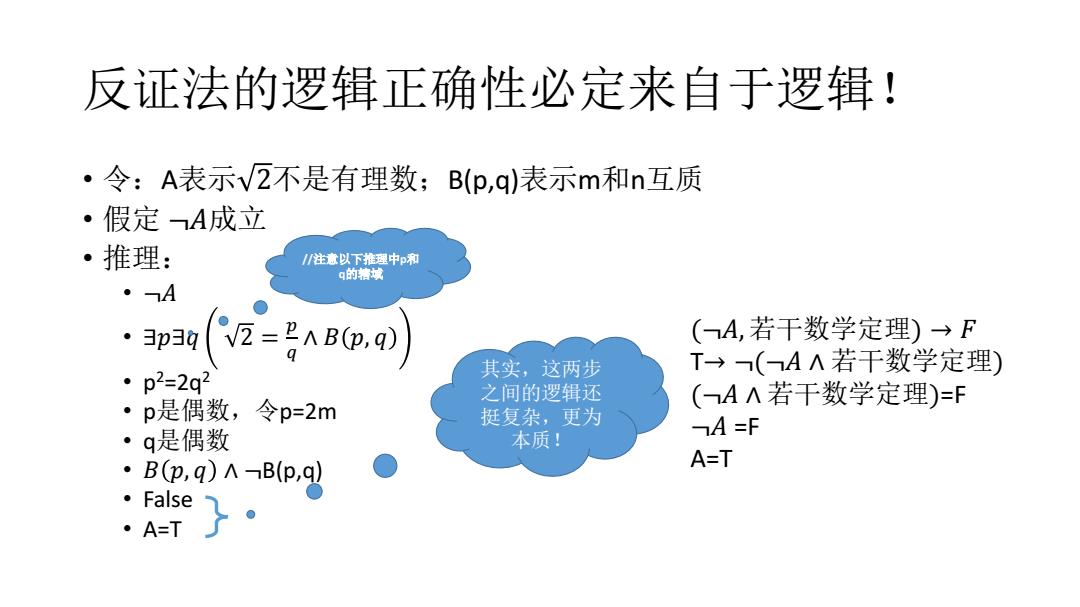
反证法的逻辑正确性必定来自于逻辑！ ·令：A表示V2不是有理数；B(p,q)表示m和n互质 ·假定A成立 ·推理： /注意以下推理中p和 q的精域 ·A ·3p30 VZ=2AB(p.q) (A,若干数学定理)→F 其实，这两步 T→(AA若干数学定理) ·p2=2q2 之间的逻辑还 ·p是偶数， (A∧若干数学定理)=F 令p=2m 挺复杂，更为 ·q是偶数 本质！ A=F ·B(p,q)Bp,y A=T 。False ·A=T }·反证法的逻辑正确性必定来自于逻辑！ • 令：A表示 2不是有理数；B(p,q)表示m和n互质 • 假定 ¬𝐴成立 • 推理： • ¬𝐴 • ∃𝑝∃𝑞 2 = 𝑝 𝑞 ∧ 𝐵 𝑝, 𝑞 • p 2=2q2 • p是偶数，令p=2m • q是偶数 • 𝐵 𝑝, 𝑞 ∧ ¬B(p,q) • False • A=T (¬𝐴,若干数学定理) → 𝐹 T→ ¬(¬𝐴 ∧ 若干数学定理) (¬𝐴 ∧ 若干数学定理)=F ¬𝐴 =F A=T //注意以下推理中p和 q的辖域 其实，这两步 之间的逻辑还 挺复杂，更为 本质！